标签：more ast serve mat sequence possible pushd kth mit
题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1890
Time Limit: 6000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
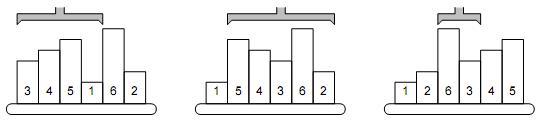
题意：
给出一个n，给出n个样品的高度，
给出一种根据高度排序的算法，其第 i 次操作：找到第 i 小的那个数的位置为Pi，将整个区间[i,Pi]反转，这样一来第 i 小的数就在位置 i 上；从 i 等于 1 到 n 循环这样的操作。
现在要求你给出每次操作的Pi。
题解：
伸展树1~n建树，把每个节点key值等于节点的编号（即key[x] = x），同时使得中序遍历伸展树得到的序列为1~n，
以题目中两个样例为例，建成的树应为如下图：
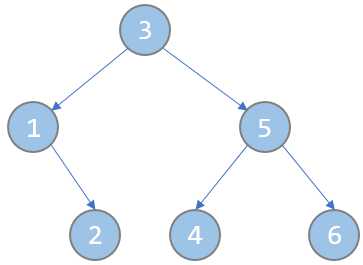
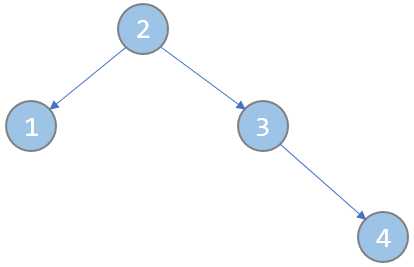（注意，图中节点内的数字，既是节点编号，也是key值，即key[3] = 3，key[1] = 1，key[5] = 5……）
我们此时的伸展树维护的是n个样品的编号（编号为1~n）；
将n个样品按输入顺序编号，再按照first高度second编号进行升序排序，那么新的顺序，就是题目中所描述的排序算法中的每次操作的顺序，
这样，按新的顺序依次枚举n个样品，对于第 i 个样品，其编号为sample[i].id，
我们此时就要去伸展树中寻找某个节点x，其key[x] = sample[i].id；而我们要求的Pi，就是比这个节点小的节点个数加1；
根据上面反复提到的，key[x] = x，所以我们其实就是把节点x = sample[i].id伸展到根，然后求其左子树内节点个数，再加1，
同时，因为需要区间翻转，所以我们可以翻转左子树，并且删除根节点，相当于翻转了[i,Pi]，
由于我们不断的删除节点，因此实际答案就应该是左子树内节点个数 + 1 + (i - 1)。
AC代码：
#include<bits/stdc++.h> #define Key_value ch[ch[root][1]][0] using namespace std; const int maxn=1e5+10; int n; struct Sample { int h; int id; }sample[maxn]; bool cmp(Sample a,Sample b) { if(a.h==b.h) return a.id<b.id; else return a.h<b.h; } /******************************** splay - st ********************************/ int root,nodecnt; int par[maxn],ch[maxn][2]; int key[maxn],size[maxn]; bool rev[maxn]; void NewNode(int &x,int p,int k) { x=k; par[x]=p; ch[x][0]=ch[x][1]=0; key[x]=k; size[x]=1; rev[x]=0; } void Update_Rev(int x) { if(x==0) return; rev[x]=!rev[x]; } void Pushup(int x) { size[x]=size[ch[x][0]]+size[ch[x][1]]+1; } void Pushdown(int x) { if(rev[x]) { swap(ch[x][0],ch[x][1]); rev[ch[x][0]]^=1; rev[ch[x][1]]^=1; rev[x]=0; } } void Rotate(int x,int type) //旋转，0为左旋zag，1为右旋zig { int y=par[x]; Pushdown(y); Pushdown(x); //先把y的标记向下传递,再把x的标记往下传递 ch[y][!type]=ch[x][type]; par[ch[x][type]]=y; if(par[y]) ch[par[y]][(ch[par[y]][1]==y)]=x; par[x]=par[y]; ch[x][type]=y; par[y]=x; Pushup(y); Pushup(x); } void Splay(int x,int goal) { Pushdown(x); while(par[x]!=goal) { if(par[par[x]]==goal) { Pushdown(par[x]); Pushdown(x); Rotate(x,ch[par[x]][0]==x); //左孩子zig，有孩子zag } else { Pushdown(par[par[x]]); Pushdown(par[x]); Pushdown(x); int y=par[x]; int type=(ch[par[y]][0]==y); //type=0，y是右孩子；type=1，y是左孩子 if(ch[y][type]==x) { Rotate(x,!type); Rotate(x,type); } else { Rotate(y,type); Rotate(x,type); } } } if(goal==0) root=x; } int Get_Kth(int x,int k) //得到第k个节点 { Pushdown(x); int t=size[ch[x][0]]+1; if(t==k) return x; if(t>k) return Get_Kth(ch[x][0],k); else return Get_Kth(ch[x][1],k-t); } int Get_Min(int x) { Pushdown(x); while(ch[x][0]) { x=ch[x][0]; Pushdown(x); } return x; } int Get_Max(int x) { Pushdown(x); while(ch[x][1]) { x=ch[x][1]; Pushdown(x); } return x; } void Build(int &x,int l,int r,int par) { if(l>r) return; int mid=(l+r)/2; NewNode(x,par,mid); Build(ch[x][0],l,mid-1,x); Build(ch[x][1],mid+1,r,x); Pushup(x); } void Init() { root=nodecnt=0; ch[root][0]=ch[root][1]=size[root]=key[root]=par[root]=rev[root]=0; Build(root,1,n,0); } void Del() { if(ch[root][0]==0 && ch[root][1]==0) root=0; else if(ch[root][0]==0) { par[ch[root][1]]=0; root=ch[root][1]; } else if(ch[root][1]==0) { par[ch[root][0]]=0; root=ch[root][0]; } else { int pre=Get_Max(ch[root][0]); int nxt=Get_Min(ch[root][1]); Splay(pre,0); Splay(nxt,root); par[Key_value]=0; Key_value=0; Pushup(ch[root][1]); Pushup(root); } } /******************************** splay - ed ********************************/ int main() { while(scanf("%d",&n) && n!=0) { Init(); for(int i=1;i<=n;i++) { scanf("%d",&sample[i].h); sample[i].id=i; } sort(sample+1,sample+n+1,cmp); for(int i=1;i<n;i++) { Splay(sample[i].id,0); printf("%d ",i+size[ch[root][0]]); Update_Rev(ch[root][0]); Del(); } printf("%d\n",n); } }
HDU 1890 - Robotic Sort - [splay][区间反转+删除根节点]
标签：more ast serve mat sequence possible pushd kth mit
原文地址：https://www.cnblogs.com/dilthey/p/9400506.html
