标签：方式 不同 实验 范围 结束 而不是 随机选择 距离 返回
随机游走模型由首先由爱因斯坦在1926年以数学方式描述。由于自然界中的许多实体会以不可预知的方式移动，因此随机游走模型用来描述这种不稳定的移动。在这种移动模型中，移动节点随机选择一个方向和速度来从当前位置移动到新的位置。新的速度和方向分别从预定义的范围【speedmin，speedmax】和【0，2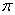
】。移动节点的每次移动会以恒定的时间间隔t或恒定的行进距离d进行，结束后会计算新的方向和速度。如果此模型的移动节点到达模拟边界，则它将从模拟边界“弹回”，其角度有入射方向确定，然后沿着这条路径继续移动。
许多随机游走模型已经被研究，包括一维，二维，三维和d-维游走。在1921年，Polya证明在一维或二维的随机游走能够完全确定地返回远点，这一特征确保随机游走模型代表了一种移动模型----可以测试移动节点在其起点附近的移动，不用担心移动节点因游走而永远回不到起点。
二维随机游走模型是热点。下图显示了一个二维随机游走模型的仿真例子。移动节点在300*600的模拟区域从起点（150,300）移动。在每个拐点，移动节点随机选择【0，2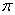】的方向，选择【0，10】m/s的速度。在改变方向与速度之前，移动节点移动60秒。在随机游走模型中，移动节点可以在行进指定距离之后改变方向而不是指定时间。图1的移动节点在改变方向和速度之前总共行进10步（而不是60秒），与图一不同，图二的每次移动都是完全相同的聚类。
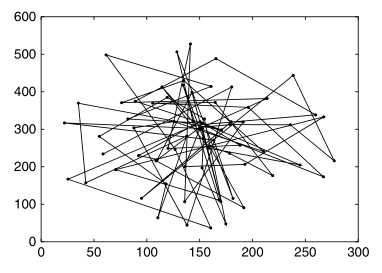
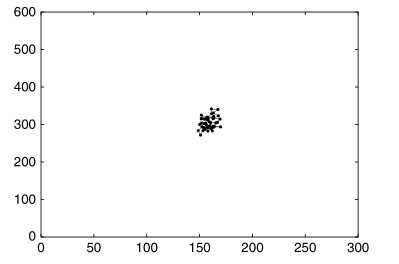
随机游走模型有时被称为布朗运动。在使用模型时，可以简化，Basagni等人在模拟实验中，为每个移动节点分配相同的速度，简化随机游走模型。
标签：方式 不同 实验 范围 结束 而不是 随机选择 距离 返回
原文地址：https://www.cnblogs.com/bjut-lqq/p/9402368.html
