标签:include preview hat spec cst each names lines output
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 474 Accepted Submission(s): 202
for (int i = 0; ; ++i) {
for (int j = 0; j <= i; ++j) {
M[j][i - j] = A[cursor];
cursor = (cursor + 1) % L;
}
}

我们可以发现它是有矩阵周期的,把偶数和奇数的情况都打一遍,发现奇数的时候是以n为一个周期,偶数是2*n
那既然后面的都是相同的,那么我们就没必要构造出来,a数组最大长度是10,所以我们循环矩阵最大是20*20,我们只要把
循环矩阵计算出来即可,后面的相同的不再重复计算,当我们输入一个区间的时候,我们只要算边界和里面循环矩阵的个数即可
这里我们再用到一个二维前缀和来优化我们的时间
b[i][j] 代表i行j列的矩阵的和
二维前缀和这里就不再讲述,我说下怎么由我们的循环矩阵的前缀和延伸到总的大矩阵的前缀和
我们要计算 x y的矩阵前缀和,我们只知道循环矩阵,那我们现在来计算
‘我们3*3的循环矩阵,我们要求5*5的前缀和
我们首先计算出里面包括了多少个循环矩阵
b[n-1][n-1]*(x/n)*(y/n)
b[n-1][n-1]是我们的循环矩阵和,(x/n)代表我的行区间有多少个,(y/n)代表列区间有多少个,乘起来就是总共的了
然后我们计算循环矩阵后,我们要来计算多余的边界
但是他是循环矩阵,所以我们只要进行取模n就能把坐标映射到循环矩阵上
所以行和列都是同理,都还要分别乘以(x/n)和(y/n)
而我们还剩下一个对角,对角可以直接计算,不用除,
看下图
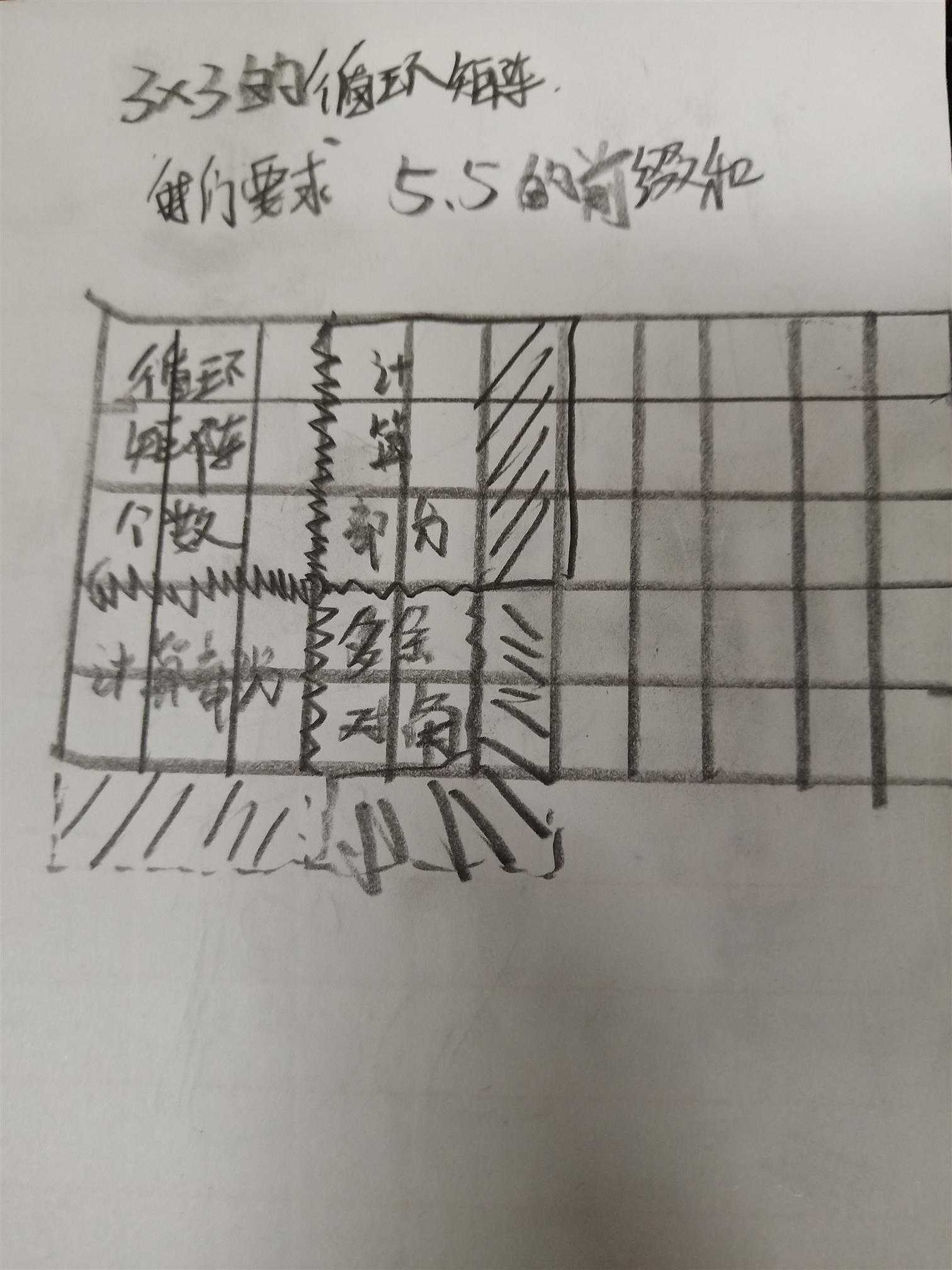
详细解释看代码
#include<cstdio> #include<cstring> #include<cmath> using namespace std; typedef long long ll; ll a[11]; ll b[50][50]; int n,m; ll cal(int x,int y) { if(x<0||y<0) return 0; return b[n-1][n-1]*(x/n)*(y/n)+b[x%n][n-1]*(y/n)+b[n-1][y%n]*(x/n)+b[x%n][y%n];//计算循环矩阵的个数 列的多余边界 行的多余边界 对角的多余边界 } int main() { int t; scanf("%d",&t); while(t--) { scanf("%d",&n); for(int i=0;i<n;i++) scanf("%lld",&a[i]); int cursor = 0; for (int i = 0; i<=45; ++i) {//填充我们的矩阵 for (int j = 0; j <= i; ++j) { b[j][i - j] = a[cursor]; cursor = (cursor + 1) % n; } } n=2*n; for(int i=0;i<n;i++)//计算循环矩阵的二维前缀和 { for(int j=0;j<n;j++) { if(i) b[i][j]+=b[i-1][j]; if(j) b[i][j]+=b[i][j-1]; if(i&&j) b[i][j]-=b[i-1][j-1]; } } int x1,x2,y1,y2; scanf("%d",&m); while(m--) { scanf("%d%d%d%d",&x1,&y1,&x2,&y2); printf("%lld\n",cal(x2,y2)-cal(x2,y1-1)-cal(x1-1,y2)+cal(x1-1,y1-1));//二维前缀和的计算方法(用前缀大矩阵分别减去行列矩阵,但是行列中间重复了一个小矩阵,需要再加上) } } }
标签:include preview hat spec cst each names lines output
原文地址:https://www.cnblogs.com/Lis-/p/9404715.html