标签：ace   spfa算法   很多   get   ems   顶点   https   优化算法   题目   

图论专题训练

已完成

• [x] A
• [x] B
• [x] C

A

• 题意：
  一个国家里有很多个城市，某件物品在所有城市的价格都不同，你可以在一个城市买，另一个城市卖出来获得利益，但是只能进行一次买卖。然后要从1走到n，1到n有单向，也有双向的。
• 题解：将图分层。邻接表，spfa求出最长路（最大权值）。有三层，一层是不购买也不卖，第二层是买，一到第二层的边权为负。第三层是卖，二到第三层的边权为正。由于有向边的建立，你不能从第二/三层走回第一层图，这保证了你只做一次买卖，而不是无限做买卖。然后再设置一个最终大终点。
• 其实这题还有很多方法 参考https://www.luogu.org/problemnew/solution/P1073
  

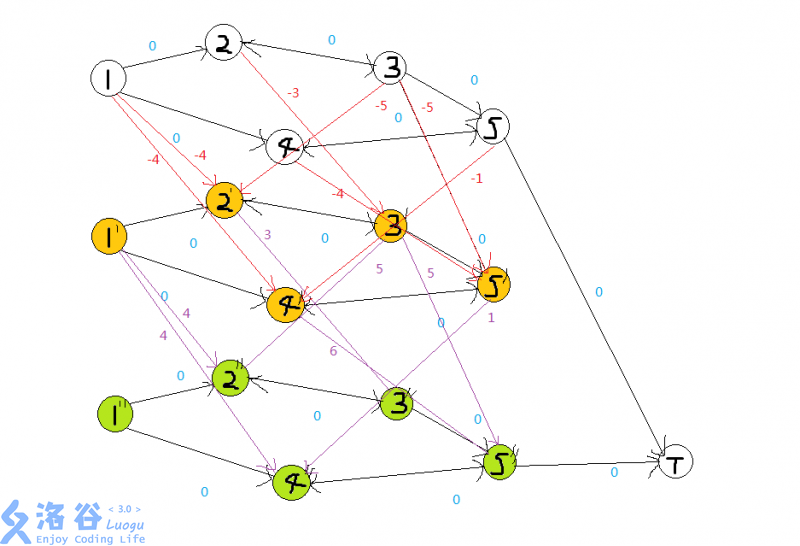
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll mod=1e9+7;
const ll maxn=1e5+7;
const ll inf=1<<18;
struct u
{
    int v,len;
};
int n,m,v[maxn],d[maxn*3+1];
vector<u> vt[maxn*3+1];//邻接表
template<class T>
void read(T &res)
{
    res = 0;
    char c = getchar();
    T f = 1;
    while(c < '0' || c > '9')
    {
        if(c == '-') f = -1;
        c = getchar();
    }
    while(c >= '0' && c <= '9')
    {
        res = res * 10 + c - '0';
        c = getchar();
    }
    res *= f;
}
template<class T>
void out(T x)
{
    if(x < 0)
    {
        putchar('-');
        x = -x;
    }
    if(x >= 10)
    {
        out(x / 10);
    }
    putchar('0' + x % 10);
}
queue<int>Q;
bool inq[maxn*3+1];
void add(int x,int y)
{
     vt[x].push_back((u){y,0});
     vt[x+n].push_back((u){y+n,0});
     vt[x+2*n].push_back((u){y+2*n,0});
     vt[x].push_back((u){y+n,-v[x]});
     vt[x+n].push_back((u){y+2*n,v[x]});
     return;
}
void spfa()
{
    for(int i=1;i<=n;i++) d[i]=-inf;
    d[1]=0;
    inq[1]=true;
    Q.push(1);
    while(!Q.empty())
    {
        int tp=Q.front();
        Q.pop();
        inq[tp]=0;
        int len=vt[tp].size();
        for(int i=0;i<len;i++){
            u x=vt[tp][i];
            if(d[x.v]<d[tp]+x.len){
                d[x.v]=d[tp]+x.len;
                if(inq[x.v]==0){
                    Q.push(x.v);
                    inq[x.v]=1;
                }
            }
        }
    }
}
void init()
{
    read(n);
    read(m);
    for(int i=1;i<=n;i++) read(v[i]);
    for(int i=1,x,y,z;i<=m;i++){
        read(x);
        read(y);
        read(z);
        add(x,y);
        if(z==2) add(y,x);
    }
    vt[n].push_back((u){3*n+1,0});
    vt[n*3].push_back((u){n*3+1,0});
    n=3*n+1;
}
int main()
{
    init();
    spfa();
    out(d[n]);
    printf("\n");
    return 0;
}

这里用到了spfa算法 Bellman-Ford 算法的队列优化 可以判断负权边。

B

• 题意:公路是双向的，航线是单向的，但是航线的花费可能是负的。给定一个起点，求该起点到每个点的最小花费。并且注意不存在那种公路过去又从公路回来坐航线的SB情况。
• 题解：看上去是一个比较标准的最短路，只是有负边。正解是分开来对每个连通块内做dijkstra 然后外面对于连通块用拓扑序， 细节挺多，而且我不会然后这题可以用spfa来做，朴素的spfa会T，可以用双端队列来优化。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll mod=1e9+7;
const ll maxn=80010;
const int inf=0x3f3f3f;
int t,r,p,s;
int d[maxn];
template<class T>
void read(T &res)
{
    res = 0;
    char c = getchar();
    T f = 1;
    while(c < '0' || c > '9')
    {
        if(c == '-') f = -1;
        c = getchar();
    }
    while(c >= '0' && c <= '9')
    {
        res = res * 10 + c - '0';
        c = getchar();
    }
    res *= f;
}
template<class T>
void out(T x)
{
    if(x < 0)
    {
        putchar('-');
        x = -x;
    }
    if(x >= 10)
    {
        out(x / 10);
    }
    putchar('0' + x % 10);
}
struct edge
{
    int v;
    int cost;
    edge(int _v=0,int _cost=0):v(_v),cost(_cost){}
};
vector<edge>e[maxn];
void add(int u,int v,int val)
{
    e[u].push_back(edge(v,val));
}
bool vis[maxn];
int cnt[maxn];
int dist[maxn];
void init()
{
    read(t);
    read(r);
    read(p);
    read(s);
    for(int i=1,a,b,c;i<=r;i++){
        read(a);
        read(b);
        read(c);
        add(a,b,c);
        add(b,a,c);
    }
    for(int i=1,a,b,c;i<=p;i++){
        read(a);
        read(b);
        read(c);
        add(a,b,c);
    }
    for(int i=1;i<=t;i++) d[i]=inf;
}
void spfa()
{
    vis[s]=1;
    d[s]=0;
    deque<int>q;
    q.push_front(s);
    memset(cnt,0,sizeof(cnt));
    cnt[s]=1;
    while(!q.empty())
    {
        int u=q.front();
        q.pop_front();
        vis[u]=0;
        for(int i=0;i<e[u].size();i++){
            int v=e[u][i].v;
            if(d[v]>d[u]+e[u][i].cost){
                d[v]=d[u]+e[u][i].cost;
                if(!vis[v]){
                    vis[v]=true;
                    if(!q.empty()){//SLF优化
                        if(d[v]<d[q.front()]) q.push_front(v);
                        else q.push_back(v);
                    }
                    else q.push_back(v);
                }
            }
        }
    }
}
int main()
{
    init();
    spfa();
    for(int i=1;i<=t;i++){
        if(d[i]>=inf)printf("NO PATH\n");
        else printf("%d\n",d[i]);
    }
    return 0;
}

SPFA算法有两个优化算法 SLF 和 LLL：
SLF：Small Label First 策略，设要加入的节点是j，队首元素为i，若dist(j)<dist(i)，则将j插入队首，否则插入队尾。
LLL：Large Label Last 策略，设队首元素为i，队列中所有dist值的平均值为x，若dist(i)>x则将i插入到队尾，查找下一元素，直到找到某一i使得dist(i)<=x，则将i出对进行松弛操作。 SLF 可使速度提高 15 ~ 20%；SLF + LLL 可提高约 50%.
在实际的应用中SPFA的算法时间效率不是很稳定，为了避免最坏情况的出现，通常使用效率更加稳定的Dijkstra算法。

C

• 题意：
  n个牛做接力运动，t条道路，起点为s，终点为e，求s->e经过n条边的最短路。
• 题解：
  我们先假设n等于2，相当于从起点到终点要经历一个断点k，这可以联想到floyd算法。先铺垫一下，(从零开始)

路径矩阵
通过一个图的权值矩阵求出它的每两点间的最短路径矩阵。
从图的带权邻接矩阵A=[a(i,j)] n×n开始，递归地进行n次更新，即由矩阵D(0)=A，按一个公式，构造出矩阵D(1)；又用同样地公式由D(1)构造出D(2)；……；最后又用同样的公式由D(n-1)构造出矩阵D(n)。矩阵D(n)的i行j列元素便是i号顶点到j号顶点的最短路径长度，称D(n)为图的距离矩阵，同时还可引入一个后继节点矩阵path来记录两点间的最短路径。
采用松弛技术（松弛操作），对在i和j之间的所有其他点进行一次松弛。所以时间复杂度为O(n^3);
状态转移方程
其状态转移方程如下： map[i,j]:=min{map[i,k]+map[k,j],map[i,j]}；
map[i,j]表示i到j的最短距离，K是穷举i,j的断点，map[n,n]初值应该为0，或者按照题目意思来做。
当然，如果这条路没有通的话，还必须特殊处理，比如没有map[i,k]这条路。

由此可见，floyd有种矩阵的思想在里面。那当k>1时该怎么办？
参考国家队集训论文 08年的 矩阵乘法在信息学中的应用
++01邻接矩阵A的K次方C=A^K,C[i][j]表示i点到j点正好经过K条边的路径数++
对应于这道题,对邻接图进行K次floyd之后,C[i][j]就是点i到j正好经过K条边的最短路
进行k次floyd的话复杂度太大，我们可以发现，floyd算法有点像矩阵的乘法，我们可以采用矩阵快速幂来做。
这题可以用map来离散化

#include <bits/stdc++.h>
#define ll long long
using namespace std;
int n,t,s,e,num;
map<int,int>mp;
template<class T>
void read(T &res)
{
    res = 0;
    char c = getchar();
    T f = 1;
    while(c < '0' || c > '9')
    {
        if(c == '-') f = -1;
        c = getchar();
    }
    while(c >= '0' && c <= '9')
    {
        res = res * 10 + c - '0';
        c = getchar();
    }
    res *= f;
}
template<class T>
void out(T x)
{
    if(x < 0)
    {
        putchar('-');
        x = -x;
    }
    if(x >= 10)
    {
        out(x / 10);
    }
    putchar('0' + x % 10);
}
struct matrix
{
    int mapp[210][210];
    matrix(){
        memset(mapp,0x3f,sizeof(mapp));
    }
};
matrix floyd(matrix a,matrix b)
{
    matrix temp;
    int i,j,k;
    for(k=1;k<=num;k++){
        for(i=1;i<=num;i++){
            for(j=1;j<=num;j++){
                if(temp.mapp[i][j]>a.mapp[i][k]+b.mapp[k][j]){
                    temp.mapp[i][j]=a.mapp[i][k]+b.mapp[k][j];
                }
            }
        }
    }
    return temp;
}
matrix solve(matrix a,int k)
{
    matrix ans=a;
    while(k){
        if(k&1){
            ans=floyd(ans,a);
        }
        a=floyd(a,a);
        k>>=1;
    }
    return ans;
}
int main()
{
    matrix a;
    while(~scanf("%d%d%d%d",&n,&t,&s,&e)){
        num=0;
        mp.clear();
        int u,v,w;
        while(t--){
            read(w);
            read(u);
            read(v);
            if(mp[u]==0) mp[u]=++num;
            if(mp[v]==0) mp[v]=++num;
            if(a.mapp[mp[u]][mp[v]]>w)
                a.mapp[mp[u]][mp[v]]=a.mapp[mp[v]][mp[u]]=w;
        }
        a=solve(a,n-1);
        out(a.mapp[mp[s]][mp[e]]);
    }
    return 0;
}

图论专题训练 （更新中）

标签：ace   spfa算法   很多   get   ems   顶点   https   优化算法   题目   

原文地址：https://www.cnblogs.com/smallocean/p/9413337.html