[思维]Finite Encyclopedia of Integer Sequences

标签：time 图片分享图片 number nbsp data seq list 技术分享

题目描述

In Finite Encyclopedia of Integer Sequences (FEIS), all integer sequences of lengths between 1 and N (inclusive) consisting of integers between 1 and K (inclusive) are listed.
Let the total number of sequences listed in FEIS be X. Among those sequences, find the (X⁄2)-th (rounded up to the nearest integer) lexicographically smallest one.

Constraints
1≤N,K≤3×10⁵
N and K are integers.

输入

Input is given from Standard Input in the following format:
K N

输出

Print the (X⁄2)-th (rounded up to the nearest integer) lexicographically smallest sequence listed in FEIS, with spaces in between, where X is the total number of sequences listed in FEIS.

样例输入

3 2

样例输出

2 1

提示

There are 12 sequences listed in FEIS: (1),(1,1),(1,2),(1,3),(2),(2,1),(2,2),(2,3),(3),(3,1),(3,2),(3,3). The (12⁄2=6)-th lexicographically smallest one among them is (2,1).

思路：1.k为偶时：因为序列总数x=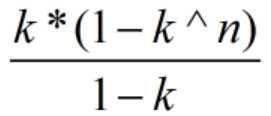，那(X⁄2)-th (rounded up to the nearest integer) lexicographically smallest sequence一定是{k/2,k,k,k...}

2.k为奇时：可以证明(不贴了)，(X⁄2)-th (rounded up to the nearest integer) lexicographically smallest sequence是{k/2,k/2,k/2,...}的前[n/2](取下整)个序列,(即{k/2,k/2,k/2,...}再向前挪[n/2]就是答案)；

AC代码：

#include<cstdio>
#include<algorithm>
using namespace std;

int ans[300010];

int main()
{
   int k,n;scanf("%d%d",&k,&n);
   if(k%2==0){
      printf("%d",k/2);
      for(int i=2;i<=n;i++){
        printf(" %d",k);
      }
      printf("\n");
   }
   else{
      int t;
      if(n%2==1) t=(n-1)/2;
      else t=(n-1)/2+1;
      for(int i=1;i<=n;i++) ans[i]=k/2+1;
      int len=n;
      while(t--){
        if(ans[len]==1) len--;
        else{
            ans[len]--;
            for(int i=len+1;i<=n;i++) ans[i]=k;
            len=n;
        }
      }
      for(int i=1;i<=len;i++) {
        if(i!=1) printf(" ");
        printf("%d",ans[i]);
      }
      printf("\n");
   }
}

[思维]Finite Encyclopedia of Integer Sequences

标签：time 图片分享图片 number nbsp data seq list 技术分享

原文地址：https://www.cnblogs.com/lllxq/p/9416349.html