机器学习实战第五章Logistic回归

标签：推导   tran   blank   迭代   表示   bubuko   class   技术分享   类别   

def gradAscent(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)             #convert to NumPy matrix
    labelMat = mat(classLabels).transpose() #convert to NumPy matrix
    m,n = shape(dataMatrix)
    alpha = 0.001
    maxCycles = 500
    weights = ones((n,1))
    for k in range(maxCycles):              #heavy on matrix operations
        h = sigmoid(dataMatrix*weights)     #matrix mult
        error = (labelMat - h)              #vector subtraction
        weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
    return weights

这是书中梯度上升算法的代码，但看到倒数第三行和倒数第二行的时候就懵逼了，书中说这里略去了一个简单的数据推导，嘤嘤嘤，想了一会没想出来，于是乎就百度看看大神的解释，这是找到的一篇解释的比较好的，仔细一看发现是在Ag的机器学习视频中讲过的，忘了。。。

Sigmoid函数: $g(z)=\frac{1}{1+e^{-z}}$

　　$h_{\theta }(x)=g(\theta ^{T}x)$

这里$\theta$和书中w一样，表示系数

代价函数如下，代价函数是用来计算预测值（类别）与实际值（类别）之间的误差的

　　$cost(h_{\theta} (x),y)=\left\{\begin{matrix}
　　-log(h_{\theta}(x)), y=1\\
　　-log(1-h_{\theta}(x)), y=0\end{matrix}\right.$

写在一起表示为:

　　$cost(h_{\theta} (x),y)=-ylog(h_{\theta}(x))-(1-y)log(1-h_{\theta}(x))$

 总体的代价函数为：

　　$J(\theta)=\frac{1}{m}\sum_{m}^{i=1}cost(h_{\theta} (x^{(i)}),y^{(i)})=\frac{1}{m}\sum_{m}^{i=1}-y^{(i)}log(h_{\theta}(x^{(i)}))-(1-y^{(i)})log(1-h_{\theta}(x^{(i)}))$

要使误差最小，即求$J(\theta)$最小，也可以转化成就$-J(\theta)$的最大值，可以用梯度上升算法来求最大值，

　　　　$\theta := \theta+ \alpha \frac{\partial J(\theta )}{\partial \theta_{j}}$

下面是推导过程：

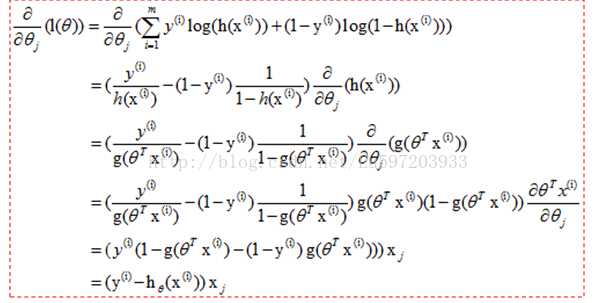
所以权重的迭代更新公式为：  

　　$\theta_{j} = \theta_{j}+ \alpha \sum_{m}^{i=1}(y_{i}-h_{\theta}(x^{(i)}))x^{(i))}$

机器学习实战第五章Logistic回归

标签：推导   tran   blank   迭代   表示   bubuko   class   技术分享   类别   

原文地址：https://www.cnblogs.com/weiququ/p/9414746.html