标签:diff 平均数 org 情况 read 可能性 ebe 间隔 一点
日常工作中对比函数间的快慢时,最直接的方法就是根据timer:tc/1结果的时间来衡量,比如想知道lists:reverse/1与直接使用自己写的尾递归函数谁更快?最直接的方法就是
-module(test).
-export([start/1]).
start(Len) ->
L = lists:seq(1, Len),
Max = 1000,
Time1 = benchmark(Max, fun() -> lists:reverse(L) end),
Time2 = benchmark(Max, fun() -> tail_reverse(L) end),
Time1/Time2.
benchmark(Max, Fun) -> benchmark(Max, Fun, 0).
benchmark(0, _Fun, Time) -> Time;
benchmark(Count, Fun, Acc) ->
{Time, _} = timer:tc(Fun),
benchmark(Count - 1, Fun, Time + Acc).
tail_reverse(L) -> tail_reverse(L, []).
tail_reverse([], Acc) -> Acc;
tail_reverse([X | Xs], Acc) -> tail_reverse(Xs, [X | Acc]).
在shell中直接运行
1> [begin test:start(Len) end||Len<-lists:seq(1,10000, 1000)].
[0.9605911330049262,0.9538599640933573,0.4008409250175193,
0.4468459717078502,0.42090136752676627,0.5073483137748491,
0.4653574844571975,0.47523496362271184,0.508740383302226,
0.5094403169886083]可以看出,lists:reverse/1比尾递归快,且列表长度越大时,lists:reverse/1越优。
但是以上的结论建立在所有的测试条件完全一致的情况下。但达到完全一致是完全不可能的,因为在Erlang VM在测试过程中也可能在做其它的事(GC,其它调度工作). 即便再优化代码,尽量保持VM不在干其它的事,但是还需要保证测试过程中操作系统条件一致,假如测试时使用的是笔记本电脑测试,你可能会在测试的过程中不经意的切换了一下web浏览器,看一下视频,邮件,或者由于电量问题系统自动切换了CPU的频次。
换句话来说,有太多扰乱性能测试结果的因素,其中有一些我们无法察觉或无法控制的,但它们可能不会发生或可能不重要,这些变数混杂在一起让本来需要精确对比的结果变得难以衡量。
所以这种求平均数的方法在需要精确对比的性能测试中并没有十足的说服力。Student‘t T-Test就是专用于解决这类问题的。
T-Test通过对比平均数(averages)和调和平均数(means),可以告诉你样本间不同的程度有多大。它可以让你知道这些差异是否是偶然发生的。举个例子:
一家制药公司可能想要测试一种新的抗癌药物,以确定它是否可以提高预期寿命。在一项实验中,总有一个对照组(给予安慰剂的组)。对照组可能显示平均预期寿命为+5年,而服用新药的组可能预期寿命为+6岁。似乎该药物可能起作用。但这可能是由于侥幸。为了测试这一点,研究人员将使用T-Test检验来确定整个人群的结果是否可重复。
T-Test看起来几乎与正态分布曲线相同,只是更短更胖。当您有小样本时,使用t分布而不是正态分布。样本量越大,t分布越接近正态分布。实际上,对于大于20的样本大小(例如:更大的自由度),分布几乎与正态分布完全相同。
如何一步一步手动计算配对T-Test。
假如有以下两个样本。
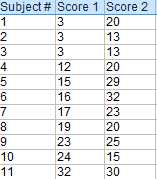
使用X-Y得到差值。
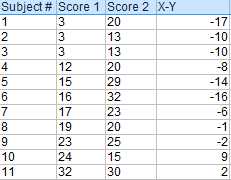
把上一步得到的所有差值都相加。
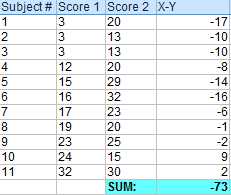
计算第一步中X-Y的平方值。
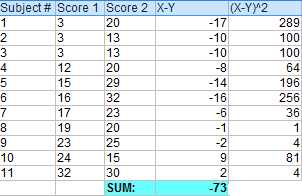
把第三步中的所有平方值相加。
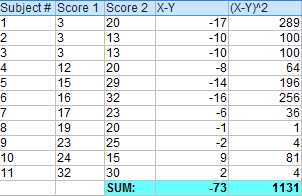
使用公式计算t-score。
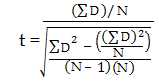
ΣD: Sum of the differences (Sum of X-Y from Step 2)
ΣD2: Sum of the squared differences (from Step 4)
(ΣD)2: Sum of the differences (from Step 2), squared.
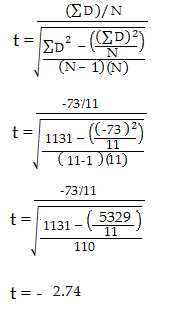
通过查t-table表得到p-value。使用第6步得到的自由度查表。我们使用95%的Confidence level, 所以对应的此样本是 df=10 alpha level = 5% 查得t-value为2.228。
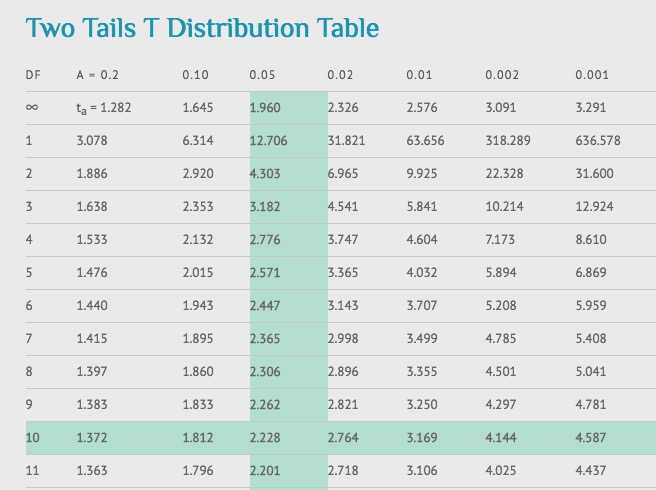
对比2.228和在第5步计算的-2.74, -2.74的绝对值大于2.228所以 p-value < 0.05。我们可以拒绝无效假设,即均值之间没有区别。
那么如何把T-Test运用到我们的性能测试中呢?
eminstat就是使用T-Test方法来测试检验样本间是否有差异的库。它使用非常简单,不过要完全看懂它的结果,必须要对T-Test有一定的了解。
下面我们还是以reverse的例子来详细介绍一下eminstat使用和结果分析。
rebar3 new lib bencherl
===> Writing bencherl/src/bencherl.erl
===> Writing bencherl/src/bencherl.app.src
===> Writing bencherl/rebar.config
===> Writing bencherl/.gitignore
===> Writing bencherl/LICENSE
===> Writing bencherl/README.md
cat rebar.config
{deps, [{eminstat, {git, "https://github.com/jlouis/eministat.git", {branch, master}}}]}.
rebar3 compilecat ebench_reverse.erl
-module(ebench_reverse).
-export([t/0, t/2]).
-define(LOOP, 1000).
t() ->
t(1000, 40).
t(Len, Count) ->
[H | T] = datasets(Len, Count),
eministat:x(95.0, H, T).
lists_r(Items) -> lists_r(Items, ?LOOP).
lists_r(_, 0) -> ok;
lists_r(Items, K) ->
lists:reverse(Items),
lists_r(Items, K-1).
tail_r(Items) -> tail_r(Items, ?LOOP).
tail_r(_, 0) -> ok;
tail_r(Items, K) ->
tail_reverse(Items),
tail_r(Items, K-1).
datasets(Len, Count) ->
Items = lists:seq(1, Len),
[
eministat:s("lists:reverse", fun() -> lists_r(Items) end, Count),
eministat:s("tail_reverse", fun() -> tail_r(Items) end, Count)
].
tail_reverse(L) -> tail_reverse(L, []).
tail_reverse([], Acc) -> Acc;
tail_reverse([X | Xs], Acc) -> tail_reverse(Xs, [X | Acc]).rebar3 shell
1>ebench_reverse:t(3000, 30).
x lists:reverse
+ tail_reverse
+--------------------------------------------------------------------------+
|xxxxxxx x ++++ +|
|xxxxx x ++++ |
|xxxx +++ |
|xxx +++ |
|xx +++ |
| x +++ |
| x + |
| x + |
| x + |
| x + |
| x + |
| x + |
| + |
| + |
| + |
||MA_| |
| |___MA____| |
+--------------------------------------------------------------------------+
Dataset: x N=30 CI=95.0000
Statistic Value [ Bias] (Bootstrapped LB‥UB)
Min: 8295.00
1st Qu. 8494.00
Median: 8700.00
3rd Qu. 9467.00
Max: 1.14400e+4
Average: 9088.53 [ -3.07012] ( 8849.00 ‥ 9447.13)
Std. Dev: 831.129 [ -28.0026] ( 608.188 ‥ 1129.95)
Outliers: 0/1 = 1 (μ=9085.46, σ=803.126)
Outlier variance: 0.484430 (moderate)
------
Dataset: + N=30 CI=95.0000
Statistic Value [ Bias] (Bootstrapped LB‥UB)
Min: 2.67010e+4
1st Qu. 2.70370e+4
Median: 2.71440e+4
3rd Qu. 2.75240e+4
Max: 3.82770e+4
Average: 2.76068e+4 [ -3.36850] ( 2.72001e+4 ‥ 2.91141e+4)
Std. Dev: 2043.00 [ -372.223] ( 307.987 ‥ 4224.71)
Outliers: 0/1 = 1 (μ=2.76034e+4, σ=1670.78)
Outlier variance: 0.384784 (moderate)
Difference at 95.0% confidence
1.85183e+4 ± 806.172
203.754% ± 8.87022%
(Student's t, pooled s = 1559.59)
------
ok我们对长度为3000的List做reverse,取样30次。得到上面的结果。
我们的数据必须是正态分布,2组样本的方差要一致。如果不一致,测试结果就无效,你必须找其它更厉害的工具(比如:R Tool)来分析。
首先收集样本
DataSet = eminstat:s(Name, Function, N) : 运行Function N次,并收集每一次的运行时间做为DataSet。然后使用:
eninistat:x(ConfidenceLevel, DataSet1, [DataSet,...])来分析样本。
ConfidenceLevel可以为[80.0,90.0,95.0,98.0,99.0,99.5] 一般使用95%就够了。用于查表得到t-value。
结果包括4个部分:
图表(histogram)
对每一组样本
要素(vitals)
孤立点分析(outlier analysis)
T-Test结果x lists:reverse
+ tail_reverse
+--------------------------------------------------------------------------+
|xxxxxxx x ++++ +|
|xxxxx x ++++ |
|xxxx +++ |
|xxx +++ |
|xx +++ |
| x +++ |
| x + |
| x + |
| x + |
| x + |
| x + |
| x + |
| + |
| + |
| + |
||MA_| |
| |___MA____| |
+--------------------------------------------------------------------------+把样本的所有的数据都使用ASCII art的点到图表上,可以看到数据总体分布。如果数据有重叠的,就使用*来代替。
M代表median中位数,
A代表Average/Mean平均数。
如果只显示一个A,就说明MA重叠了。
|____…____|代表假定为正态分布的数据集时表示1个标准偏差。越窄越稳定。
Dataset: x N=30 CI=95.0000
Statistic Value [ Bias] (Bootstrapped LB‥UB)
Min: 8295.00
1st Qu. 8494.00
Median: 8700.00
3rd Qu. 9467.00
Max: 1.14400e+4
Average: 9088.53 [ -3.07012] ( 8849.00 ‥ 9447.13)
Std. Dev: 831.129 [ -28.0026] ( 608.188 ‥ 1129.95)N 样本的个数。
CI 上面说的信任等级[80.0,90.0,95.0,98.0,99.0,99.5]
Min 最小值
Max 最大值
Median 中位数
1st Qu 1/4的中位数位置(就是min与Median之前的中位数)
3st Qu 3/4的中位数位置(就是Median与Max之前的中位数)
Average 计算数据集的平均值以及标准偏差
为了比单点估计更精确,还提供了具有下限和上限的平均值和标准差的间隔。也就是说,eministat可以从这个特定样本获得的平均值是8849 ‥ 9447,而不是告诉平均值是9088作为一个点。
置信等级为95%并不意味着真实的总体平均值的可能性为95%,没有任何程序可以做到这点,它代表:
如果你要重复这个实验数千次,并且你会设置每个样本的(不同的)置信区间,那么它有95%的概率是会包含真实的平均值。
系统使用偏差校正的加速引导方法(bias-corrected accelerated bootstrap method)来计算间隔的边界。它还计算从引导程序到样本参数的偏差。在上面的例子中,你会在Std中看到-28的偏差。这个偏差意味着一般引导程序(bootstrap)获得比样本估计值更小的标准偏差。
Outliers: 0/1 = 1 (μ=9085.46, σ=803.126)
Outlier variance: 0.484430 (moderate)emninstat使用非常简单计算孤立点的方法
IQR = Q3 - Q1所以离中位数有1.5IQR的都会被认为是孤立点。
Lower/Upper 代表着较低的异常值低于平均值的个数/较高的异常值高于平均值的个数。
Outlier variance 孤立点的方差,代表着孤立点对最终结果的影响程度,等级为
unaffected‥slight‥moderate‥severe 如果结果为severe,你就应该想办法优化一下样本,来避免这种影响。
影响孤立点的因素有很多:垃圾回收,CPU频次变化,其它系统的后台任务。
Difference at 95.0% confidence
1.85183e+4 ± 806.172
203.754% ± 8.87022%
(Student's t, pooled s = 1559.59)上面代表着:
1.85183e+4 ± 806.172: 平均值(means) ± 间隔(interval)。203.754% ± 8.87022%所以上面的结果可以确切得出: lists:reverse比尾递归快得多,且稳定。

http://www.statisticshowto.com/probability-and-statistics/t-test/
https://en.wikipedia.org/wiki/Pooled_variance
https://github.com/jlouis/eministat
标签:diff 平均数 org 情况 read 可能性 ebe 间隔 一点
原文地址:https://www.cnblogs.com/zhongwencool/p/student_t_test.html