标签:main 时域 src parse atl rsh bsp problem color

证明:
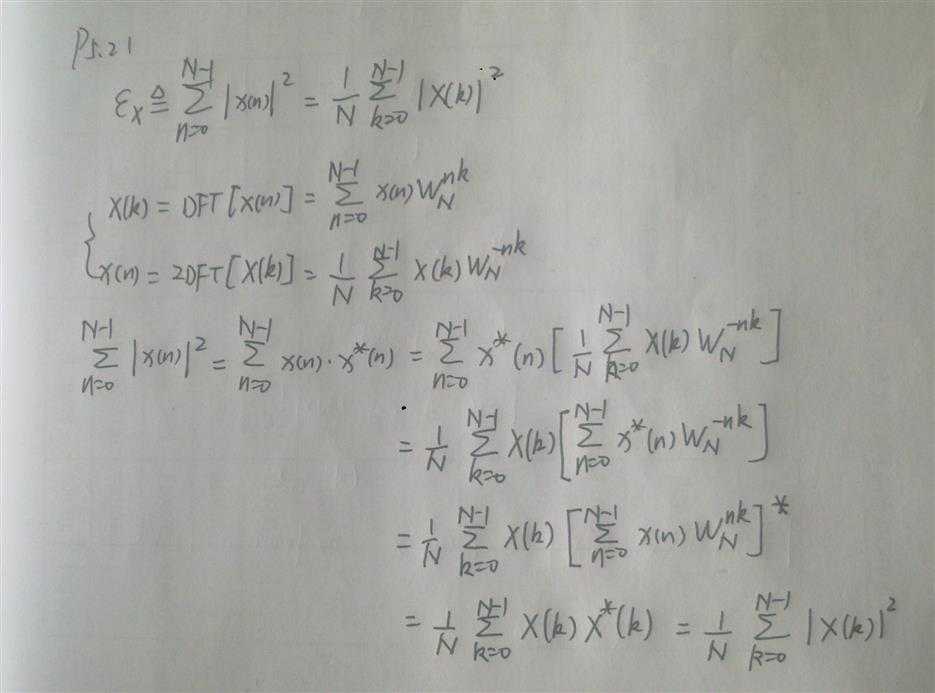
代码:
%% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
%% Output Info about this m-file
fprintf(‘\n***********************************************************\n‘);
fprintf(‘ <DSP using MATLAB> Problem 5.21 \n\n‘);
banner();
%% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
% ---------------------------------------------------------------------------------
%
% Parseval relation
% sum[abs(x(n))^2] = sum[abs(X(k))^2]/N
%
% ---------------------------------------------------------------------------------
n = [0:10];
x = [5, 4, 3, 2, 1, 0, 0, 1, 2, 3, 4]; % N=11 sequence
N = length(x);
Exn = sum(abs(x).^2)
m1 = -5; N1 = 12;
n1 = [0:N1-1];
m2 = 8; N2 = 15;
n2 = [0:N2-1];
% -----------------------------------------------------
% 1st way to get circular shift---time domain
% -----------------------------------------------------
y1_1 = cirshftt(x, m1, N1);
y2_1 = cirshftt(x, m2, N2);
% --------------------------------------------------------
% 2rd way to get circular shift --- freq domain
% --------------------------------------------------------
y1_2 = cirshftf(x, m1, N1);
y2_2 = cirshftf(x, m2, N2);
figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘P5.21.a x(n) and its cir shift‘)
set(gcf,‘Color‘,‘white‘);
subplot(3,1,1); stem(n, x);
xlabel(‘n‘); ylabel(‘x(n)‘);
title(‘x(n), N=11‘); grid on;
subplot(3,1,2); stem(n1, y1_1);
xlabel(‘n‘); ylabel(‘y(n)‘);
title(‘TIME domain circular shift x(n), m=-5, N=12‘); grid on;
subplot(3,1,3); stem(n1, y1_2);
xlabel(‘n‘); ylabel(‘y(n)‘);
title(‘FREQ domain circular shift x(n), m=-5, N=12‘); grid on;
axis([0, N1, 0, 6]);
figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘P5.21.b x(n) and its cir shift‘)
set(gcf,‘Color‘,‘white‘);
subplot(3,1,1); stem(n, x);
xlabel(‘n‘); ylabel(‘x(n)‘);
title(‘x(n), N=11‘); grid on;
subplot(3,1,2); stem(n2, y2_1);
xlabel(‘n‘); ylabel(‘y(n)‘);
title(‘TIME domain circular shift x(n), m=8, N=15‘); grid on;
subplot(3,1,3); stem(n2, y2_2);
xlabel(‘n‘); ylabel(‘y(n)‘);
title(‘FREQ domain circular shift x(n), m=8, N=15‘); grid on;
axis([0, N2-1, 0, 6]);
% ----------------------------------------------------
% DFT of sequence
% ----------------------------------------------------
Xk_DFT = dft(x, N);
k = n;
magXk_DFT = abs( [ Xk_DFT ] ); % DFT magnitude
angXk_DFT = angle( [Xk_DFT] )/pi; % DFT angle
realXk_DFT = real(Xk_DFT);
imagXk_DFT = imag(Xk_DFT);
EXk = sum(magXk_DFT .^ 2)/N
Y11k_DFT = dft(y1_1, N1);
k1 = n1;
magY11k_DFT = abs( [ Y11k_DFT ] ); % DFT magnitude
angY11k_DFT = angle( [Y11k_DFT] )/pi; % DFT angle
realY11k_DFT = real(Y11k_DFT);
imagY11k_DFT = imag(Y11k_DFT);
EY11k = sum(magY11k_DFT.^2)/N1
Y21k_DFT = dft(y2_1, N2);
k2 = n2;
magY21k_DFT = abs( [ Y21k_DFT ] ); % DFT magnitude
angY21k_DFT = angle( [Y21k_DFT] )/pi; % DFT angle
realY21k_DFT = real(Y21k_DFT);
imagY21k_DFT = imag(Y21k_DFT);
EY21k = sum(magY21k_DFT.^2)/N2
figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘P5.21 X(k), DFT of x(n)‘)
set(gcf,‘Color‘,‘white‘);
subplot(2,2,1); stem(k, magXk_DFT);
xlabel(‘k‘); ylabel(‘magnitude(k)‘);
title(‘magnitude DFT of x(n), N=11‘); grid on;
subplot(2,2,3); stem(k, angXk_DFT);
%axis([-N/2, N/2, -0.5, 50.5]);
xlabel(‘k‘); ylabel(‘angle(k)‘);
title(‘angle DFT of x(n), N=11‘); grid on;
subplot(2,2,2); stem(k, realXk_DFT);
xlabel(‘k‘); ylabel(‘real (k)‘);
title(‘real DFT of x(n), N=11‘); grid on;
subplot(2,2,4); stem(k, imagXk_DFT);
%axis([-N/2, N/2, -0.5, 50.5]);
xlabel(‘k‘); ylabel(‘imag (k)‘);
title(‘imag DFT of x(n), N=11‘); grid on;
figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘P5.21 Y11(k), DFT of x((n+5))12‘)
set(gcf,‘Color‘,‘white‘);
subplot(2,2,1); stem(k1, magY11k_DFT);
xlabel(‘k‘); ylabel(‘magnitude(k)‘);
title(‘magnitude DFT of y11(n), N=12‘); grid on;
subplot(2,2,3); stem(k1, angY11k_DFT);
%axis([-N/2, N/2, -0.5, 50.5]);
xlabel(‘k‘); ylabel(‘angle(k)‘);
title(‘angle DFT of y11(n), N=12‘); grid on;
subplot(2,2,2); stem(k1, realY11k_DFT);
xlabel(‘k‘); ylabel(‘real (k)‘);
title(‘real DFT of y11(n), N=12‘); grid on;
subplot(2,2,4); stem(k1, imagY11k_DFT);
%axis([-N/2, N/2, -0.5, 50.5]);
xlabel(‘k‘); ylabel(‘imag (k)‘);
title(‘imag DFT of y11(n), N=12‘); grid on;
figure(‘NumberTitle‘, ‘off‘, ‘Name‘, ‘P5.21 Y21(k), DFT of x((n-8))15‘)
set(gcf,‘Color‘,‘white‘);
subplot(2,2,1); stem(k2, magY21k_DFT);
xlabel(‘k‘); ylabel(‘magnitude(k)‘);
title(‘magnitude DFT of y21(n), N=15‘); grid on;
subplot(2,2,3); stem(k2, angY21k_DFT);
%axis([-N/2, N/2, -0.5, 50.5]);
xlabel(‘k‘); ylabel(‘angle(k)‘);
title(‘angle DFT of y21(n), N=15‘); grid on;
subplot(2,2,2); stem(k2, realY21k_DFT);
xlabel(‘k‘); ylabel(‘real (k)‘);
title(‘real DFT of y21(n), N=15‘); grid on;
subplot(2,2,4); stem(k2, imagY21k_DFT);
%axis([-N/2, N/2, -0.5, 50.5]);
xlabel(‘k‘); ylabel(‘imag (k)‘);
title(‘imag DFT of y21(n), N=15‘); grid on;
运行结果:
序列的圆周移位
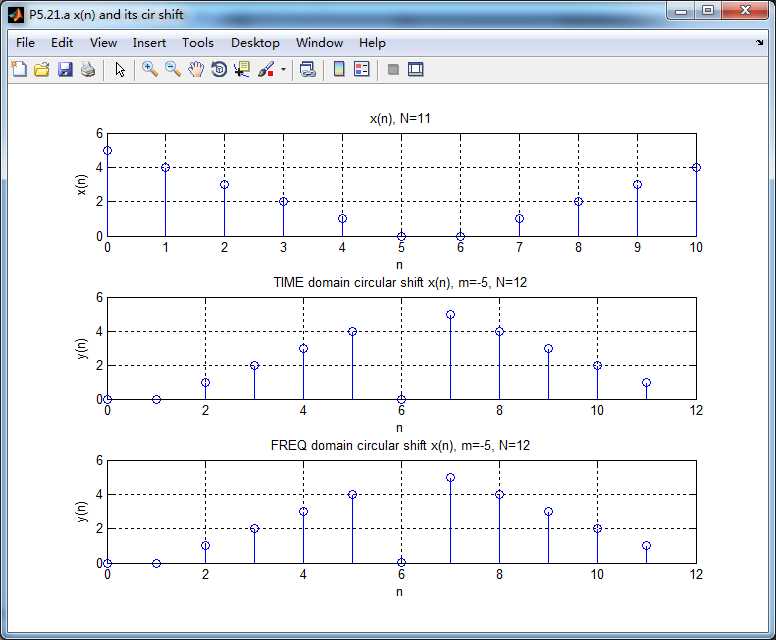
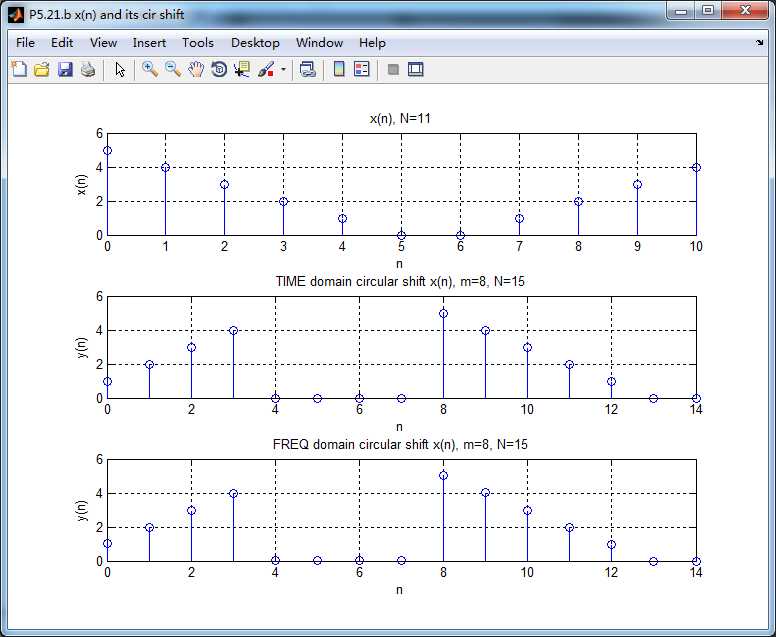
原始序列x(n)的DFT
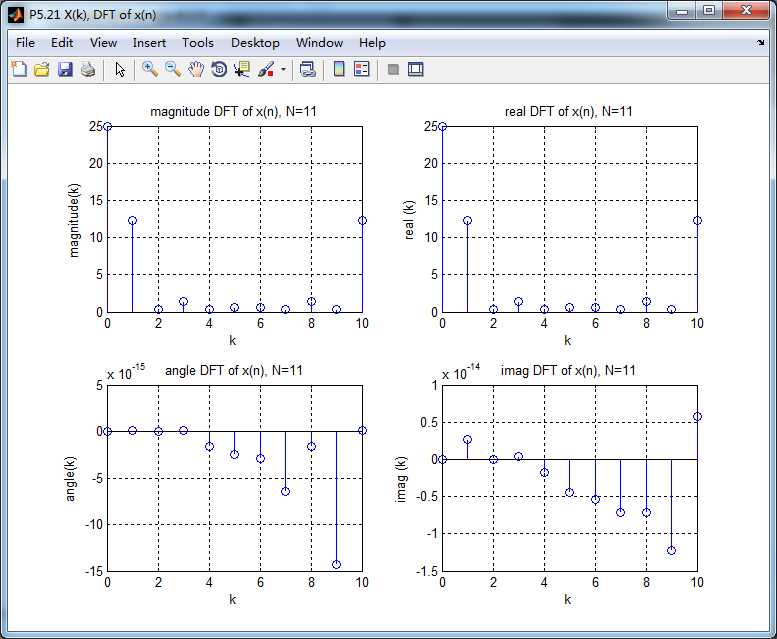
圆周移位序列1的DFT
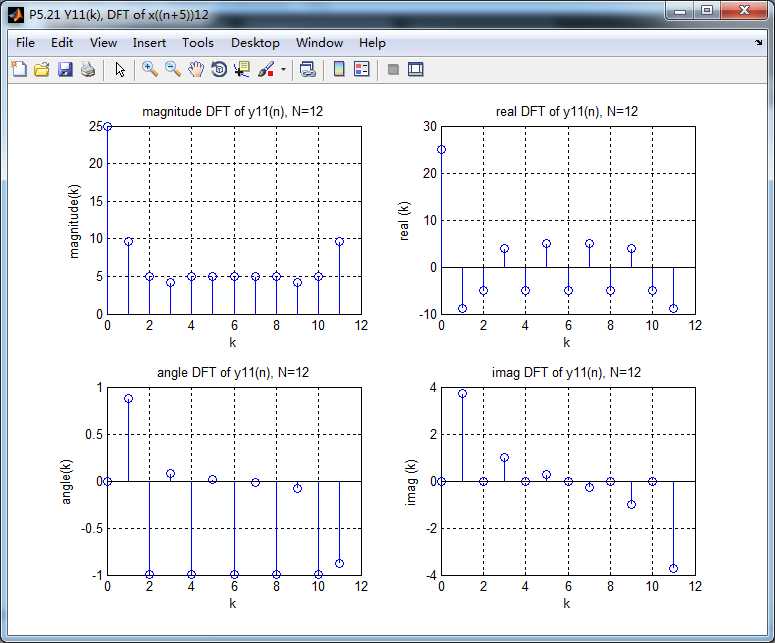
圆周移位序列2的DFT
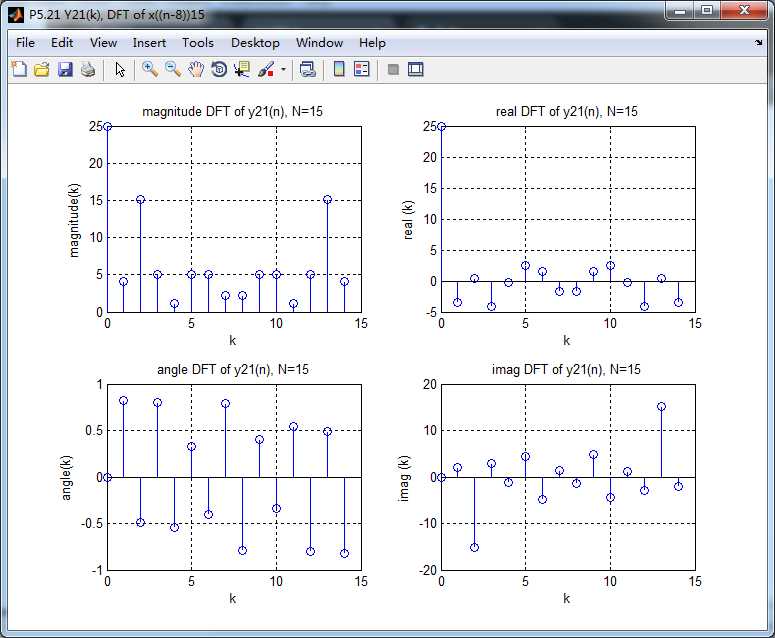
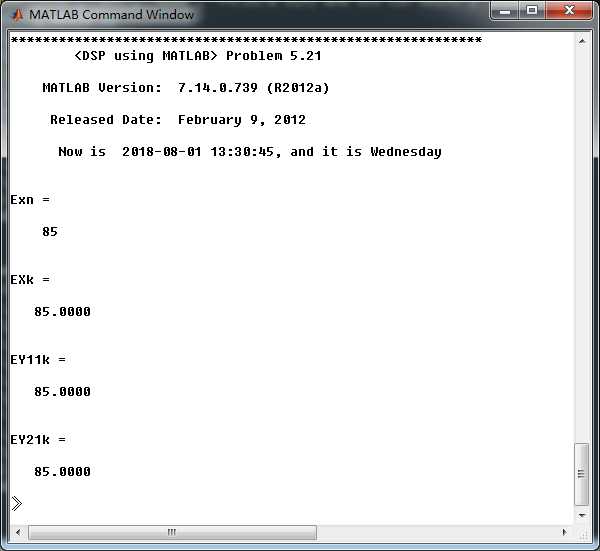
上图可知,时域的能量和频域的能量相等。
《DSP using MATLAB》Problem 5.21
标签:main 时域 src parse atl rsh bsp problem color
原文地址:https://www.cnblogs.com/ky027wh-sx/p/9429760.html