标签：car   大小   tput   ott   repeat   rmi   ace   start   height   

Trucking

Time Limit: 20000/10000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 11419    Accepted Submission(s): 1101

题意：有c个城市，r条连接两个不同城市的道路，每条道路都有长度和限制货物的最大高度，货物的高度越高

则能运输的货物越多，所以商人老板想从城市a到城市能运输货物的高度最大可以是多少，当高度最大时，要走的路程总长最短是多少。

输入给出 c 和 r 的大小，接下来有 r 行代表着每条道路的信息，每一行给出相连的城市a，b，道路限制的最大高度（-1代表高度不受限制），道路的长度，道路是双向的。

最后一行给出出发城市，目的城市，货物能到达的初始最大高度。

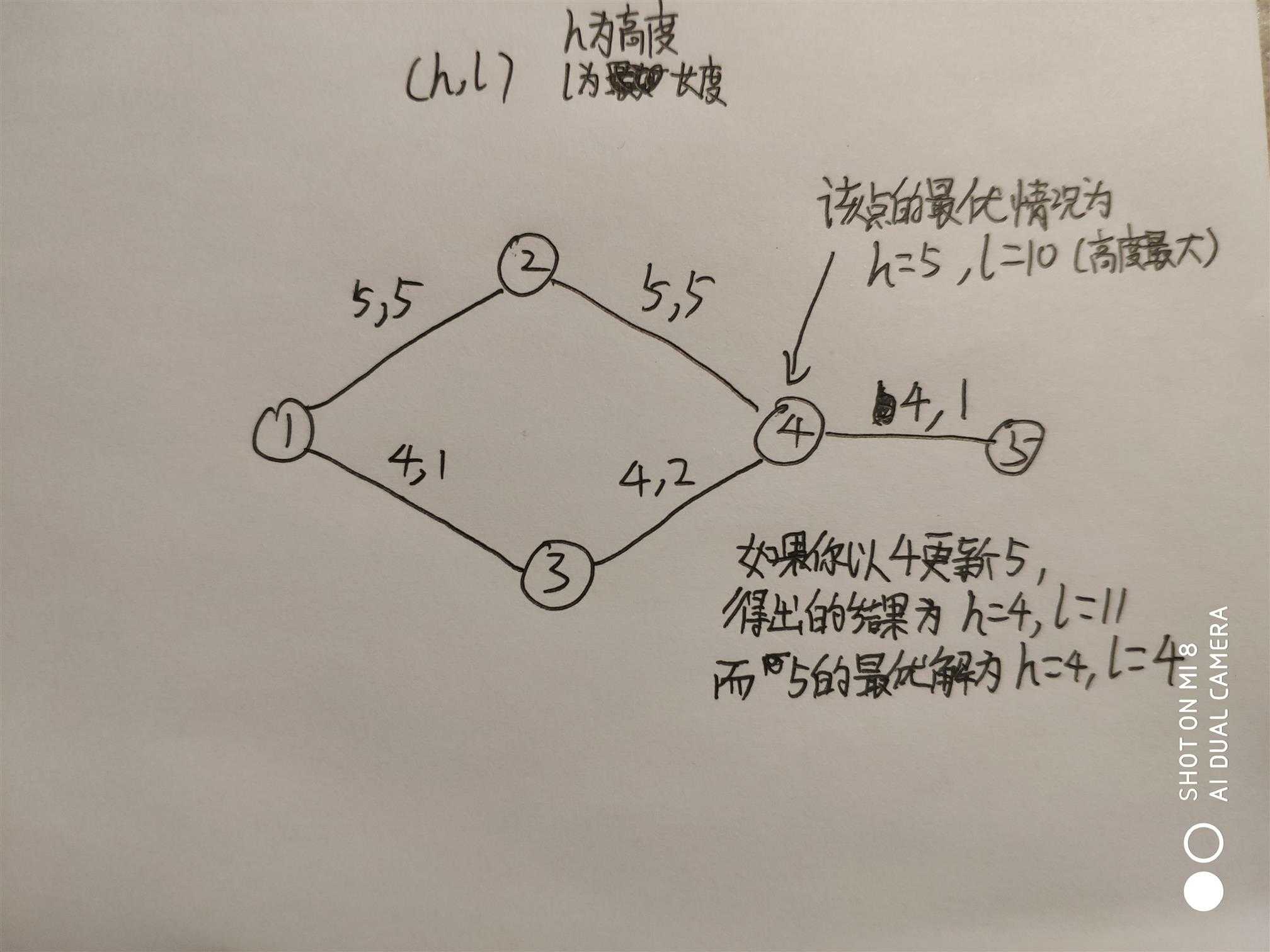
思路：简单的dijkstra的运用，先用此算法求出能运输的最大高度，再以求出的最大高度为限制求出要走的最短路程。但是要注意不能同时求最大高度和最段路径，

因为当你求出一个点的最大高度和最短路程时，你不能以该点的最段路程来退出它后面点的最短路程，因为加设你当前求出的最大高度为h，最短路径为l，那么如果它连接下一个点的道路的限制小于你当前的最大高度时，你就不能保证下一个点的最短路径是最短的

看下图就知道了

代码

#include<cstdio>
#include<algorithm>
#include<cstring>
#define INF 0x3fffffff
using namespace std;
struct st{
	int h,l;
}mp[1010][1010];
st dis[1010];
int vt[1010];
int n,m,nb;
int a2,b2,h2;
int dij(){
	int i,j,k;
	int mx,mn;
	int h;
	int c,d,a1;
	for(i=1;i<=n;i++){//初始化 
		dis[i].l=INF;
		dis[i].h=-1;
	}
	dis[a2].l=0;//初始化开始点 
	dis[a2].h=h2;
	k=a2;
	while(k!=-1){//求高度 
		vt[k]=1;
		mx=0;//高度 
		for(i=1;i<=n;i++){
			if(!vt[i]&&mp[k][i].l!=-1){ 
				if(dis[i].h<(min(mp[k][i].h,dis[k].h))){//更新每个点的最大高度 
					dis[i].h=min(mp[k][i].h,dis[k].h);
	
				}
			}	
		}
		k=-1;
		for(i=1;i<=n;i++){		
		if(!vt[i]){//找出当前高度最大的点 重复操作 
			if(dis[i].h>mx){
					mx=dis[i].h;
					k=i;
				}
			}
		}
		
	}
	h=dis[b2].h;//最大高度 
	k=a2;
	//printf("ww%d\n",h);
	memset(vt,0,sizeof(vt));
	while(k!=-1){//求最短路径 
		vt[k]=1;
		mn=INF;//长度 
		for(i=1;i<=n;i++){	
			if(!vt[i]&&mp[k][i].l!=-1&&mp[k][i].h>=h){//限制条件 
				dis[i].l=min(dis[i].l,mp[k][i].l+dis[k].l);//更新路径长度 
			}	
		}
		k=-1;
		for(i=1;i<=n;i++){//找出当前路径最小的点		
			if(!vt[i]){
				if(mn>dis[i].l){
					mn=dis[i].l;
					k=i;
				}	
			}	
		}
	}
	
	if(nb>1)
	printf("\n");
	printf("Case %d:\n",nb);
	if(dis[b2].l==INF)//如果不能走到目的城市 
	printf("cannot reach destination\n");
	else
	printf("maximum height = %d\nlength of shortest route = %d\n",dis[b2].h,dis[b2].l);
	return 0;
}
int main(){	
	int i,j,l;
	int lg=0;
	nb=0;
	while(scanf("%d%d",&n,&m)&&n){		
		memset(mp,-1,sizeof(mp));//初始化 
		memset(vt,0,sizeof(vt));
		for(i=0;i<m;i++){
			scanf("%d%d%d%d",&a2,&b2,&h2,&l);//输入这条道路相连的两个城市，道路的限制高度，道路的长度 
			if(h2==-1)
			h2=INF;
			mp[a2][b2].h=h2;
			mp[a2][b2].l=l;
			mp[b2][a2]=mp[a2][b2];
		}
		scanf("%d%d%d",&a2,&b2,&h2);//输入出发城市，目的城市，限制的最大高度 
		nb++;	
		dij();
	}
	return  0;
}

A certain local trucking company would like to transport some goods on a cargo truck from one place to another. It is desirable to transport as much goods as possible each trip. Unfortunately, one cannot always use the roads in the shortest route: some roads may have obstacles (e.g. bridge overpass, tunnels) which limit heights of the goods transported. Therefore, the company would like to transport as much as possible each trip, and then choose the shortest route that can be used to transport that amount. For the given cargo truck, maximizing the height of the goods transported is equivalent to maximizing the amount of goods transported. For safety reasons, there is a certain height limit for the cargo truck which cannot be exceeded. Input The input consists of a number of cases. Each case starts with two integers, separated by a space, on a line. These two integers are the number of cities (C) and the number of roads (R). There are at most 1000 cities, numbered from 1. This is followed by R lines each containing the city numbers of the cities connected by that road, the maximum height allowed on that road, and the length of that road. The maximum height for each road is a positive integer, except that a height of ‘-1’ indicates that there is no height limit on that road. The length of each road is a positive integer at most 1000. Every road can be travelled in both directions, and there is at most one road connecting each distinct pair of cities. Finally, the last line of each case consists of the start and end city numbers, as well as the height limit (a positive integer) of the cargo truck. The input terminates when C = R = 0. Output For each case, print the case number followed by the maximum height of the cargo truck allowed and the length of the shortest route. Use the format as shown in the sample output. If it is not possible to reach the end city from the start city, print ‘cannot reach destination’ after the case number. Print a blank line between the output of the cases. Sample Input 5 6 1 2 7 5 1 3 4 2 2 4 -1 10 2 5 2 4 3 4 10 1 4 5 8 5 1 5 10 5 6 1 2 7 5 1 3 4 2 2 4 -1 10 2 5 2 4 3 4 10 1 4 5 8 5 1 5 4 3 1 1 2 -1 100 1 3 10 0 0 Sample Output Case 1: maximum height = 7 length of shortest route = 20 Case 2: maximum height = 4 length of shortest route = 8 Case 3: cannot reach destination

UVALive - 4223，hdu2962(简单dijkstra)

标签：car   大小   tput   ott   repeat   rmi   ace   start   height   

原文地址：https://www.cnblogs.com/cglongge/p/9433014.html