P3373 【模板】线段树 2

时间：2018-08-07 15:14:39 阅读：168 评论：0 收藏：0 [点我收藏+]

标签：oid char highlight radius 结果 \n printf 取模运算数列

题目描述

如题，已知一个数列，你需要进行下面三种操作：

1.将某区间每一个数乘上x

2.将某区间每一个数加上x

3.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1：格式：1 x y k 含义：将区间[x,y]内每个数乘上k

操作2：格式：2 x y k 含义：将区间[x,y]内每个数加上k

操作3：格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果

输出格式：

输出包含若干行整数，即为所有操作3的结果。

输入输出样例

输入样例#1：复制

输出样例#1：复制

17
2

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^）

样例说明：

故输出应为17、2（40 mod 38=2）

题解：

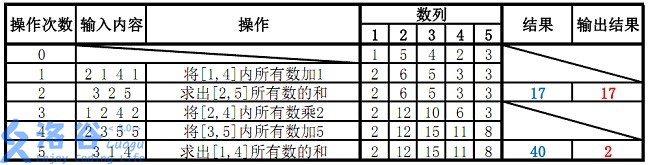
这个题真是毒瘤，疯狂卡你的时间，int,取余运算不可太多，否者时间回很多，甚至会超时，如果一开始你有30分，请看是否使用 long long，还有就是取模运算是否足够，还有就是乘法的lazyc标记在不等于-1是进行运算可能有负数。

#include <bits/stdc++.h>
using namespace std;
#define LL long long
const LL MAXN=1e6+10;
LL a[MAXN],mod;
struct node{
    LL l,r;
    long long sum;
    long long lazy;
    long long lazyc;
}Tree[MAXN<<2];
inline LL ls(LL p){ return p<<1;}//左儿子
inline LL rs(LL p){ return p<<1|1;}
void PushUP(LL p)//向上更新
{
    Tree[p].sum=(Tree[ls(p)].sum+Tree[rs(p)].sum)%mod;
    Tree[p].sum%=mod;
}
void build(LL p,LL l,LL r)
{
    Tree[p].lazy=0;
    Tree[p].lazyc=1;
    Tree[p].l=l;Tree[p].r=r;
    if(l==r) {Tree[p].sum=a[l];return;}
    LL mid=(l+r)>>1;
    build(ls(p),l,mid);
    build(rs(p),mid+1,r);
    PushUP(p);
}
void PushDown(LL p,LL l,LL r)//lazy节点下移
{
    if(Tree[p].lazy)
    {
        LL len=(r-l+1);
        Tree[ls(p)].lazy=(Tree[ls(p)].lazy%mod+Tree[p].lazy%mod)%mod;
        Tree[rs(p)].lazy=(Tree[rs(p)].lazy%mod+Tree[p].lazy%mod)%mod;

        Tree[ls(p)].sum=(Tree[ls(p)].sum%mod+Tree[p].lazy%mod*(len-(len>>1)))%mod;

        Tree[rs(p)].sum=(Tree[rs(p)].sum%mod+Tree[p].lazy%mod*(len>>1))%mod;

        Tree[p].lazy=0;//下移后，原节点取消标记
    }
}
void PushDownc(LL p,LL l,LL r)
{
    if(Tree[p].lazyc!=1)//数据中有可能有负数，
    {
        Tree[ls(p)].lazyc=(Tree[ls(p)].lazyc%mod*Tree[p].lazyc%mod)%mod;
        Tree[rs(p)].lazyc=(Tree[rs(p)].lazyc%mod*Tree[p].lazyc%mod)%mod;
        Tree[ls(p)].lazy=(Tree[ls(p)].lazy%mod*Tree[p].lazyc%mod)%mod;
        Tree[rs(p)].lazy=(Tree[rs(p)].lazy%mod*Tree[p].lazyc%mod)%mod;
        Tree[ls(p)].sum=(Tree[ls(p)].sum%mod*Tree[p].lazyc%mod)%mod;
        Tree[rs(p)].sum=(Tree[rs(p)].sum%mod*Tree[p].lazyc%mod)%mod;
        Tree[p].lazyc=1;
    }
    PushDown(p,l,r);
}
void UpDate(LL L,LL R,LL c,LL l,LL r,LL p)//更新操作
{
    if(l>=L&&r<=R)//这个区间完全在更新区间的内部
    {
        Tree[p].lazy=(Tree[p].lazy%mod+c)%mod;
        Tree[p].sum=(Tree[p].sum%mod+c*(r-l+1))%mod;
        return;
    }
    PushDownc(p,l,r);//加法的更新操作也应当使得乘法的lazyc标记向下移动
    LL mid=(l+r)>>1;
    if(mid>=L) UpDate(L,R,c,l,mid,ls(p));
    if(mid<R) UpDate(L,R,c,mid+1,r,rs(p));
    PushUP(p);
}
void Updatec(LL L,LL R,LL c,LL l,LL r,LL p)
{
    if(l>=L&&r<=R)//这个区间完全在更新区间的内部
    {
        Tree[p].lazyc=(Tree[p].lazyc%mod*c)%mod;
        Tree[p].lazy=(Tree[p].lazy%mod*c)%mod;
        Tree[p].sum=(Tree[p].sum%mod*c)%mod;

        return;
    }
    PushDownc(p,l,r);
    LL mid=(l+r)>>1;
    if(mid>=L) Updatec(L,R,c,l,mid,ls(p));
    if(mid<R) Updatec(L,R,c,mid+1,r,rs(p));
    PushUP(p);
}
LL query(LL L,LL R,LL l,LL r,LL p)
{
    LL res=0;
    if(l>=L&&r<=R) return Tree[p].sum%mod;
    LL mid=(l+r)>>1;

    PushDownc(p,l,r);

    if(mid>=L) res+=(query(L,R,l,mid,ls(p))%mod);
    if(mid<R) res+=(query(L,R,mid+1,r,rs(p))%mod);
    return res%mod;
}
int main()
{
    LL n,m;
    scanf("%lld%lld%lld",&n,&m,&mod);
    for (LL i = 1; i <=n ; ++i) {
        scanf("%lld",&a[i]);
    }
    build(1,1,n);
    while (m--)
    {
        LL flag;
        scanf("%lld",&flag);
        if(flag==1)
        {
            LL x,y,z;
            scanf("%lld%lld%lld",&x,&y,&z);
            Updatec(x,y,z%mod,1,n,1);
        }
        else if(flag==2)
        {
            LL x,y,z;
            scanf("%lld%lld%lld",&x,&y,&z);
            UpDate(x,y,z,1,n,1);
        }
        else if(flag==3)
        {
            LL x,y;
            scanf("%lld%lld",&x,&y);
            printf("%lld\n",query(x,y,1,n,1)%mod);
        }
    }
    return 0;
}

P2023 [AHOI2009]维护序列

题解：

其实是一样的题，但是直接上面那个代码有两个点过不去，因此加了一个输入挂，然后就没什么问题了。

#include <bits/stdc++.h>
using namespace std;
#define LL long long
const LL MAXN=1e6+10;
LL a[MAXN],mod;
struct node{
    LL l,r;
    long long sum;
    long long lazy;
    long long lazyc;
}Tree[MAXN<<2];
inline LL ls(LL p){ return p<<1;}//左儿子
inline LL rs(LL p){ return p<<1|1;}
void PushUP(LL p)//向上更新
{
    Tree[p].sum=(Tree[ls(p)].sum+Tree[rs(p)].sum)%mod;
    Tree[p].sum%=mod;
}
void build(LL p,LL l,LL r)
{
    Tree[p].lazy=0;
    Tree[p].lazyc=1;
    Tree[p].l=l;Tree[p].r=r;
    if(l==r) {Tree[p].sum=a[l];return;}
    LL mid=(l+r)>>1;
    build(ls(p),l,mid);
    build(rs(p),mid+1,r);
    PushUP(p);
}
void PushDown(LL p,LL l,LL r)//lazy节点下移
{
    if(Tree[p].lazy)
    {
        LL len=(r-l+1);
        Tree[ls(p)].lazy=(Tree[ls(p)].lazy%mod+Tree[p].lazy%mod)%mod;
        Tree[rs(p)].lazy=(Tree[rs(p)].lazy%mod+Tree[p].lazy%mod)%mod;

        Tree[ls(p)].sum=(Tree[ls(p)].sum%mod+Tree[p].lazy%mod*(len-(len>>1)))%mod;

        Tree[rs(p)].sum=(Tree[rs(p)].sum%mod+Tree[p].lazy%mod*(len>>1))%mod;

        Tree[p].lazy=0;//下移后，原节点取消标记
    }
}
void PushDownc(LL p,LL l,LL r)
{
    if(Tree[p].lazyc!=1)//数据中有可能有负数，
    {
        Tree[ls(p)].lazyc=(Tree[ls(p)].lazyc%mod*Tree[p].lazyc%mod)%mod;
        Tree[rs(p)].lazyc=(Tree[rs(p)].lazyc%mod*Tree[p].lazyc%mod)%mod;
        Tree[ls(p)].lazy=(Tree[ls(p)].lazy%mod*Tree[p].lazyc%mod)%mod;
        Tree[rs(p)].lazy=(Tree[rs(p)].lazy%mod*Tree[p].lazyc%mod)%mod;
        Tree[ls(p)].sum=(Tree[ls(p)].sum%mod*Tree[p].lazyc%mod)%mod;
        Tree[rs(p)].sum=(Tree[rs(p)].sum%mod*Tree[p].lazyc%mod)%mod;
        Tree[p].lazyc=1;
    }
    PushDown(p,l,r);
}
void UpDate(LL L,LL R,LL c,LL l,LL r,LL p)//更新操作
{
    if(l>=L&&r<=R)//这个区间完全在更新区间的内部
    {
        Tree[p].lazy=(Tree[p].lazy%mod+c)%mod;
        Tree[p].sum=(Tree[p].sum%mod+c*(r-l+1))%mod;
        return;
    }
    PushDownc(p,l,r);//加法的更新操作也应当使得乘法的lazyc标记向下移动
    LL mid=(l+r)>>1;
    if(mid>=L) UpDate(L,R,c,l,mid,ls(p));
    if(mid<R) UpDate(L,R,c,mid+1,r,rs(p));
    PushUP(p);
}
void Updatec(LL L,LL R,LL c,LL l,LL r,LL p)
{
    if(l>=L&&r<=R)//这个区间完全在更新区间的内部
    {
        Tree[p].lazyc=(Tree[p].lazyc%mod*c)%mod;
        Tree[p].lazy=(Tree[p].lazy%mod*c)%mod;
        Tree[p].sum=(Tree[p].sum%mod*c)%mod;

        return;
    }
    PushDownc(p,l,r);
    LL mid=(l+r)>>1;
    if(mid>=L) Updatec(L,R,c,l,mid,ls(p));
    if(mid<R) Updatec(L,R,c,mid+1,r,rs(p));
    PushUP(p);
}
LL query(LL L,LL R,LL l,LL r,LL p)
{
    LL res=0;
    if(l>=L&&r<=R) return Tree[p].sum%mod;
    LL mid=(l+r)>>1;

    PushDownc(p,l,r);

    if(mid>=L) res+=(query(L,R,l,mid,ls(p))%mod);
    if(mid<R) res+=(query(L,R,mid+1,r,rs(p))%mod);
    return res%mod;
}
long long read()
{
    char ch=‘ ‘;
    LL ans=0;
    while(ch<‘0‘ || ch>‘9‘)
        ch=getchar();
    while(ch<=‘9‘ && ch>=‘0‘)
    {
        ans=ans*10+ch-‘0‘;
        ch=getchar();
    }
    return ans;
}
int main()
{
    LL n,m;
    scanf("%lld%lld",&n,&mod);
    for (LL i = 1; i <=n ; ++i) {
//        scanf("%lld",&a[i]);
        a[i]=read();
    }
    build(1,1,n);
    scanf("%lld",&m);
    while (m--)
    {
        LL flag;
        scanf("%lld",&flag);
        if(flag==1)
        {
            LL x,y,z;
            //scanf("%lld%lld%lld",&x,&y,&z);
            x=read();y=read();z=read();
            Updatec(x,y,z%mod,1,n,1);
        }
        else if(flag==2)
        {
            LL x,y,z;
            //scanf("%lld%lld%lld",&x,&y,&z);
            x=read();y=read();z=read();
            UpDate(x,y,z,1,n,1);
        }
        else if(flag==3)
        {
            LL x,y;
            //scanf("%lld%lld",&x,&y);
            x=read();y=read();
            printf("%lld\n",query(x,y,1,n,1)%mod);
        }
    }
    return 0;
}

P3373 【模板】线段树 2

标签：oid char highlight radius 结果 \n printf 取模运算数列

原文地址：https://www.cnblogs.com/-xiangyang/p/9436539.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行