标签：参考文献   函数   科技   表示   扫描   放松   根据   生成   对比   

傅里叶叠层成像FP(Fourier Ptychographic Imaging)

　　傅里叶叠层显微术(FPM)是一种新型的计算显微成像技术，FPM与传统显微术照明方式不同，常采用可编程LED阵列进行不同角度照明，而LED灯珠发射光强与角度有关，随角度增大光强迅速减弱，不同角度照明光强不能保证一致，导致重建图像质量下降。

　　因此,在进行相位迭代反演计算过程中，需要对不同角度照明拍摄的图像进行光强校正。

　　高分辨率是光学显微技术发展至今不断追求的目标之一。

　　南京理工大学陈钱教授课题组从基本原理、实验系统与成像模式、系统与算法的改进方法等几个方面对FPM 的研究现状、应用领域和最新进展进行了综述，并讨论了现存的一些关键问题以及今后可能的研究方向。

　　文章发表在《光学学报》 第36卷第10期“成像系统”栏目上。

叠层成像技术成像机制的理论分析与实验研究

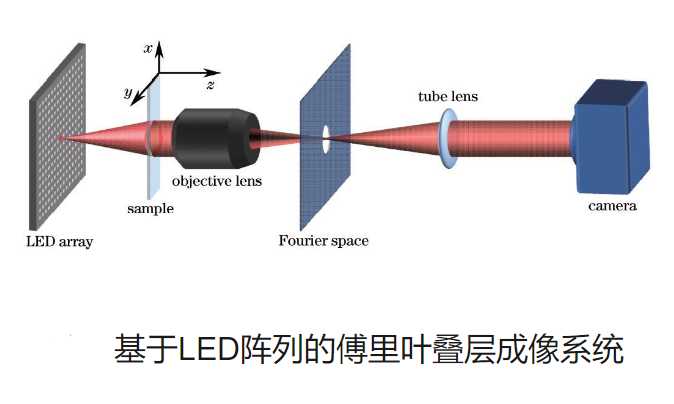
2016年西安电子科技大学的李昭慧 ：论文摘要：

　　叠层成像是近十年来新兴的一种计算成像技术。该方法通过相位恢复迭代算法,寻找样本在重叠扫描模式下,满足多幅远场衍射强度图像约束的唯一复数解。该成像技术的分辨率不受光学聚焦器件的限制,可突破系统衍射极限,获得超高分辨率成像。在一些需要从相位分量缺失的强度图像中恢复重建光波衍射信息的高分辨率和三维成像领域,叠层成像具有天然的优势和潜在的应用前景。本文围绕叠层成像的成像机理,以及它在相干衍射成像、一般光学成像及计算全息中的应用,展开了深入的研究,并对叠层成像的缺陷和不足提出了相应的解决方法。本文的主要内容如下：

1. 简要描述叠层成像的理论背景。首先,基于光波的标量衍射理论和傅里叶光学理论,对光波衍射现象,透镜的傅里叶变换作用及成像原理进行数值计算,并分析衍射受限光学系统成像分辨率存在极限的原因。其次,介绍通过干涉获取光波复振幅的全息术,并用计算生成全息图的光电再现实验验证衍射数值计算和全息成像理论的正确性。最后,介绍光相位非干涉获取的概念和相位恢复算法的数学基础——信号复原的反卷积滤波实现和迭代搜索实现理论,以及叠层成像所采用的迭代反卷积滤波器——增量维纳滤波。
2. 研究相干衍射叠层成像技术。从相干衍射成像的基本原理出发,详细分析传统相干衍射成像对样本孤立性要求和解模糊的产生机理。之后,仿真模拟相干衍射叠层成像使用光探针样本进行重叠扫描,采集记录多幅衍射强度图样,再通过迭代傅里叶变换和增量维纳滤波实现样本恢复重建的过程。定性解释叠层成像通过重叠扫描消除传统相干衍射成像的孤立样本限制和解模糊的原理,并对其中一些关键参数对重建成像的影响做出数值分析。最后,对相干衍射叠层成像检测运动样本的成像过程进行建模仿真,研究表明,由于相干衍射叠层成像图像记录时间长,采集效率低下,运动使重建像出现扭曲、模糊和噪声,像质与曝光积累时间内的样本运动幅度成反比。提出并验证了加入随机相位调制板对光探针调制,可以改善由样本运动引起的重建像降质,提高相干衍射叠层成像应对运动目标的能力,一定程度上解决其只能应对静止或低速目标的问题。
3. 研究傅里叶叠层成像技术。首先,分析傅里叶叠层成像采用倾斜入射平面波照射样本,使样本频谱与系统相干传递函数之间发生相对移动,从而实现频谱域扫描,并获得不同区域频谱对应样本强度像,再通过相位恢复算法,从这些低分辨率强度图像中重建完整样本频谱,进而获得高分辨率样本图像的原理。其次,通过对比傅里叶叠层成像和相干衍射叠层成像的异同,建立两者间的联系,证明傅里叶叠层成像同样必须遵循重叠扫描约束条件。然后借助合成孔径成像理论,定量分析傅里叶叠层成像对光学显微镜数值孔径和分辨率的提高作用。最后,为提高采集和处理的效率及系统的鲁棒性,提出相干多模态傅里叶叠层成像。利用光电调制器件调制相干光束提供相干多模态照明光照射样本,使所采集强度图像来自多个频谱片段的混叠。之后采用混叠频谱分离的相位恢复算法,从这些图像中计算得到无混叠的样本频谱和高分辨率图像。数值仿真和光电实验证明了,该方法可以显著地减少所需采集图像数量,放松对叠层成像信息复用对于共存多模态的非相干性要求。
4. 研究叠层成像在集成-全息技术中的应用。首先根据数字全息原理,计算生成三维场景的傅里叶全息图并进行数值重建与分析。其次,介绍非相干光照明下的集成成像技术,针对集成成像与全息相结合而产生的集成-全息技术,仿真实现集成成像单元图像获取、多视点投影图像生成、全息图计算生成和重建的全过程。研究表明现有集成-全息技术对光波场采样稀疏、得到全息图尺寸小、再现像分辨率低且出现视角串扰。然后,推导了多视点投影图像和傅里叶全息图之间的相关性,说明投影图像正是傅里叶全息图经过切割后的子全息图再现像的强度图像,并推导了投影角度和对应子全息图选取位置之间的关系。

　　最后,提出了通过相位恢复算法和子全息图重叠约束条件,从集成成像合成的多视点投影强度图像中重建傅里叶衍射场的计算全息方法,称之为傅里叶叠层集成全息。数值重建和光电再现实验都证明了该方法能够克服传统集成-全息的缺陷,获得高分辨率的三维全息再现像。

基于图像稀疏表示的傅里叶叠层成像算法研究

　　傅里叶叠层成像是一种整合了结构照明、叠层成像、相位恢复等理论的新型成像技术，基于该技术发明的傅里叶叠层成像显微镜利用低数值孔径、低分辨率的物镜就可以实现高分辨率和大视场成像。

　　但是,传统的傅里叶叠层成像算法采集数据时间较长，抗噪性能较差，如何在缩短数据采集时间的同时提高成像质量以及抗噪性能是当前傅里叶叠层成像算法研究的重点。本文基于压缩感知和相位恢复理论,利用稀疏先验知识对传统的傅里叶叠层成像算法进行了改进。

　　主要研究内容如下：首先,针对非抽样小波具有信息冗余性和平移不变性的特点，本文以非抽样小波作为稀疏先验，提出了基于非抽样小波正则化的傅里叶叠层成像算法并利用交替方向乘子法对该优化问题进行求解。

　　实验结果表明，与传统的傅里叶叠层成像算法相比，本文算法有效地提高了抗噪性能以及重构图像的质量。

基于稀疏表示的叠层成像算法

　　相位恢复是指利用傅立叶幅值重构原始信号。叠层成像是利用多幅相互约束的衍射图样来重建图像的复振幅信息。

　　重叠率是影响成像质量的主要因素。当重叠率相对较低时,冗余信息大量减少，传统的叠层成像相位恢复算法无法实现图像的有效重构。因此，如何引入合适的稀疏先验来提高图像重构质量是叠层成像的关键问题。

　　该文主要围绕叠层成像相位恢复算法展开研究，具体研究内容如下：

1. 1. 首先，将图像在离散余弦变换下的稀疏性引入到叠层成像相位恢复优化问题中,提出了基于离散余弦变换的叠层成像算法。通过实验对比,表明了该算法的有效性。
   2. 其次，全变差能够有效地重建图像的边缘与轮廓,提出了基于全变差的叠层成像算法。该算法将全变差正则项融合到具有幅值约束的叠层成像相位恢复问题中，实验结果表明,该算法明显优于传统叠层成像算法,并对噪声鲁棒。
   3. 最后，双树复数小波变换可以有效地保持图像的纹理信息，提出了基于双树复数小波变换的叠层成像算法。

【参考文献】

傅里叶叠层显微术的照明光强校正研究—中国光学期刊网 http://www.opticsjournal.net/Articles/Abstract?aid=OJ170308000291dJfMiP

2016/7年《光学学报》优秀综述论文_搜狐科技_搜狐网 http://www.sohu.com/a/214676149_739961

叠层成像技术成像机制的理论分析与实验研究_百度学术

基于图像稀疏表示的傅里叶叠层成像算法研究_CNKI学问 http://xuewen.cnki.net/CMFD-1017726276.nh.html 

基于稀疏表示的叠层成像算法_CNKI学问 http://xuewen.cnki.net/CMFD-1017727285.nh.html

傅里叶叠层成像FP(Fourier Ptychographic Imaging)查资料

标签：参考文献   函数   科技   表示   扫描   放松   根据   生成   对比   

原文地址：https://www.cnblogs.com/wxl845235800/p/9437777.html