逻辑回归

标签：最优   线性回归   方式   image   批量   分段   c函数   方向   逻辑   

一、逻辑回归简介

　如何凸显你是一个对逻辑回归已经非常了解的人呢。一句话概括它！逻辑回归假设数据服从伯努利分布，通过极大化似然函数的方法，运用梯度下降来求解参数，来达到将数据二分类的目的。

这里面其实包含了5个点 1：逻辑回归的假设，2：逻辑回归的损失函数，3：逻辑回归的求解方法，4：逻辑回归的目的，5:逻辑回归如何分类。这些问题是考核你对逻辑回归的基本了解。

• 逻辑回归的假设：

　　　逻辑回归的第一个基本假设是假设数据服从伯努利分布。伯努利分布有一个简单的例子是抛硬币，抛中为正面的概率是p，抛中为负面的概率是1-p，逻辑回归需要将线性模型进行一下映射，从而能用于分类。这里的映射函数或者叫分类器叫做sigmoid函数，通过sigmoid函数分类器，我们构建的逻辑回归模型是（四维为例）：

\( P(y=1|x;\theta ) = \frac{1}{1+e^{-z}} = \frac{1}{1+e^{-\theta^Tx}} \)

• 逻辑回归的损失函数：

　　　常用的损失函数有以下几种：

• • 0-1损失函数：

\(L(Y,f(X)) = \left\{\begin{matrix}1 & Y \neq f(X)\\ 0 & Y = f(X)\end{matrix}\right.\)

• • 平方损失函数：

\(L(Y,f(X)) = (Y - f(X))^2\)

• • 绝对损失函数：

\(L(Y,f(X)) = | Y - f(X))|\)

• • 对数损失函数或对数似然损失函数：

\(L(Y,P(Y|X)) = -logP(Y|X)\)

　　　对于逻辑回归模型，使用的是对数损失函数作为代价函数，则本例中，逻辑回归的损失函数为：

\(cost(y,p(y|x)) = \left\{\begin{matrix}-logp(y|x) & if(y = 1)\\ -log(1-p(y|x))& if(y = 0)\end{matrix}\right.\)

　　　将上面的两个表达式合并，则得到单个数据点上的log损失为：

\(cost(y,p(y|x)) = -ylogp(y|x) - (1-y)log(1-p(y|x))\)

　　　因为y只有两种取值情况，1或0，分别令y=1或y=0，即可得到原来的分段表达式，即两者是等价的。全体样本的损失函数则可表达为：

\(cost(y,p(y|x) = \sum_{i=1}^{m} -y_ilogp(y_i|x_i) - (1-y_i)log(1-p(y_i|x_i))\)

　　　其中\(p(y|x)\)由前面的逻辑回归模型定义，令：

\(p(y|x) = h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}}\)

　　　则最终的损失函数为：

\(cost(y,p(y|x) = \sum_{i=1}^{m} (-y_ilog\frac{1}{1+e^{-\theta^Tx}} - (1-y_i)log(1-\frac{1}{1+e^{-\theta^Tx}}))\)

•  逻辑回归的求解方法：

　　　由于该极大似然函数无法直接求解，一般通过对该函数进行梯度下降来不断逼近最优解。因为就梯度下降本身来看的话就有随机梯度下降，批梯度下降，small batch 梯度下降三种方式，面试官可能会问这三种方式的优劣以及如何选择最合适的梯度下降方式。

• • 批梯度下降会获得全局最优解，缺点是在更新每个参数的时候需要遍历所有的数据，计算量会很大，每个参数的更新都会很慢。
  • 随机梯度下降是以高方差频繁更新，优点是使得sgd会跳到新的和潜在更好的局部最优解，缺点是使得收敛到局部最优解的过程更加的复杂。
  • 小批量梯度下降结合了sgd和batch gd的优点，每次更新的时候使用n个样本。减少了参数更新的次数，可以达到更加稳定收敛结果，一般在深度学习当中我们采用这种方法。
  • 其实这里还有一个隐藏的更加深的加分项，看你了不了解诸如Adam，动量法等优化方法。因为上述方法其实还有两个致命的问题。
    • 第一个是如何对模型选择合适的学习率。自始至终保持同样的学习率其实不太合适。因为一开始参数刚刚开始学习的时候，此时的参数和最优解隔的比较远，需要保持一个较大的学习率尽快逼近最优解。但是学习到后面的时候，参数和最优解已经隔的比较近了，你还保持最初的学习率，容易越过最优点，在最优点附近来回振荡，通俗一点说，就很容易学过头了，跑偏了
    • 第二个是如何对参数选择合适的学习率。在实践中，对每个参数都保持的同样的学习率也是很不合理的。有些参数更新频繁，那么学习率可以适当小一点。有些参数更新缓慢，那么学习率就应该大一点

• 逻辑回归的目的：

　　　将数据二分类，提高准确率

• 逻辑回归如何分类：

　　　逻辑回归作为回归，如何应用到分类上去？y值确实是一个连续的变量。逻辑回归的做法是划定一个阈值，y值大于这个阈值的是一类，y值小于这个阈值的是另外一类。阈值具体如何调整根据实际情况选择。一般会选择0.5做为阈值来划分。

二、Sigmoid函数

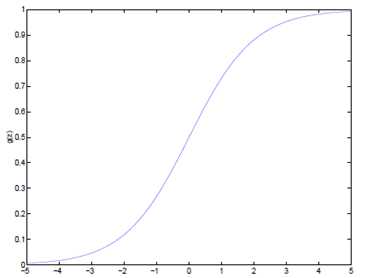
　如果我们忽略二分类问题中y的取值是一个离散的取值（0或1），我们继续使用线性回归来预测y的取值。这样做会导致y的取值并不为0或1。逻辑回归使用一个函数来归一化y值，使y的取值在区间(0,1)内，这个函数称为Logistic函数(logistic function)，也称为Sigmoid函数(sigmoid function)。函数公式如下：

\( g(z) = \frac{1}{1+e^{-z}} \)

　函数图像如下：

　该函数导数有一个特性：

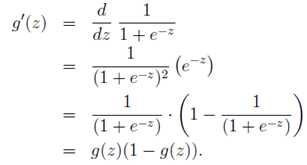
　经过Sigmoid函数转换后的y值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：

\( P(y=1|x;\theta ) = h_\theta (x) \)

\( P(y=0|x;\theta ) = 1 - h_\theta (x) \)

 　对上面的表达式合并一下就是：

\( P(y|x;\theta ) = (h_\theta (x))^y(1-h_\theta (x))^{1-y} \)

三、推导过程

　梯度上升

　　得到了逻辑回归的表达式，下一步构建似然函数，然后最大似然估计，最终推导出θ的迭代更新表达式。只不过这里用的不是梯度下降，而是梯度上升，因为这里是最大化似然函数不是最小化似然函数。我们假设训练样本相互独立，那么似然函数表达式为：

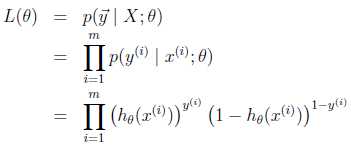
　　同样对似然函数取log，转换为：

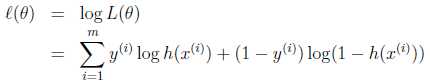
　　转换后的似然函数对θ求偏导，在这里我们以只有一个训练样本的情况为例：

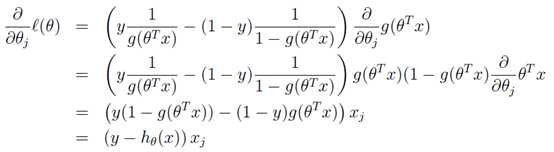
　　这样我们就得到了梯度上升每次迭代的更新方向，那么\( \theta  \)的迭代表达式为：

逻辑回归

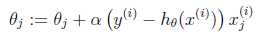
标签：最优   线性回归   方式   image   批量   分段   c函数   方向   逻辑   

原文地址：https://www.cnblogs.com/always-fight/p/9099704.html