数据归一化

标签：单位   sub   例子   图片   size   16px   font   结果   ati   

一、为何需要归一化

　不同的评价指标往往具有不同的量纲（例如：对于评价房价来说量纲指：面积、房价数、楼层等；对于预测某个人患病率来说量纲指：身高、体重等。）和量纲单位（例如：面积单位：平方米、平方厘米等；身高：米、厘米等），这样的情况会影响到数据分析的结果，为了消除指标之间量纲的影响，需要进行数据标准化处理，已解决数据指标之间的可比性。原始数据经过数据标准化处理后，各指标处于同一数量级，适合进行综合对比评价。

（1）归一化后加快了梯度下降求最优解的速度。
（2）归一化有可能提高精度（归一化是让不同维度之间的特征在数值上有一定的比较性）。

二、例子讲解

　假定为了预测房子价格，自变量为面积，房间数两个，因变量为房价，那么可以得到的公式为：\(y = \theta_1x_1 + \theta_2x_2\)，其中x₁代表房间数，x₂代表面积，首先给出两张图代表数据是否均一化的最优解寻解过程，

　未归一化：

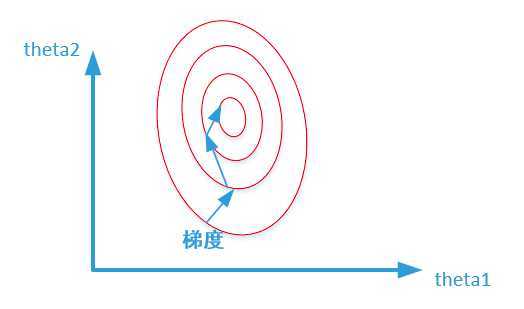
　归一化之后：

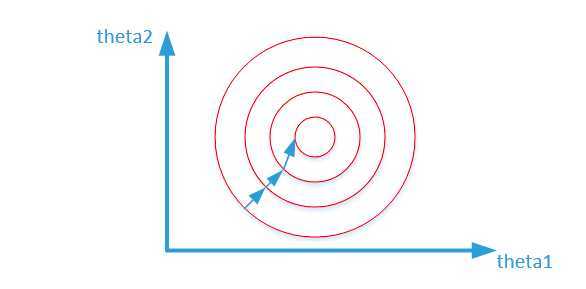
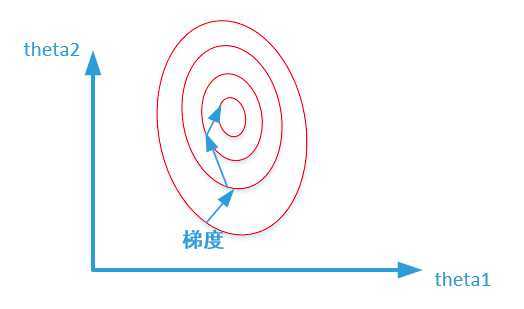
　而数据归一化后，损失函数的表达式可以表示为：\(J = (0.5\theta_1 + 0.55\theta_2 - y)^2\)，其中变量的前面系数都在【0-1】范围之间，则图像的等高线为类似的圆形形状，最优解的寻优过程如下图所示:

　

　从上面可以看出，数据归一化后，最优解的寻优过程明显会变得平缓，更容易正确的收敛到最优解。

 

三、两种常用的归一化方法：

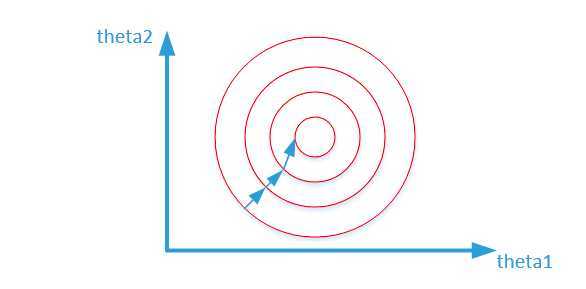
　1）min-max标准化（Min-Max Normalization）（线性函数归一化）：

• • 　定义：也称为离差标准化，是对原始数据的线性变换，使得结果映射到0-1之间。
  • 　本质：把数变为【0,1】之间的小数。
  • 　转换函数：\((X - Min)/(Max - Min)\)
  • 　如果想要将数据映射到-1,1，则将公式换成：\((X - \mu)/(Max - Min)\)

　其中：Max为样本数据的最大值，Min为样本数据的最小值，\(\mu\)表示数据的均值。缺陷：当有新数据加入时，可导致Max和Min的变化，需要重新定义。

 

　2）0均值标准化（Z-score standardlization）

• • 　定义：这种方法给与原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1.
  • 　本质：把有量纲表达式变成无量纲表达式。
  • 　转换函数：\((X - \mu)/\delta\)

　其中，\(\mu\)为所有样本数据的均值。\(\delta\)为所有样本数据的标准差。

数据归一化

标签：单位   sub   例子   图片   size   16px   font   结果   ati   

原文地址：https://www.cnblogs.com/always-fight/p/9065923.html