标签:div NPU 处理 pos pop 算法分析 ase 存在 代码
文字描述
二叉树的先根遍历
若二叉树为空,则空操纵,否则
(1) 访问根结点
(2) 先根遍历左子树
(3) 先根遍历右子树
二叉树的中根遍历
若二叉树为空,则空操纵,否则
(1) 中根遍历左子树
(2) 访问根结点
(3) 中根遍历右子树
二叉树的后根遍历
若二叉树为空,则空操纵,否则
(1) 后根遍历左子树
(2) 后根遍历右子树
(3) 访问根结点
树的先根遍历
先访问树的根结点,然后依次先根遍历树的每颗子树。
树的后根遍历
先依次后根遍历每颗子树,然后访问根结点。
森林的先根遍历
若森林非空,则:
(1) 访问森林中第一颗树的根结点
(2) 先根遍历第一个树中根结点的子树森林
(3) 先根遍历除第一颗树之后剩余的树构成的森林。
森林的中根遍历
若森林非空,则:
(1) 中根遍历森林中每一颗树的根结点的子树森林。
(2) 访问第一颗树的根结点
(3) 中根遍历除去第一颗树之后剩余的树构成的森林。
二叉树遍历算法的实现
二叉树遍历算法有三种:先根遍历、中根遍历、后根遍历; 用函数递归的方法很好实现,但是也可以不用函数递归,改用借助栈的方法, 具体描述如下:
非递归形式的二叉树的先根遍历
对于任一结点P:
(1)访问结点P,并将P入栈
(2)判断结点P的左孩子是否为空; 2.1)若为空,则取栈顶结点并进行出站并进行出栈操作,并将栈顶结点的右孩子置为当前的结点P; 2.2)若为非空, 则将P的左孩子置为当前的结点P
(3)直到P为NULL并且栈为空,则遍历结束
非递归形式的二叉树的中根遍历-方法1
对于任一结点P
(1)若其左孩子不为空,则将P入栈并将P的左孩子置为当前的P,然后对当前结点P再进行相同的处理
(2)若左孩子为空, 则取栈顶元素并进行出栈操纵, 访问该栈顶元素,然后将栈顶结点的右孩子置为当前的P
(3)直到P为NULL并且栈为空则遍历结束
非递归形式的二叉树的后根遍历
要保证根结点在左孩子和右孩子被访问之后才能访问,因此对任一结点P,先将其入栈.; 如果P不存在孩子结点, 或者其孩子结点都被访问过了,则可以直接访问它; 若非这两种情况, 则将P的右孩子和左孩子入栈; 这样就保证了每次取栈顶元素的时候,左孩子在右孩子前面被访问, 左孩子和右孩子都在根结点前面被访问
示意图
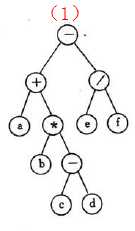
图(1)
二叉树的先根遍历 - + a * b – c d / e f
二叉树的中根遍历 a + b * c – d – e / f
二叉树的后根遍历 a b c d - * + e f / -
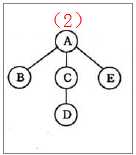
图(2)
树的先根遍历 A B C D E
树的后根遍历 B D C E A
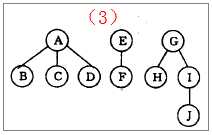
图(3)
森林的先根遍历 A B C D E F G H I J
森林的中根遍历 B C D A F E H J I G
算法分析
二叉树的遍历,无论哪种次序遍历,其时间复杂度均为n
所需辅助空间为便利过程中栈的最大深度,而最大深度为树的深度,即n
代码实现

1 #include <stdio.h> 2 #include <stdlib.h> 3 /*测试*/ 4 #define DEBUG 5 /* 6 ./a.out - + a \# \# \* b \# \# - c \# \# d \# \# / e \# \# f \# \# 7 */ 8 #define EQ(a, b) ((a)==(b)) 9 /*树中结点的最大个数*/ 10 #define MAX_TREE_SIZE 100 11 12 typedef char KeyType; 13 typedef int InfoType; 14 15 /*树中的结点类型*/ 16 typedef struct{ 17 KeyType key; 18 InfoType otherinfo; 19 }TElemType; 20 21 /* 22 * 二叉树的链式存储(二叉链表) 23 * 24 * 链表中的结点包含三个数据:数据域data,左指针域lchild,右指针域rchild 25 */ 26 typedef struct BiTNode{ 27 TElemType data; 28 struct BiTNode *lchild, *rchild; 29 }BiTNode, *BiTree; 30 31 32 /////////////////////////////////////////////////////////////////////////////////////////////////////// 33 /////////////////////////////栈的相关结点定义和与非递归遍历算法相关的栈的函数声明-start//////////////// 34 //栈的存储空间初始分配量 35 #define STACK_INIT_SIZE 100 36 //栈的存储空间分配增量 37 #define STACK_INCREMENT 10 38 //栈的结构体表示 39 typedef struct{ 40 //栈底指针 41 BiTNode *base; 42 /*栈顶指针top;插入新元素时,top增1;删除栈顶元素时,top减1; 43 *非空栈中的栈顶指针始终在栈顶元素的下一个位置上。 44 */ 45 BiTNode *top; 46 //stacksize指示栈的当前可使用的最大容量 47 int stacksize; 48 }SqStack; 49 50 /*构造一个空栈S*/ 51 int InitStack(SqStack *S); 52 53 /*若S为空栈,返回0,否则返回-1*/ 54 int StackEmpty(SqStack *S); 55 56 /*若S不为空,则用e返回S的栈顶元素,并返回0;否则返回-1*/ 57 int GetTop(SqStack *S, BiTNode *e); 58 59 /*插入元素e为新的栈顶元素*/ 60 int Push(SqStack *S, BiTNode *e); 61 62 /*若栈不为空,则删除S的栈顶元素,用e返回其值,返回0;否则返回-1*/ 63 int Pop(SqStack *S, BiTNode *e); 64 /////////////////////////////////////////////////////////////////////////////////////////////////////// 65 /////////////////////////////////////////////////////////////////////////////////////////////////////// 66 67 68 /* 69 * 按先根次序输入二叉树中结点的值,‘#‘表示空结点 70 * 构造二叉链表表示的二叉树T 71 */ 72 int I = 0; 73 BiTree CreateBiTree(TElemType input[]){ 74 TElemType data = input[I++]; 75 BiTree T = NULL; 76 if(data.key == ‘#‘){ 77 T = NULL; 78 return T; 79 }else{ 80 if(!(T=(BiTNode *)malloc(sizeof(BiTNode)))){ 81 printf("Error: overflow!\n"); 82 exit(1); 83 } 84 T->data = data; 85 T->lchild = CreateBiTree(input); 86 T->rchild = CreateBiTree(input); 87 return T; 88 } 89 } 90 91 int vist(TElemType e){ 92 printf("%c ", e.key); 93 return 0; 94 } 95 96 /*递归形式的二叉树的先根遍历算法*/ 97 int PreOrderTraverse(BiTree T, int(*fun)(TElemType e)){ 98 if(T){ 99 fun(T->data); 100 PreOrderTraverse(T->lchild, fun); 101 PreOrderTraverse(T->rchild, fun); 102 return 0; 103 }else{ 104 return 0; 105 } 106 } 107 108 /*递归形式的二叉树的中根遍历算法*/ 109 int InOrderTraverse(BiTree T, int (*fun)(TElemType e)){ 110 if(T){ 111 InOrderTraverse(T->lchild, fun); 112 fun(T->data); 113 InOrderTraverse(T->rchild, fun); 114 return 0; 115 }else{ 116 return 0; 117 } 118 } 119 120 /*递归形式的二叉树的后根遍历算法*/ 121 int PostOrderTraverse(BiTree T, int (*fun)(TElemType e)){ 122 if(T){ 123 PostOrderTraverse(T->lchild, fun); 124 PostOrderTraverse(T->rchild, fun); 125 fun(T->data); 126 return 0; 127 }else{ 128 return 0; 129 } 130 } 131 132 /* 133 *非递归形式的二叉树的先根遍历 134 * 135 *对于任一结点P 136 *(1)访问结点P,并将P入栈 137 *(2)判断结点P的左孩子是否为空 138 * 2.1 若为空,则取栈顶结点并进行出站并进行出栈操作,并将栈顶结点的右孩子置为当前的结点P 139 * 2.2 若为非空, 则将P的左孩子置为当前的结点P 140 *(3) 直到P为NULL并且栈为空,则遍历结束 141 */ 142 int PreOrderTraverse_NonRecur(BiTree T, int (*fun)(TElemType e)){ 143 SqStack S; 144 if(InitStack(&S)<0){ 145 return -1; 146 } 147 BiTNode *p = T, q; 148 while(p || StackEmpty(&S)){ 149 if(p){ 150 fun(p->data); 151 Push(&S, p); 152 p = p->lchild; 153 }else{ 154 Pop(&S, &q); 155 p = q.rchild; 156 } 157 } 158 } 159 160 /* 161 *非递归形式的二叉树的中根遍历-方法1 162 * 163 *对于任一结点P 164 *(1)若其左孩子不为空,则将P入栈并将P的左孩子置为当前的P,然后对当前结点P再进行相同的处理 165 *(2)若左孩子为空, 则取栈顶元素并进行出栈操纵, 访问该栈顶元素,然后将栈顶结点的右孩子置为当前的P 166 *(3)直到P为NULL并且栈为空则遍历结束 167 */ 168 int InOrderTraverse_NonRecur(BiTree T, int (*fun)(TElemType e)){ 169 SqStack S; 170 if(InitStack(&S)<0){ 171 return -1; 172 } 173 Push(&S, T); 174 BiTNode *p; 175 176 while(StackEmpty(&S)<0){ 177 while((!GetTop(&S, p)) && p && !Push(&S, p->lchild)); 178 Pop(&S, p); 179 fun(p->data); 180 if(StackEmpty(&S)){ 181 Pop(&S, p); 182 fun(p->data); 183 Push(&S,p->rchild); 184 } 185 } 186 return 0; 187 } 188 189 /*非递归形式的二叉树的中根遍历-方法2*/ 190 int InOrderTraverse_NonRecur2(BiTree T, int (*fun)(TElemType e)){ 191 SqStack S; 192 if(InitStack(&S)<0){ 193 return -1; 194 } 195 BiTNode *p = T, q; 196 while(p || StackEmpty(&S)){ 197 if(p){ 198 Push(&S, p); 199 p = p->lchild; 200 }else{ 201 Pop(&S, &q); 202 fun(q.data); 203 p = q.rchild; 204 } 205 } 206 } 207 208 /*比较两个结点是否相等,主要用于非递归后序遍历算法中判断两个结点是否为同一个结点*/ 209 int compare(BiTNode *node1, BiTNode *node2) 210 { 211 if(node1 == NULL|| node2 == NULL){ 212 return -1; 213 }else if((node1->data.key == node2->data.key) && (node1->data.otherinfo == node2->data.otherinfo)){ 214 return 0; 215 }else{ 216 return -1; 217 } 218 } 219 220 /* 221 *非递归形式的二叉树的后根遍历 222 * 223 *要保证根结点在左孩子和右孩子被访问之后才能访问,因此对任一结点P,先将其入栈. 224 *如果P不存在孩子结点, 或者其孩子结点都被访问过了,则可以直接访问它; 225 *若非这两种情况, 则将P的右孩子和左孩子入栈; 226 *这样就保证了每次取栈顶元素的时候,左孩子在右孩子前面被访问, 左孩子和右孩子都在根结点前面被访问 227 */ 228 int PostOrderTraverse_NonRecur(BiTree T, int (*fun)(TElemType e)){ 229 SqStack S; 230 if(InitStack(&S)<0){ 231 return -1; 232 } 233 //当前结点 234 BiTNode *curr = (BiTNode*)malloc(sizeof(BiTNode)); 235 //前一次被访问过的结点 236 BiTNode pre = {‘0‘, -1}; 237 238 Push(&S, T); 239 while(StackEmpty(&S)){ 240 GetTop(&S, curr); 241 if((curr->lchild == NULL && curr->rchild == NULL) 242 || (!compare(curr->lchild, &pre)|| !compare(curr->rchild, &pre))){ 243 //如果当前结点没有孩子结点或者该结点的孩子结点都被访问过 244 fun(curr->data); 245 pre = *curr; 246 Pop(&S, curr); 247 }else{ 248 //右孩子入栈 249 Push(&S, curr->rchild); 250 //左孩子入栈 251 Push(&S, curr->lchild); 252 } 253 } 254 255 return 0; 256 } 257 258 259 int main(int argc, char *argv[]) 260 { 261 if(argc < 2) 262 return -1; 263 264 TElemType input[MAX_TREE_SIZE]; 265 int i = 0, j = 0; 266 for(i=0; i<MAX_TREE_SIZE; i++){ 267 input[i].key = ‘#‘; 268 } 269 270 //按先根次序输入二叉树中结点的值,‘-‘表示空树 271 for(i=1; i<argc; i++){ 272 if(i>MAX_TREE_SIZE) 273 break; 274 input[i-1].key = argv[i][0]; 275 input[i-1].otherinfo = i-1; 276 } 277 #ifdef DEBUG 278 printf("按先根顺序建立二叉树(#表示空结点):\n"); 279 for(j=0; j< i-1; j++){ 280 printf("%c ", input[j].key); 281 } 282 printf("\n"); 283 #endif 284 BiTree T = CreateBiTree(input); 285 286 printf("递归形式的二叉树的先根遍历算法\n"); 287 PreOrderTraverse(T, vist); 288 289 printf("\n递归形式的二叉树的中根遍历算法\n"); 290 InOrderTraverse(T, vist); 291 292 printf("\n递归形式的二叉树的后根遍历算法\n"); 293 PostOrderTraverse(T, vist); 294 295 printf("\n非递归形式的二叉树的先根遍历\n"); 296 PreOrderTraverse_NonRecur(T,vist); 297 298 printf("\n非递归形式的二叉树的中根遍历-方法1\n"); 299 InOrderTraverse_NonRecur(T,vist); 300 301 printf("\n非递归形式的二叉树的中根遍历-方法2\n"); 302 InOrderTraverse_NonRecur2(T,vist); 303 304 printf("\n非递归形式的二叉树的后根遍历\n"); 305 PostOrderTraverse_NonRecur(T,vist); 306 printf("\n"); 307 return 0; 308 } 309 310 311 312 ///////////////////////////////////////////////////////////////////////////////////// 313 /////////////////////////////与非递归遍历算法相关的栈的函数实现-start//////////////// 314 /*构造一个空栈S*/ 315 int InitStack(SqStack *S) 316 { 317 S->base = (BiTNode *)malloc(STACK_INIT_SIZE * sizeof(BiTNode)); 318 if(!S->base){ 319 return -1; 320 } 321 S->top = S->base; 322 S->stacksize = STACK_INIT_SIZE; 323 return 0; 324 } 325 326 /*若S为空栈,返回0,否则返回-1*/ 327 int StackEmpty(SqStack *S) 328 { 329 if(S->top == S->base){ 330 return 0; 331 }else{ 332 return -1; 333 } 334 } 335 336 /*若S不为空,则用e返回S的栈顶元素,并返回0;否则返回-1*/ 337 int GetTop(SqStack *S, BiTNode *e) 338 { 339 if(S->top == S->base){ 340 return -1; 341 }else{ 342 if((S->top-1) == NULL){ 343 e = NULL; 344 }else{ 345 *e = *(S->top-1); 346 } 347 return 0; 348 } 349 } 350 351 352 /*插入元素e为新的栈顶元素*/ 353 int Push(SqStack *S, BiTNode *e) 354 { 355 //栈满,需要追加存储空间 356 if((S->top-S->base) >= S->stacksize){ 357 S->base = (BiTNode *)realloc(S->base, (S->stacksize+STACK_INCREMENT) * sizeof(BiTNode)); 358 if(!S->base){ 359 return -1; 360 } 361 S->top = S->base + S->stacksize; 362 S->stacksize += STACK_INCREMENT; 363 } 364 if(e == NULL){ 365 return -1; 366 }else{ 367 *S->top = *e; 368 } 369 S->top += 1; 370 return 0; 371 } 372 373 374 /*若栈不为空,则删除S的栈顶元素,用e返回其值,返回0;否则返回-1*/ 375 int Pop(SqStack *S, BiTNode *e) 376 { 377 if(S->top == S->base){ 378 return -1; 379 }else{ 380 S->top -= 1; 381 *e = *(S->top); 382 return 0; 383 } 384 } 385 386 ///////////////////////////////////////////////////////////////////////////////////// 387 /////////////////////////////////////////////////////////////////////////////////////
运行
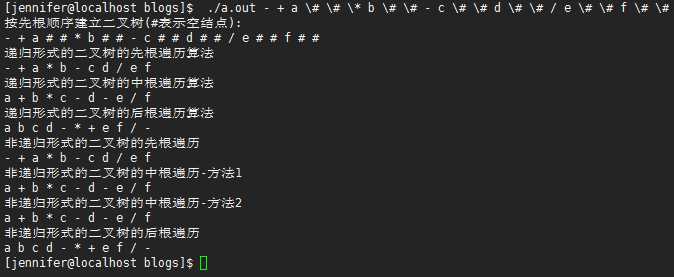
标签:div NPU 处理 pos pop 算法分析 ase 存在 代码
原文地址:https://www.cnblogs.com/aimmiao/p/9438776.html