标签:size 就是 技术 span 二叉树 bubuko bsp strong 图片
文字描述
由上篇关于树和二叉树的存储结构知,树和二叉树都可以采用二叉链表作为存储结构。也就是说,给定一颗树,可以找到惟一的一颗二叉树与之对应,从物理结构来看,它们的二叉链表是相同的,只是解释不同而已。
1 森林转换成二叉树
如果F = {T1, T2, …, Tm}是森林,需转换成一棵二叉树B={root, LB, RB}.
(1) 如果F为空,即m=0,则B为空树
(2) 如果F非空,即m !=0,则B的根root就是就是森林中第一颗树的根ROOT(T1); B的左子树LB是从ROOT(T1)的子树森林转换而成的二叉树;其中右子树RB是从森林F’ = {T2, T3, …, Tm}转换而成的二叉树。
2 二叉树转换成森林
如果B={root, LB, RB}是一颗二叉树,需转换成森林F={T1, T2, …, Tm};
(1) 如果B为空,则F为空
(2) 如果B非空,则F中第二颗树T1的根ROOT(T1)即为二叉树B的根root; T1中根结点的子树森林F1是由B的左子树LB转换而成的森林;F中除T1之外其余树组成的森林F‘ = {T2,T3,…,Tm}是由B的右子树RB转换而成的森林。
示意图

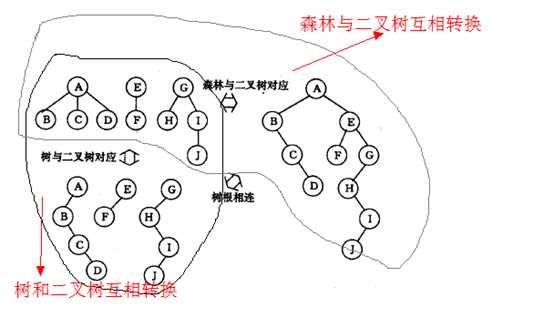
代码实现
略
标签:size 就是 技术 span 二叉树 bubuko bsp strong 图片
原文地址:https://www.cnblogs.com/aimmiao/p/9438707.html