标签:转移 数据 height puts ceo ref and 最大 处理
原题 codevs 3147 矩阵乘法2
给出两个 $ n*n $ 的矩阵,$ m $ 次询问它们的积中给定子矩阵的数值和。
第一行两个正整数 $ n,m $ 。
接下来 $ n $ 行,每行 $ n $ 个非负整数,表示第一个矩阵。
接下来 $ n $ 行,每行 $ n $ 个非负整数,表示第二个矩阵。
接下来 $ m $ 行,每行四个正整数 $ a,b,c,d $ ,表示询问第一个矩阵与第二个矩阵的积中,以第 $ a $ 行第 $ b $ 列与第 $ c $ 行第 $ d $ 列为顶点的子矩阵中的元素和。
对每次询问,输出一行一个整数,表示该次询问的答案。
$ matrix.in $
3 2
1 9 8
3 2 0
1 8 3
9 8 4
0 5 15
1 9 6
1 1 3 3
2 3 1 2 $ matrix.out $
661
388 首先,对于端点,我们确保 $ (a<c) and (b<d) $ (即把这两个坐标表示成这个子矩阵左上角和右下角的坐标)
答案为: $ \sum_{i=a}^{c} \sum_{j=b}^{d} \sum_{k=1}^{n} A[i][k]*B[k][j] $
这样就可以直接预处理前缀和
使用二维前缀和预处理 $ A[i][j] $ 表示 $ A $ 矩阵第 $ i $ 行第 $ j $ 列前 $ i $ 个数的和
使用二维前缀和预处理 $ B[i][j] $ 表示 $ B $ 矩阵第 $ i $ 行第 $ j $ 列前 $ j $ 个数的和
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,x1,x2,y1,y2;
long long a[2005][2005],b[2005][2005],ans;
int main(){
freopen("matrix.in","r",stdin);
freopen("matrix.out","w",stdout);
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j){
scanf("%d",&a[i][j]);
a[i][j]+=a[i-1][j];
}
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j){
scanf("%d",&b[i][j]);
b[i][j]+=b[i][j-1];
}
for(int i=1;i<=m;++i){
scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
ans=0;
if(x1>x2) swap(x1,x2);
if(y1>y2) swap(y1,y2);
for(int k=1;k<=n;++k)
ans+=(a[x2][k]-a[x1-1][k])*(b[k][y2]-b[k][y1-1]);
printf("%lld\n",ans);
}
return 0;
}原题:洛谷 P1632 点的移动
平面上有 $ N $ 个整数坐标点。如果将点 $ (??_0,??_0) $ 移动到 $ (??_1,??_1) $ 。则需要的代价为 $ |??_0 ???_1| + |??_0 ???_1| $ 。求使得 $ K (K=1, ......, N) $ 个点在同一位置上最少需要的代价。
第一行一个正整数 $ N $ 。
接下来N行,每行两个正整数 $ ??_i,??_I $ ,为第 $ i $ 个点的坐标。
-【输出格式】
输出共 $ N $ 行,第 $ i $ 行为使得有 $ i $ 个点在同一位置的最少代价。
-【样例】
$ tower.in $
4
15 14
15 16
14 15
16 15 $ tower.out $
0
2
3
4 -【数据范围】
$ 30 % $ 的数据: $ 0 ≤ ??_?? ≤ ??_?? ≤ 500 $ 。
$ 100 % $ 的数据:$ N ≤ 50, 0 ≤ ??_?? ≤ ??_?? ≤ 10^6 $ 。
对于枚举的点 $ (i,j) $ 来说,$ dis[p] $ 代表了 $ p $ 点移动到枚举点的代价。
可以证明枚举点的坐标一定与所有的点坐标有关。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int n,x[55],y[55],dis[55],ans[55];
int main(){
freopen("tower.in","r",stdin);
freopen("tower.out","w",stdout);
scanf("%d",&n);
memset(ans,0x3f,sizeof(int)*(n+1));
for(int i=1;i<=n;++i) scanf("%d %d",&x[i],&y[i]);
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j){
for(int p=1;p<=n;++p)
dis[p]=abs(x[p]-x[i])+abs(y[p]-y[j]);
sort(dis+1,dis+1+n);
int sum=0;
for(int i=1;i<=n;++i){
sum+=dis[i];
if(sum<ans[i]) ans[i]=sum;
}
}
for(int i=1;i<=n;++i) printf("%d\n",ans[i]);
return 0;
}原题:洛谷 P1623 [CEOI2007]树的匹配Treasury
给一棵树,你可以匹配有边相连的两个点,问你这棵树的最大匹配是多少,
并且计算出有多少种最大匹配。
第一行一个数 $ N $ ,表示有多少个节点。
接下来 $ N $ 行,每行第一个数,表示要描述的那个结点。然后一个数 $ m $ ,表示这个结点有 $ m $ 个儿子,接下来 $ m $ 个数,表示他的 $ m $ 个儿子的编号。
-【输出格式】
输出两行,第一行输出最大匹配数,第二行输出最大匹配方案数。
-【样例】
$ tree.in $
7
1 3 2 4 7
2 1 3
4 1 6
3 0
7 1 5
5 0
6 0 $ tree.out $
3
4 -【数据范围】
$ 60 % $ 的数据:答案不超过 $ 10^{18} $ 。
$ 100 % $ 的数据:$ N ≤ 1000 $ 。
树形 $ DP $
设 $ f[u][0] $ 表示在以 $ u $ 为根的子树中,不匹配 $ u $ 所能得到的最大匹配数,$ f[u][1] $ 表示在以 $ u $ 为根的子树中,u已经匹配了所等得到的最大匹配数
设 $ g[u][0/1] $ 分别对应其方案数
转移方程:
f[u][0]=max(f[v][0],f[v][1]);
f[u][1]=max(f[v][1],f[u][0]+f[v][0]+1);
if(f[v][0]==f[v][1]) g[u][0]*=g[v][1]+g[v][0] else g[u][0]*=max(g[v][0],g[v][1]);证明: $ f[u][1] \ge f[u][0] $
我们假设 $ u $ 点的边最长的子节点为 $ v $ ,设最长边数为 $ x $
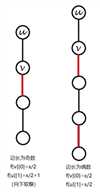
嗯......(上图的 $ f[v][0] $ 应该全都是 $ f[u][0] $ ,凑活着看吧......)证明完毕
用证明改进方程,细节看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
struct num{
int len,a[1000];
void out(){
for(int i=len;i;--i) printf("%d",a[i]);
puts("");
}
}g[1005][2];
num operator +(num x,num y){
int len=max(x.len,y.len);
for(int i=1;i<=len;++i){
x.a[i]+=y.a[i];
x.a[i+1]+=x.a[i]/10;
x.a[i]%=10;
}
if(x.a[len+1]) ++len;
x.len=len;
return x;
}
num operator *(num x,num y){
num c; memset(c.a,0,sizeof(c.a));
int len=x.len+y.len-1;
for(int i=1;i<=x.len;++i)
for(int j=1;j<=y.len;++j)
c.a[i+j-1]+=x.a[i]*y.a[j];
for(int i=1;i<=len;++i){
c.a[i+1]+=c.a[i]/10;
c.a[i]%=10;
}
if(c.a[len+1]) ++len; c.len=len;
return c;
}
vector<int>e[1005];
int f[1005][2];
void dp(int u){
g[u][1].len=g[u][0].len=1;
g[u][1].a[1]=g[u][0].a[1]=1;
for(int i=0;i<e[u].size();++i){
int v=e[u][i];
dp(v);
if(f[u][1]){
f[u][1]+=f[v][1];
if(f[v][0]^f[v][1]) g[u][1]=g[u][1]*g[v][1];
else g[u][1]=g[u][1]*(g[v][0]+g[v][1]);
}
//为什么是如果f[u][1]非空呢
//因为如果当f[u][1]为空时,我们是要默认让u点去匹配的
//所以会先执行f[u][1]=f[u][0]+f[v][0]+1
int tmp=f[u][0]+f[v][0]+1;
if(tmp>f[u][1]){
f[u][1]=tmp; g[u][1]=g[u][0]*g[v][0];
} else if(tmp==f[u][1])
g[u][1]=g[u][1]+g[u][0]*g[v][0];
//f[u][0]在f[u][1]之后更新
//是因为上一个f[u][1]=f[u][0]+f[v][0]+1时,f[u][0]不应该保护不匹配v的答案
f[u][0]+=f[v][1];
if(f[v][0]^f[v][1]) g[u][0]=g[u][0]*g[v][1];
else g[u][0]=g[u][0]*(g[v][0]+g[v][1]);
}
if(!f[u][1]){ g[u][1].len=1; g[u][1].a[1]=0; }
}
int n,m;
int main(){
scanf("%d",&n);
for(int u,i=1;i<=n;++i){
scanf("%d %d",&u,&m);
for(int v,j=1;j<=m;++j){ scanf("%d",&v); e[u].push_back(v); }
}
dp(1);
printf("%d\n",max(f[1][0],f[1][1]));
if(f[1][1]^f[1][0]){
if(f[1][1]>f[1][0]) g[1][1].out();
else g[1][0].out();
} else (g[1][1]+g[1][0]).out();
return 0;
}标签:转移 数据 height puts ceo ref and 最大 处理
原文地址:https://www.cnblogs.com/PotremZ/p/9444457.html