标签:专用 表格 情况 code 方式 nbsp 广搜 names ADG
考虑将如此安排在一个 3 x 3 行列中的九个时钟:
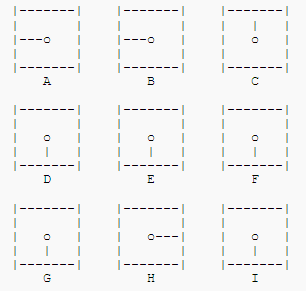
目标要找一个最小的移动顺序将所有的指针指向12点。下面原表格列出了9种不同的旋转指针的方法,每一种方法都叫一次移动。选择1到9号移动方法,将会使在表格中对应的时钟的指针顺时针旋转90度。
移动方法 受影响的时钟
1 ABDE
2 ABC
3 BCEF
4 ADG
5 BDEFH
6 CFI
7 DEGH
8 GHI
9 EFHI
Example

很明显的广搜。由于只有3,6,9,12这4个数字(不然怎么转回去?),那么先离散化,就变成了1,2,3,4四个数字,要把这4个数字都变为4。
将每种变换方式的表打出来,再广搜+判重(9维数组水过),输出路径即可。
#include <cstdio> #include <iostream> #include <map> using namespace std; const int d[][10]={{},{1,2,4,5},{1,2,3},{2,3,5,6},{1,4,7},{2,4,5,6,8},{3,6,9},{4,5,7,8},{7,8,9},{5,6,8,9}}; //变换情况 const int num[]={0,4,3,4,3,5,3,4,3,4}; //每种情况变换时钟的个数 int head,tail,state[300001][10],father[300001],z[300001]; bool p[5][5][5][5][5][5][5][5][5]; //判重专用 bool inmap(int y) //判重 { if (p[state[y][1]][state[y][2]][state[y][3]][state[y][4]][state[y][5]][state[y][6]][state[y][7]][state[y][8]][state[y][9]]) return true; p[state[y][1]][state[y][2]][state[y][3]][state[y][4]][state[y][5]][state[y][6]][state[y][7]][state[y][8]][state[y][9]]=1; return false; } void find(int x) //递归输出路径 { if (father[x]!=0) find(father[x]); printf("%d ",z[x]); return; } bool check(int x) //判断是否达成目标 { for (int i=1;i<=9;i++) if (state[x][i]!=4) return false; return true; } void bfs() { do { head++; for (int i=1;i<=9;i++) { tail++; for (int j=1;j<=9;j++) state[tail][j]=state[head][j]; for (int j=0;j<num[i];j++) state[tail][d[i][j]]=state[head][d[i][j]]%4+1; //变换 if (inmap(tail)) //已经出现过 { tail--; continue; } z[tail]=i; //记录变换方式 father[tail]=head; if (check(tail)) //达成目标 { find(tail); return; } } } while (head<tail); } int main() { head=-1; tail=0; for (int i=1;i<=3;i++) for (int j=1;j<=3;j++) { scanf("%d",&state[0][i*3-3+j]); state[0][i*3-3+j]/=3; //离散 } inmap(0); bfs(); return 0; }
标签:专用 表格 情况 code 方式 nbsp 广搜 names ADG
原文地址:https://www.cnblogs.com/hello-tomorrow/p/9451845.html