标签:序列 直接 翻转 原因 整数 模板 lct std include
题意:
给定n个点以及每个点的权值,要你处理接下来的m个操作。操作有4种。操作从0到3编号。点从1到n编号。
0:后接两个整数(x,y),代表询问从x到y的路径上的点的权值的xor和。保证x到y是联通的。
1:后接两个整数(x,y),代表连接x到y,若x到y已经联通则无需连接。
2:后接两个整数(x,y),代表删除边(x,y),不保证边(x,y)存在。
3:后接两个整数(x,y),代表将点x上的权值变成y。
1、查询、修改链上信息(min,max,sum,xor。。。。。。)
2、换根
3、动态连边,删边
4、合并两棵树
5、动态维护联通性
概念
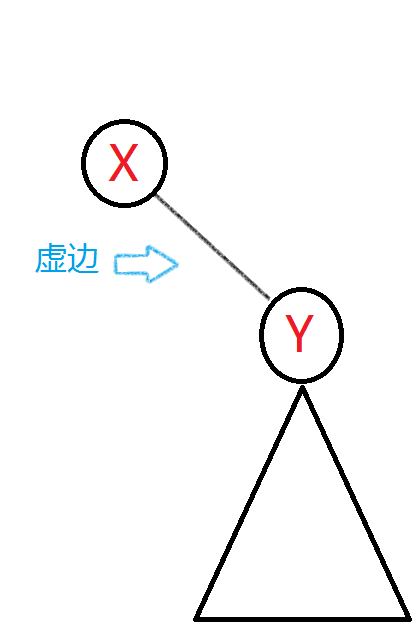
虚边:连接儿子与父亲,儿子记录父亲,父亲不记录儿子(父不认子)
实边:父子互认,互相记录
每一个节点维护一个splay!!!(常数大。。。QAQ)
性质
1、每一个splay维护从上到下按在原树中的深度
严格递增的路径,且中序遍历splay得到的每个点的深度序列
****严格递增****
2、每个节点包含且仅包含与一个splay中
3、实边在splay中,
由一棵splay指向另一节点的边为虚边
(另一节点:该splay中中序遍历最靠前的点在原树中的父亲)
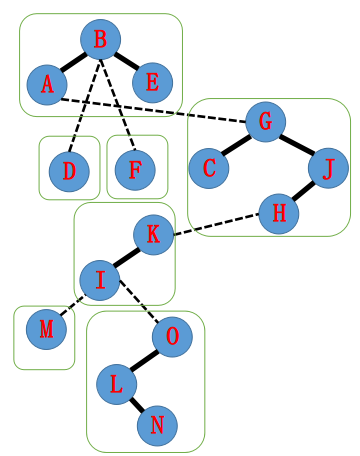
绿框中的为一个splay
里面都是实边
连接两个splay的是虚边
虚边中父亲不认孩子(透彻!!!)
4、某个点有多个儿子,只能认一个儿子拉入splay中
其它不行!(splay深度严格递增)
其它儿子父亲不认(虚边)
由儿子所属的splay的根的父节点指向该点,且父不认子。。。
1、access(基础)
作用:打通根到某一节点的实链,放在同一splay中,且此节点的深度最深!
方式:虚边变实边,然后为了维护性质,原来实边变为虚边
由根到此节点的路径上全为实边
而且由于它是最深的,他下面都是虚的!!
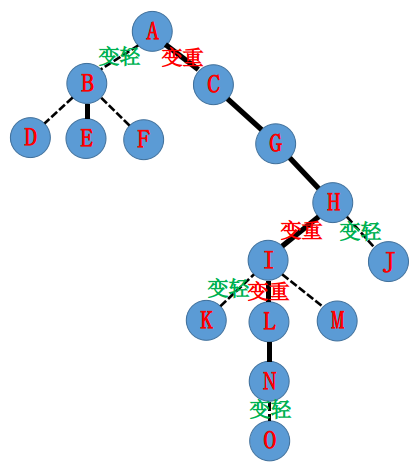
没错就是这样!
实现:
inline void access(int x) { for(int y=0;x;x=fa[y=x]) //无论实边虚边,x都记录了父亲,所以可以一直跳到根 { splay(x); //让x为当前splay的根 son[x][1]=y; //虚边变实边 push_up(x); //维护信息 } }
由于深度关系,y一定在x右边,然后让x认亲(虚变实),同时原来的实边不存在了
因为x重新认亲了,之后x继续向上。。。。。。
2、makeroot
作用:将x转变为他所在子树的根
方式:access开路(将其与根放在同一splay上)
splay它,把它转上去
****翻转左右儿子******
原因:
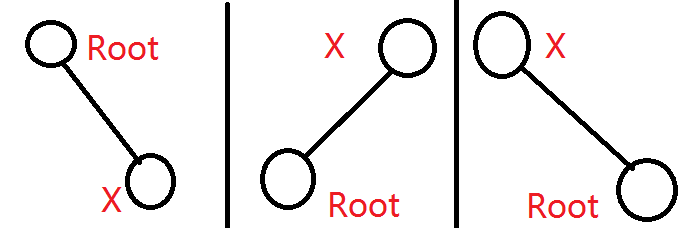
上面分别为(splay前,splay后,翻转后)
splay后,x已经成为了根,所以深度浅与原根,很明显此时不满足性质,所以翻转左右儿子!
3、split(x,y)
作用:抻出一条x-->y的路径(x和y在一棵树中)
方式:makeroot(x) 让x转到根上去
access(y) 打通y与根(x)的路径
splay(y) Splay的玄学操作,操作谁转谁
4、findroot(x)
作用:返回x所在树的根(动态判断图的联通性)
方式:access(x),splay(x) 打通x与根的路并转上去
让x一直往左跳并下放lazytag(左右儿子翻转的标记)
看上图splay前和splay后,转后x到了根的位置,但并不是我们所求的根
实际的根由于转前深度最浅到了左儿子处,因此一直往左找就一定是根
5、link(x,y)
作用:连接x,y
方式:把x转成根,直接连
inline void link(int x,int y) { makeroot(x); //x转到根 if(findroot(y)!=x) fa[x]=y; //x,y不在一棵树上,连虚边 }
6、cut(x,y)
作用:断掉x与y的边(前提是有边。。。)
实现:先makeroot(x),把x转到根
然后判断xy是否有边,有三个条件!
1、findroot(y)=x (x与y在一棵子树里,是连通的)
2、fa[x]=y (见图)
3、x没有右儿子 (见图)
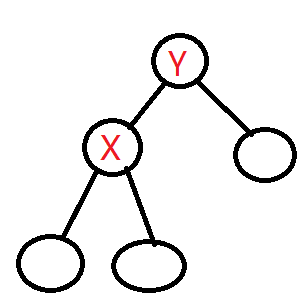
在findroot(y) 的时候会把y转到根,而之前已经把x转到了根,所以之后如图所示
x的父亲是y,这是第二个条件
但是x不能有右儿子
因为我们用splay维护深度,使深度严格递增
若x有右儿子,则实际上x与y差好几层,不可能相连。。。。(这就是第三个条件)
见代码。。。。
#include<iostream> #include<cstdio> #include<cctype> using namespace std; #define int long long #define love_nmr 0 #define olinr return #define nmr 305000 int son[nmr][2]; //记录儿子 int fa[nmr]; //记录父亲 int dis[nmr]; //维护信息(异或) int val[nmr]; //权值 bool tag[nmr]; //翻转标记 struct node //嘿嘿,手动开栈 { int st[nmr]; int tp; bool empty() { return tp==0; } void pop() { st[tp]=0; tp--; } int top() { return st[tp]; } void push(int x) { tp++; st[tp]=x; } }s; int n; int m; inline int read() { int f=1,x=0; char ch=getchar(); while(!isdigit(ch)) { if(ch==‘-‘) f=-f; ch=getchar(); } while(isdigit(ch)) { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*f; } inline void put(int x) { if(x<0) { x=-x; putchar(‘-‘); } if(x>9) put(x/10); putchar(x%10+‘0‘); } inline bool pdroot(int x) //判断x是否不是splay的根 { //若为splay的根,则他的父亲不认他QAQ olinr (son[fa[x]][0]==x||son[fa[x]][1]==x); } inline void push_up(int x)//维护信息 { dis[x]=dis[son[x][0]]^dis[son[x][1]]^val[x]; } inline void reverse(int x) //左右儿子翻转 { int t=son[x][0]; son[x][0]=son[x][1]; son[x][1]=t; tag[x]^=1; } inline void push_down(int x) //标记下放 { if(!tag[x]) olinr; if(son[x][0]) reverse(son[x][0]); if(son[x][1]) reverse(son[x][1]); tag[x]=0; } inline void rotate(int x) //splay { int y=fa[x]; int z=fa[y]; bool xx=(son[y][1]==x); bool yy=xx^1; if(pdroot(y)) son[z][son[z][1]==y]=x; fa[x]=z; fa[y]=x; fa[son[x][yy]]=y; son[y][xx]=son[x][yy]; son[x][yy]=y; push_up(y); push_up(x); } inline void splay(int x) //splay { int y=x; s.push(y); while(pdroot(y)) //维护信息 { y=fa[y]; s.push(y); } while(!s.empty()) { push_down(s.top()); s.pop(); } while(pdroot(x)) { int y=fa[x]; int z=fa[y]; if(pdroot(y)) { if((son[y][1]==x)^(son[z][1]==y)) rotate(x); else rotate(y); } rotate(x); } push_up(x); } inline void access(int x) { for(int y=0;x;x=fa[y=x]) //无论实边虚边,x都记录了父亲,所以可以一直跳到根 { splay(x); //让x为当前splay的根 son[x][1]=y; //虚边变实边 push_up(x); //维护信息 } } inline void makeroot(int x) { access(x); //为实现目的,先开路 splay(x); //路通了,转上去 reverse(x); //翻转!!!(维护性质) } inline void split(int x,int y) { //x,y在一棵子树上 makeroot(x); //把x转到根上 access(y); //打通y与根(x) splay(y); //玄学操作。。。 } inline int findroot(int x) { access(x); //开路 splay(x); //转上去 while(son[x][0]) //根最浅,所以向左找根 { push_down(x); //标记下放 x=son[x][0]; } return x; } inline void link(int x,int y) { makeroot(x); //x转到根 if(findroot(y)!=x) fa[x]=y; //x,y不在一棵树上,连虚边 } inline void cut(int x,int y) { makeroot(x); //x转到根 if(findroot(y)==x&&fa[x]==y&&!son[x][1]) //3个条件 { fa[x]=son[y][0]=0; //父子分离(残忍QAQ》 push_up(y); } } signed main() { n=read(); m=read(); int flag,x,y; for(int i=1;i<=n;i++) val[i]=read(); for(int i=1;i<=m;i++) { flag=read(); x=read(); y=read(); if(flag==0) { split(y,x); put(dis[x]); putchar(‘\n‘); continue; } if(flag==1) { link(x,y); continue; } if(flag==2) { cut(y,x); continue; } if(flag==3) { splay(x); val[x]=y; continue; } } olinr love_nmr; }
标签:序列 直接 翻转 原因 整数 模板 lct std include
原文地址:https://www.cnblogs.com/olinr/p/9455411.html