JZ模拟赛 8.10

Solution：

对于所有数据，不能直接乘。考虑质因数分解。

n根号n分解a[i]，把所有的a[i]指数相加，就是p的质因数分解。

p=2^q1*3^q2*5^q3....

m的阶乘质因数分解至少有q1个2，q2个3。。。

m的阶乘有多少个质因子2呢？

[m/2]+[m/2^2]+[m/2^3]....([]是下取整）

对于3、5同理

所以，就二分一个m，找一下阶乘中所有质数指数是几，大于qi可能是答案。

复杂度：n根号n + log(long long)*（小于100000质数个数，数量小于10000个）*log_pim

T2：

Description

       小S是一个爱锻炼的孩子，他在放假期间坚持在A公园练习跑步。
      但不久后，他就开始为在重复的地点练习感到厌烦了，他就打算去B公园跑步。
      但是小S由于没有去过B公园，他不知道B公园是否适合练习跑步，又不知道在B公园怎样跑是最优的。所以小S就去B公园进行了一番勘测。
      小S在进行了一番勘测后，画出了一张地图，地图每一个位置上都辨识了小S到达该位置后不能往哪一个方位移动。其中有5种表示的符号：“U”代表不能向上移动，“D”代表不能向下移动，“L”代表不能向左移动，“R”代表不能向右移动，如果该位置有障碍物，小S到达那里后无法继续训练，就用“S”来代表。整个公园共有n行m列，小S会从第1行第1列出发，到第n行第m列结束他的练习。
      现在小S想要知道，从起点（即第1行第1列）到终点（第n行第m列），途中最少要改变几次方向（即上一次移动的方向和这一次移动的方向不一样）？
      注意：小S如在训练途中离开公园（即地图范围），则算是结束训练。

　　n,m<=500

Solution：

bfs爆搜即可。加一个最优性剪枝。

T3：

2018年1月31日，152年一遇的超级大月全食在中国高空出现（没看到的朋友真是可惜），小B看到月食，便对月球的轨道产生了兴趣。他上网查重力加速度的公式，公式如下：


就在这个时候，他想到了一个跟这个差不多的问题，那就是对于以下公式：

已知n和k，求这n个正整数在都不大于m的情况下有多少种选择方式，使得v为与k互质正整数？

所以用一下乘法原理，就是乘上f[1][num[a[j]/a[k]]] num表示，这个约数是k的第几个约数。

就是填一个数，使得和k的gcd是第a[j]/a[k]个因数的方案数。

（显然，a[j]/a[k]是k的一个因数，所以可以直接放进f[][]里表示。）

所以，我们要预处理f[1][p]，

类似longge的问题，（我的方法和网上的不一样）

[SDOi2012]longge的问题

直接枚举k的因子，然后容斥即可。

最后dp一下。

发现，3000*（因数个数）^2 会TLE。

那么，因为转移的时候，a[j]%a[k]==0，所以a[k]是a[j]的因数，可以预处理a[j]的所有也是k的因数的因数。

也可以，在枚举的时候，直接枚举到根号a[j]即可，另一半直接算出来。

A组：

T1：

旅行 

悠悠岁月，不知不觉，距那传说中的pppfish晋级泡泡帝已是过 去数十年。数十年 中，这颗泡泡树上，也是再度变得精彩，各种泡泡 天才辈出，惊艳世人，然而，似乎 不论后人如何的出彩，在他们的头 顶之上，依然是有着一道身影而立。 泡泡帝，pppfish。 现在，pppfish即将带着被自己收服的无数个泡泡怪前往下一个 空间，而在前往下 一个空间的道路上，有N个中转站，和M条空间虫洞连接中转站（双向通道，可有重 边，可有环），然而，通过虫洞 是要一定的条件的，pppfish将手下所有泡泡怪编号为 1，2 … +∞,对于每个空间虫洞，有两个值L和R，表示此虫洞只允许编号从L到 R的泡 泡怪通过，pppfish现在在1号中转站，他想带尽可能多的泡 泡怪到达N号中转站，于是 pppfish找到了机智的你，希望你告诉 他最多可以带多少个泡泡怪，同时他还想知道所 有泡泡怪的编号（若 有多组解取字典序最小的一组 )

Solution：

枚举左端点，二分右端点，然后并查集判断联通？logle6*1e6*3000不行。

但是，最终的L，R必定是出现过的l，r！！！！只有3000个！！

所以，3000*log3000*3000可以过。

T2：

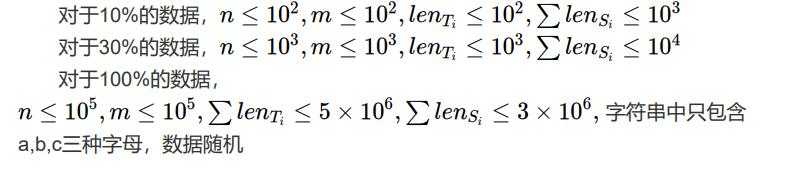
Solution:

伤心的题，差点做对。。

考虑前缀问题，一定是要trie了。把Ti放进trie里，

起初我的做法是：每个点记录是否是，是哪个si的结尾，然后，每个点开一个vector，从所有的ti的结尾的点，放进vector里，从叶子开始向上归并，到了一个有si结尾的点，最长0的长度就是相邻编号的差的最大值。

然后，MLE！！

其实不用这么麻烦了。

因为我们只要知道经过一个点相邻编号差的最大值，而我们的Ti从1~n插入，，

所以，每个trie上点维护一个las，mx值，表示上一次经过这个点的T的编号，和当前编号最大值。

每次经过一个点，就把这个编号和las做差-1尝试更新mx，开始把0，最后把n+1也加进去做个差

这样就统计出了trie上每一个点的答案。

然后不就想怎么做就怎么做？？？

插入si，到末尾直接查询！

T3：

划分 

有一个未知的序列x，长度为n。它的K-划分序列y指的是每连续K个数的和得到划分序列，y[1]=x[1]+x[2]+....+x[K]，y[2]=x[K+1]+x[K+2]+....+x[K+K]....。若n不被K整除，则y[n/K+1]可以由少于K个数加起来。比如n=13，K=5，则y[1]=x[1]+...+x[5]，y[2]=x[6]+....+x[10]，y[3]=x[11]+x[12]+x[13]。若小A只确定x的K[1]划分序列以及K[2]划分序列....K[M]划分序列的值情况下，问她可以确定x多少个元素的值。

【输入样例1】
3 1
2
【输入样例2】
6 2
2 3
【输入样例3】
123456789 3
5 6 9

【输出样例1】
1
【输出样例2】
2
【输出样例3】
10973937