标签:log inf src 问题 .com abi ros tin info
据说在费曼死后,人们在他生前的黑板上拍到如图画片,在左上角有道:What i cannot create ,I do not understand. Generative models,就是在做创造的事情。

这是目前的主要方法。

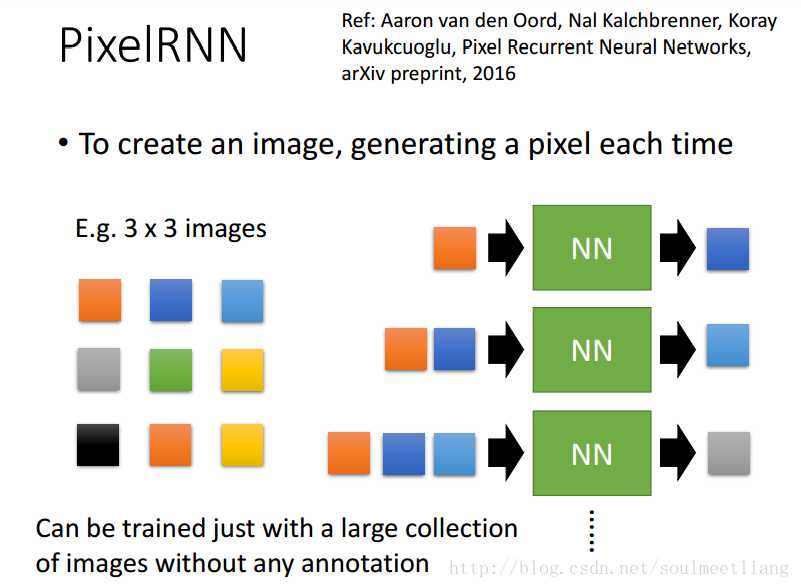
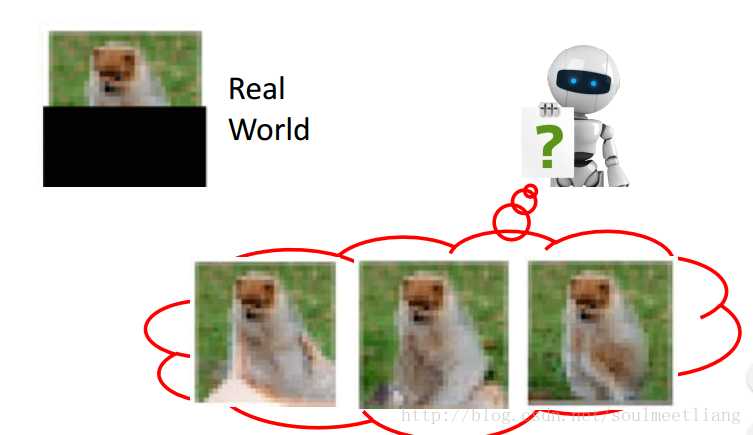
每次生成一个像素,用这样的方法,没有任何注释可以训练就有一大堆图像,效果还不错。下边是某一个实例:
回忆Auto-encoder方法,如果随机生成一个向量code输出一张图片就是在create了,但是发现这样做的performance并不很好,而Variational Autoencoder会好很多。
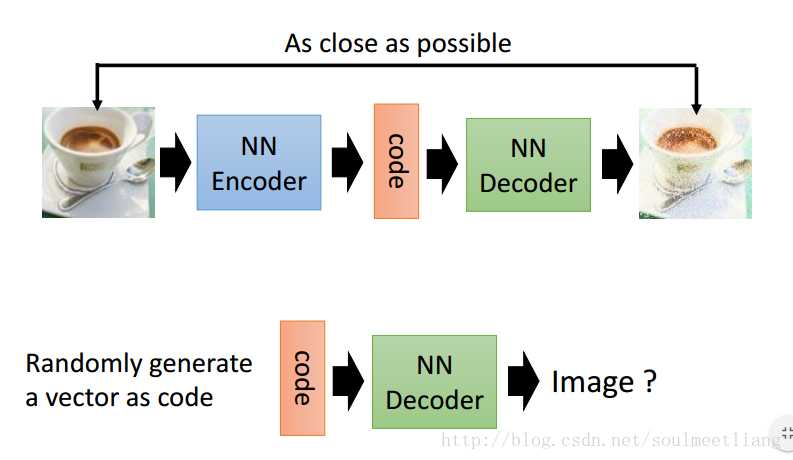
VAE结构与Auto-encoder很像
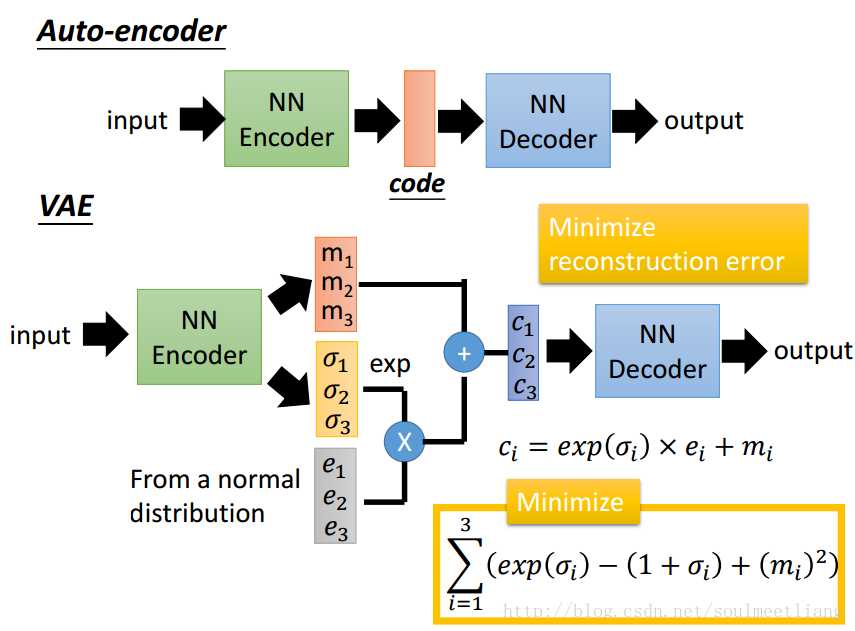
需要minimize两处。 VAE,能通过code来控制产生的结果。 比如我们固定住8维,改变其中的两维向量,看他们生成的图像变化趋势,从而得到当前维度控制结果产生的规律。
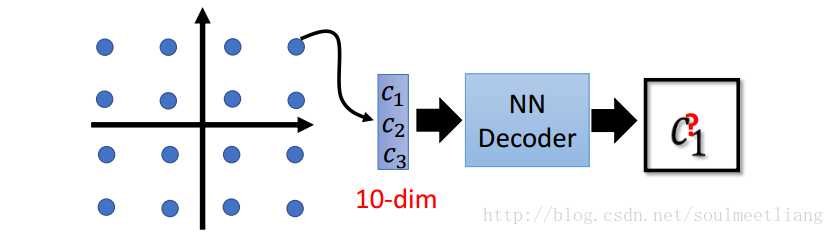
效果: 如下图,右上角站立,左下角平躺。

也可以让VAE write poetry:
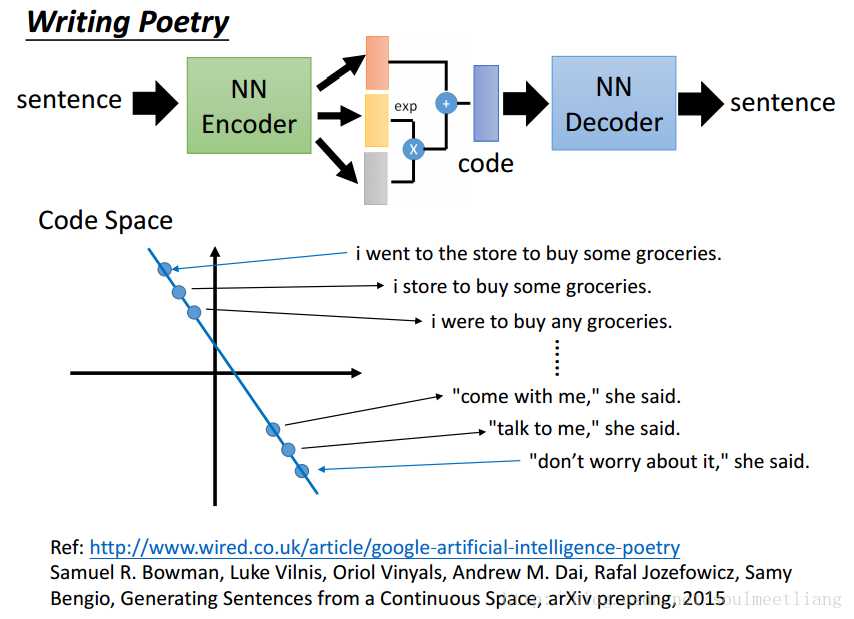
Why VAE?-->用VAE,从code space上去sample一个code,能得到一个比较好的image,而auto encoder可能得不到。
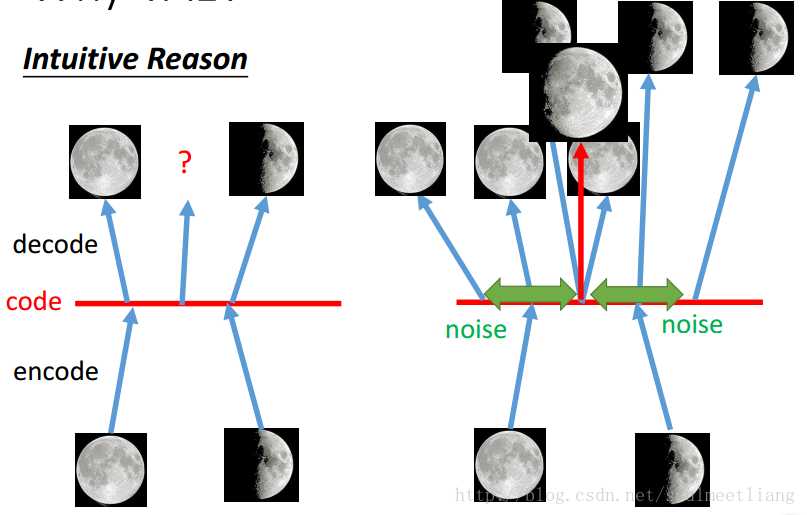
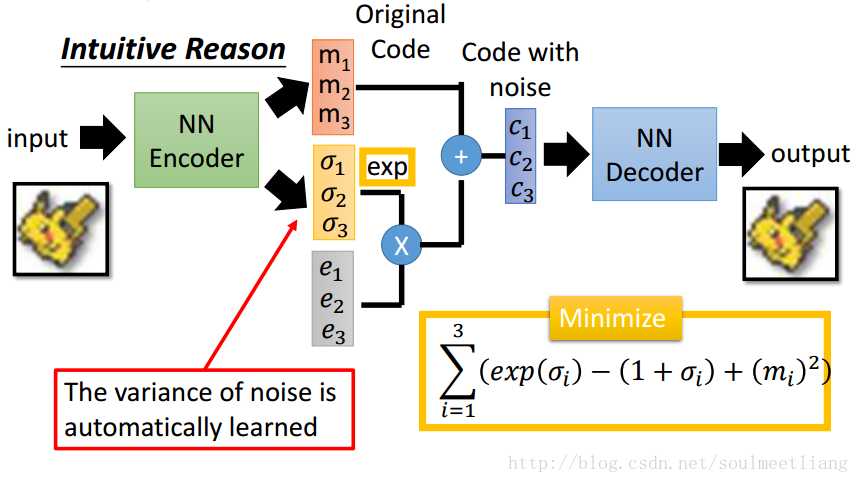
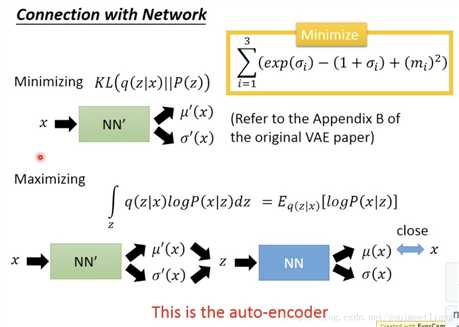
将code加上了noise,而variance决定了noise的大小,variance是train出来的。variance要做一些限制,否则就会是0,所以就要用Minimize。
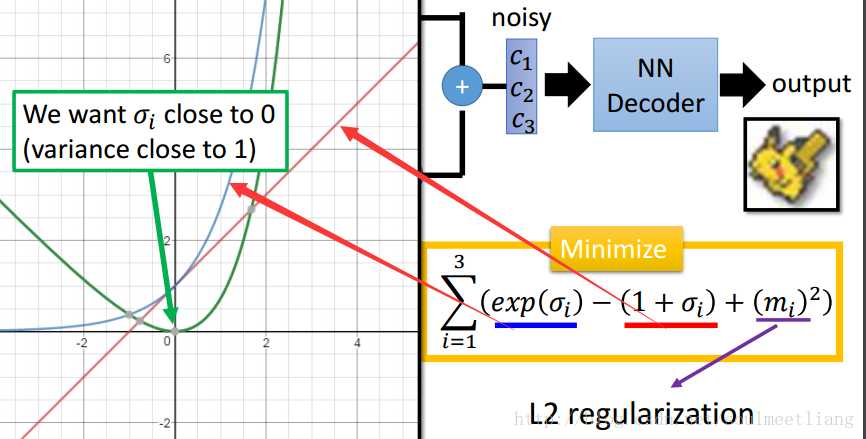
以上是直观的解释,那么回到我们要解决的问题,即Estimate the probability distribution
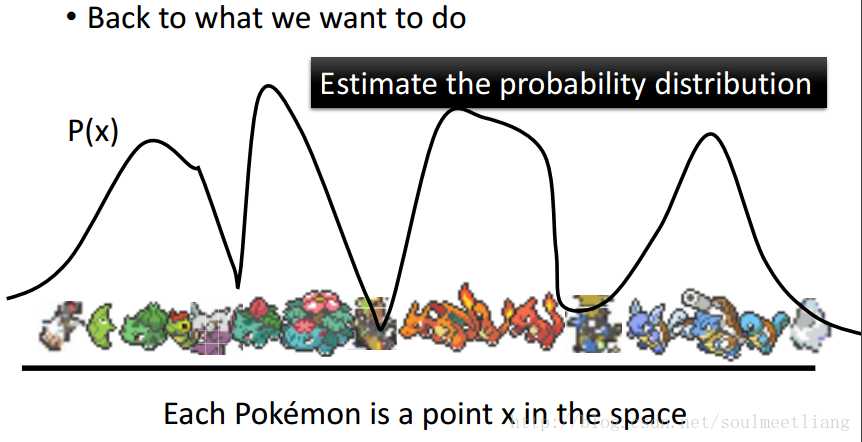
那么怎么来Estimate the probability distribution呢?可以用Gaussion Mixtrue Model 。怎样从Gaussian Mixture Model 里sample一个data呢? 首先有一个multinomial distribution,先决定sample 其中的哪一个Gaussian,用m表示。有了m,就可以找到μ和Σ,然后可以sample出一个x。
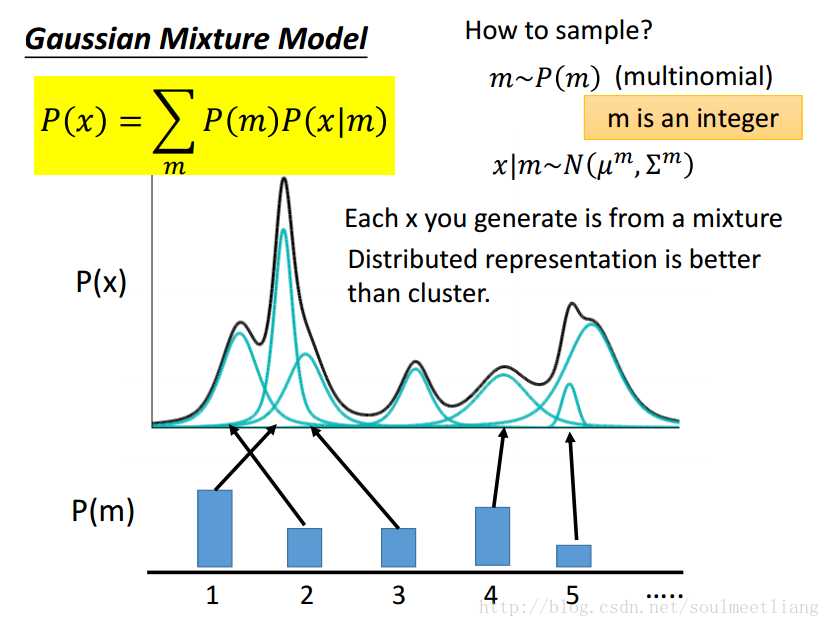
也就是说每一个你生成的x并不属于某一个class或cluster,而是它有一个vector来描述他所描述的不同对象的特性,所以,VAE其实就是Gaussian Mixture Model的distribute representation的版本。 先sample一个 z ,假设μ 和 σ都分别来自函数μ(z) 和 σ(z),在z的space里,每一个点都有可能被sample到,只是可能性有大小m,z上的每一个点都可能被sample到并对应着无穷多个gaussian,那么function该怎么找呢?那么可以说NN就是function,训练出这个NN就ok啦。
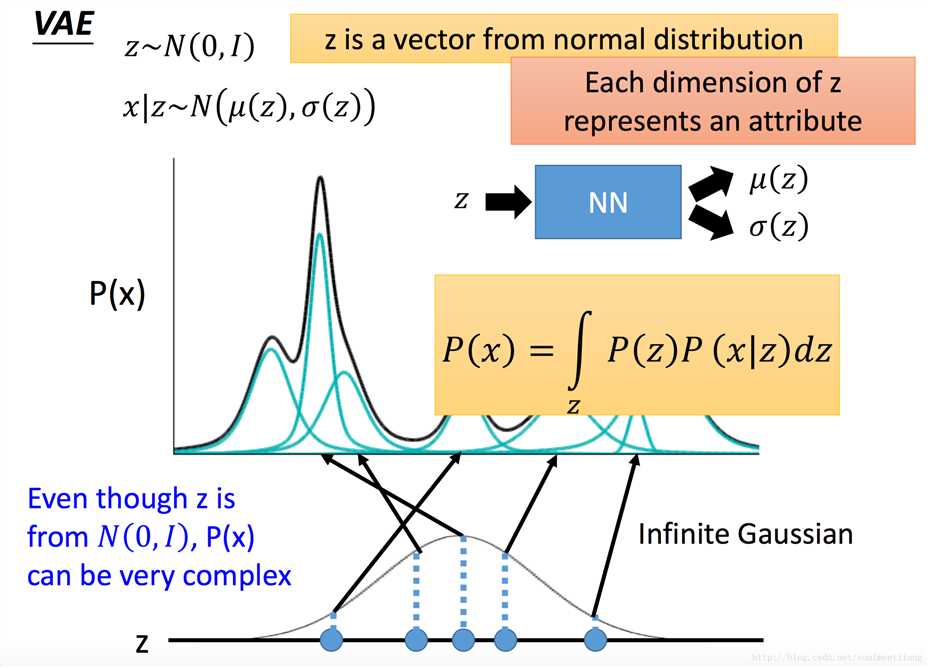
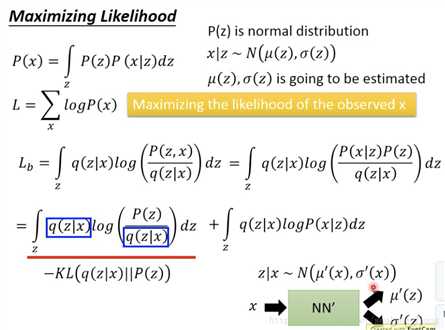
对gaussian的假设是很随意的,因为NN都能被训练适应。现在手上已经有了一批image x,maximize已有image的L。
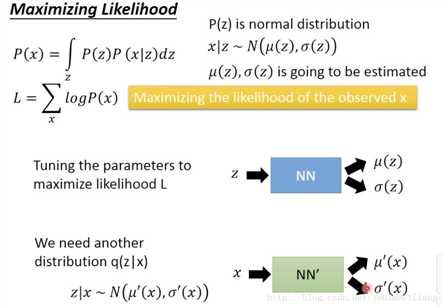
上面的NN其实就是decoder,下面的是encoder。那么那么logP(x)怎么求呢?
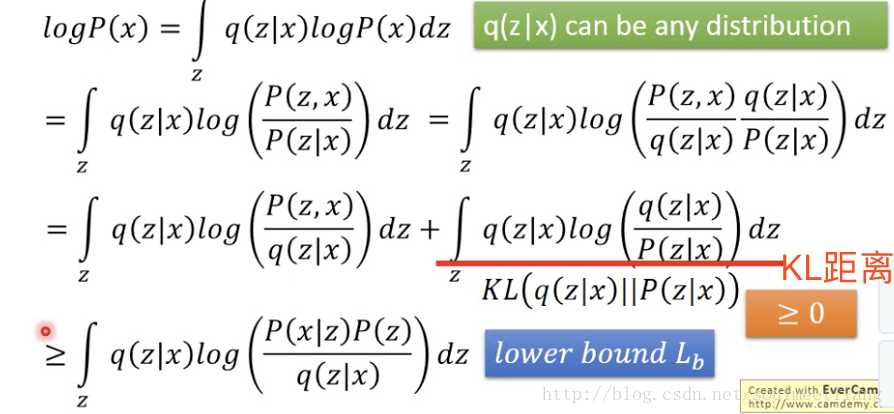
思想就是,likelihood = KL+Lb,logP(x)只与log(x|z)有关,无论q怎么调,图中的上线是不会变的。这时假如固定住p,调q是会使Lb一直上升,最后likelihood会和Lb非常接近,而再继续下去likelihood也会随之变大。
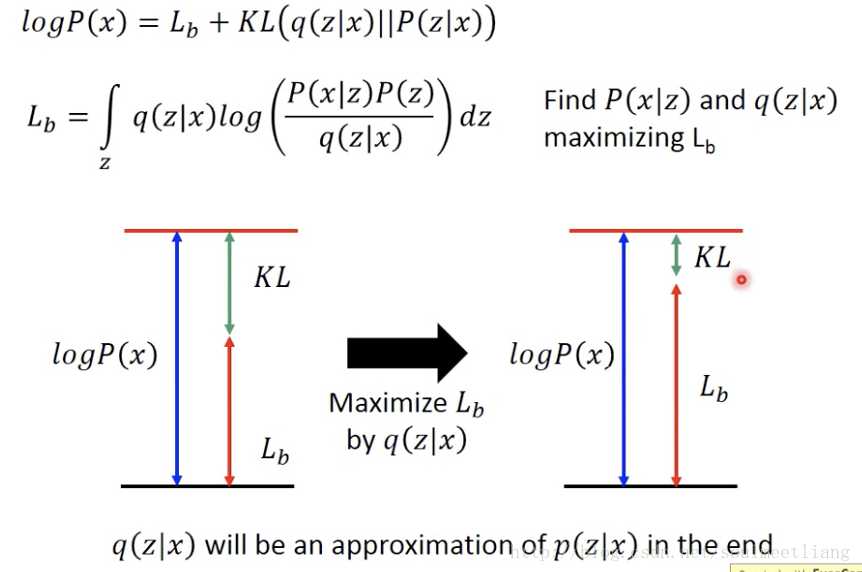
conditional VAE

Problem of VAE
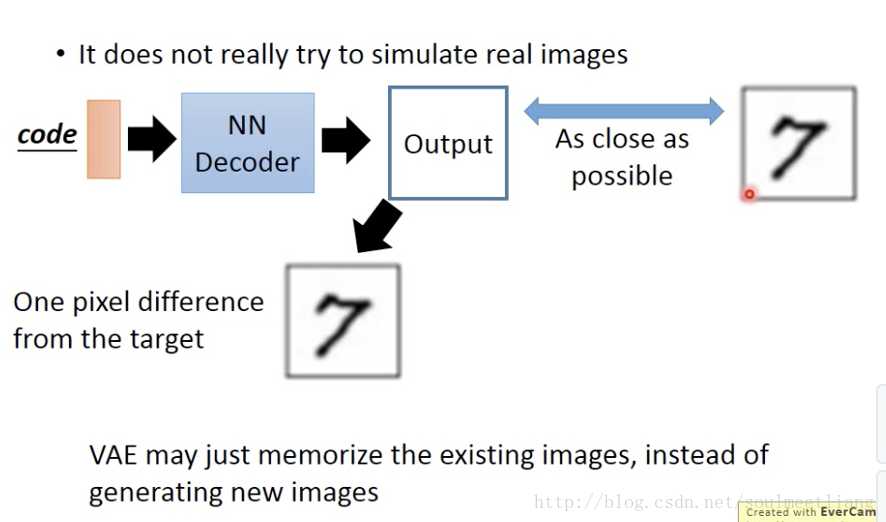
Yann LeCun’s comment的评价:

GAN的概念,有点像拟态的演化。
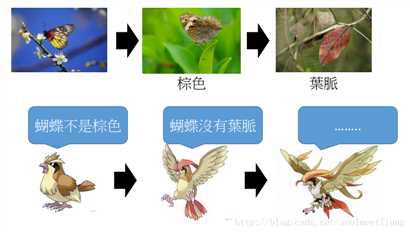
The evolution of generation,Generator演化(蝴蝶),Discriminator也跟着演化(天敌)。 需要注意的是,generator从来没有看过真正的image,它要做的就是努力骗过看过真正image的discriminator。所以generator才能产生出database中没过的image。
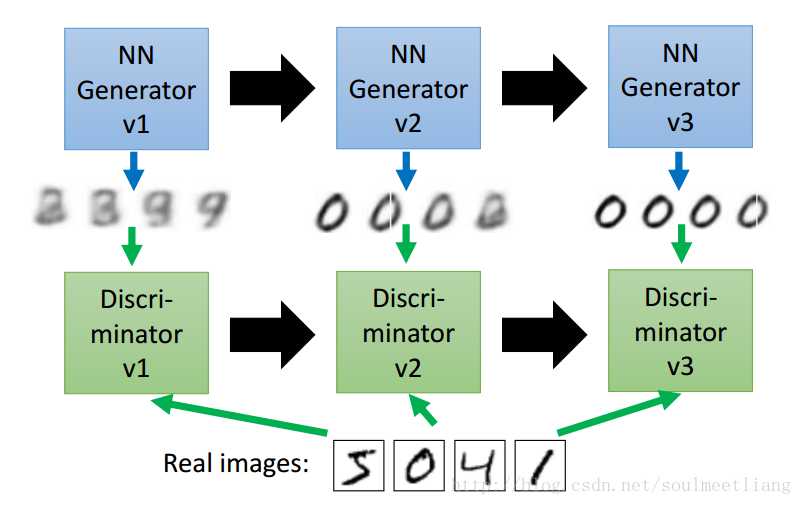
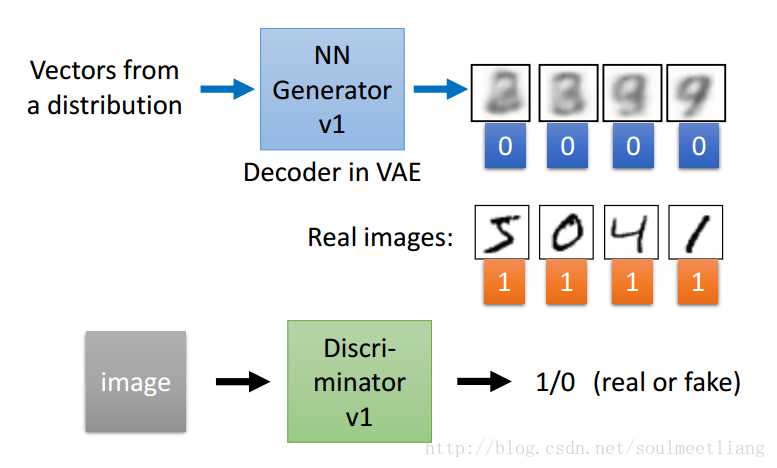
GAN - Discriminator
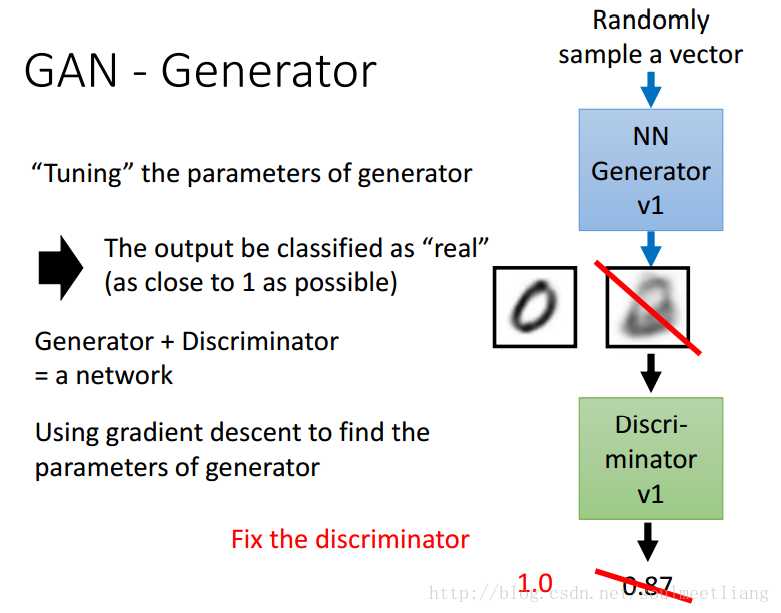
GAN - Generator
Fix the discriminator,然后去调generator的参数。
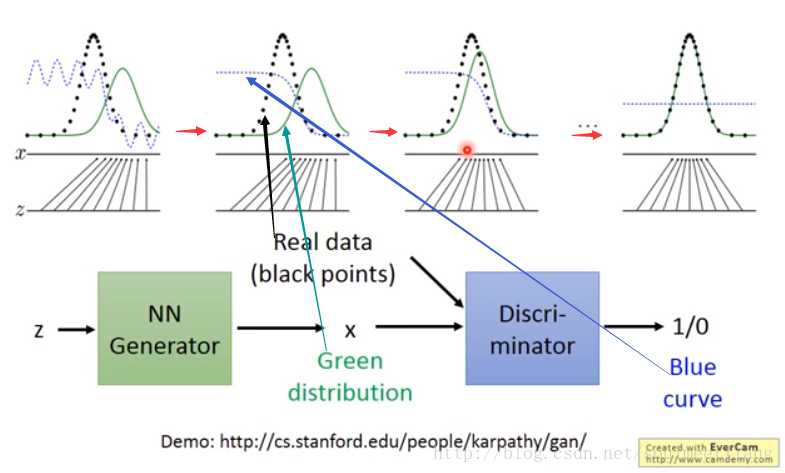
实例:GAN – Toy Example
Moving on the code space
先随机sample五个vector,然后向该方向moving,会发生很神奇的事情,比如窗变成电视,电视变成窗户。

In practical

参考:
http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2016/Lecture/VAE%20%28v5%29.pdf
https://blog.csdn.net/soulmeetliang/article/details/77461607
无监督学习:Deep Generative Mode(深度生成模型)
标签:log inf src 问题 .com abi ros tin info
原文地址:https://www.cnblogs.com/Terrypython/p/9459584.html