标签:$$ mini 研究 路径规划 man tst 控制 ast 计算机
计算机器人运动学逆解首先要考虑可解性(solvability),即考虑无解、多解等情况。在机器人工作空间外的目标点显然是无解的。对于多解的情况从下面的例子可以看出平面二杆机械臂(两个关节可以360°旋转)在工作空间内存在两个解:
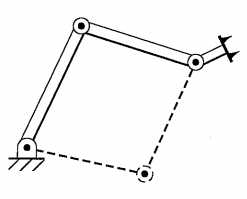
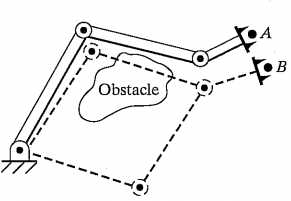
如果逆运动学有多个解,那么控制程序在运行时就必须选择其中一个解,然后发给驱动器驱动机器人关节旋转或平移。如何选择合适的解有许多不同的准则,其中一种比较合理的方法就是选择“最近”的解(the closest solution)。如下图所示,如果机器人在A点,并期望运动到B点,合理的解是关节运动量最小的那一个(A good choice would be the solution that minimizes the amount that each joint is required to move)。因此在不存在障碍物的情况下,上面的虚线构型会被选为逆解。在计算逆解时我们可以考虑将当前位置作为输入参数,这样我们就可以选择关节空间中离当前位置最近的解。
这个“最近”有多种定义方式。比如对于典型的6自由度关节型机器人来说,其前三个关节较大,后三个关节较小。因此在定义关节空间内的距离远近时要考虑给不同关节赋予不同的权重,比如前三个关节设置大权重,后三个关节设置小权重。那么在选择解的时候会优先考虑移动较小的关节而非移动大关节。而当存在障碍物时,“最近”的解的运动路径会与其发生碰撞,这时就要选择另一个运动距离较远的解("farther" solution)。因此在考虑碰撞、路径规划等问题时我们需要计算出可能存在的全部解。
逆解个数取决于机器人关节数目(the number of joints)、机器人的构型(link parameters)以及关节运动范围(the allowable ranges of motion of the joints)。决定机器人构型的D-H参数表中的非零值越多,就有越多的解存在。对于通用型6轴转动关节的机械臂来说,最多可能存在16个不同的解。下图展示了最大解的数量与非零值的连杆长度参数$a$(两关节转轴之间的最短距离,即两轴线之间公垂线的长度)的数量之间的关系:

另外机器人逆运动学求解也有多种方法,一般分为两类:封闭解(closed-form solutions)和数值解(numerical solutions)。不同学者对同一机器人的运动学逆解也提出不同的解法。应该从计算方法的计算效率、计算精度等要求出发,选择较好的解法。通常来说数值迭代解法比计算封闭解的解析表达式更慢、更耗时,因此在设计机器人的构型时就要考虑封闭解的存在性。
求解逆运动学方程的解析解(给出解的具体函数形式,从解的表达式中就可以算出任何对应值)时主要采用代数法(Algebraic solution)或几何法(Geometric solution)。下面我们先用代数法来计算平面二连杆机械臂的运动学逆解(不考虑末端关节的旋转)。正向运动学很容易得到:$$x=l_1c_1+l_2c_{12}\\y=l_1s_1+l_2s_{12}$$
将上面方程两边取平方再相加得到$x^2+y^2=l_1^2+l_2^2+2l_1l_2c_2$,消除$\theta_1$。这里用到了三角函数的和差角公式:$$c_{12}=c_1c_2-s_1s_2\\s_{12}=s_1c_2+c_1s_2$$
可以求得$\cos\theta_2$:$$c_2=\frac{x^2+y^2-l_1^2-l_2^2}{2l_1l_2}$$
为了使解存在,上式的值必须在-1~1之间,因为余弦函数$\cos x$的取值范围就是$[-1,1]$。在计算逆解时需要检查这一条件,当不满足时说明目标位置已经位于工作空间之外(the goal point is too far away for the manipulator to reach)。当目标位置$(x,y)$位于工作空间内时可以求得$\sin\theta_2$:$$s_2=\pm\sqrt{1-c_2^2}$$
为了计算$\theta_2$,可以使用Atan2函数,即:$$\theta_2=Atan2(s_2,c_2)$$
当 (x, y) 在第一象限, 0 < θ < PI/2
当 (x, y) 在第二象限 PI/2 < θ≤PI
当 (x, y) 在第三象限, -PI < θ < -PI/2
当 (x, y) 在第四象限, -PI/2 < θ < 0
$s_2$的符号有两种选择,对应的我们可以选择"elbow-up"或"elbow-down"两种不同构型。求出$\theta_2$后我们可以根据正解方程再计算出$\theta_1$。将正解方程改写为$$x=k_1c_1-k_2s_1\\y=k_1s_1+k_2c_1$$
其中$$k_1=l_1+l_2c_2\\k_2=l_2s_2$$
为了求解方程对$k_1$、$k_2$进行变量替换:$$k_1=r\cos\gamma\\k_2=r\sin\gamma$$
其中$r=\sqrt{k_1^2+k_2^2}$,$\gamma=Atan2(k_2,k_1)$
于是正解方程可写为:$$\frac{x}{r}=\cos\gamma\cos\theta_1-\sin\gamma\sin\theta_1\\ \frac{y}{r}=\cos\gamma\sin\theta_1+\sin\gamma\cos\theta_1$$
因此有:$$\cos(\gamma+\theta_1)=\frac{x}{r}\\ \sin(\gamma+\theta_1)=\frac{y}{r}$$
使用Atan2函数可得到:$\gamma+\theta_1=Atan2(y,x)$
于是第一个关节的转角$\theta_1$为:$$\theta_1=Atan2(y,x)-Atan2(k_2,k_1)=Atan2(y,x)-Atan2(l_2s_2,l_1+l_2c_2)$$ 注意之前在求解$\theta_2$时对$s_2$的符号进行了选择,这会引起$k_2$符号的变化,并影响$\theta_1$的求解。另外当x=y=0时,函数Atan2是未定义的状态,这种情况下$\theta_1$可以任意取值。
根据机构平面图,由$L_1$、$L_2$以及原点与末端之间的连线构成的三角形的余弦定理可求得$\theta_2$:$$x^2+y^2=l_1^2+l_2^2-2l_1l_2\cos(180^{\circ}+\theta_2)$$
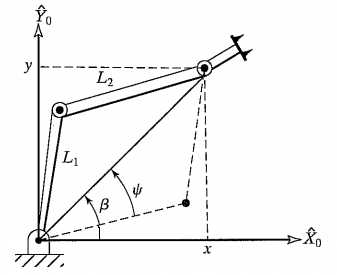
由于$\cos(180^{\circ}+\theta_2)=-\cos(\theta_2)$,可解得:$$c_2=\frac{x^2+y^2-l_1^2-l_2^2}{2l_1l_2}$$
为了保证三角形存在(三角形两边之和大于第三边),即$\sqrt{x^2+y^2}$必须小于或等于连杆长度之和$l_1+l_2$。在求逆解时需要验证是否满足这一条件,判断解的存在性。另一个可能的解(虚线所示)与之对称,$\theta_2‘=-\theta_2$
为了计算$\theta_1$,先求出图中的$\beta$和$\psi$角。$\beta$可能位于坐标系四象限中的任一象限,取决于$x$和$y$的符号,因此使用Atan2函数来求解:$\beta=Atan2(y,x)$
对$\psi$用余弦定理来计算:$$\cos\psi=\frac{x^2+y^2+l_1^2-l_2^2}{2l_1\sqrt{x^2+y^2}}$$
于是$$\theta_1=\beta\pm\psi$$
当$\theta_2<0$时取正号,$\theta_2>0$时取负号
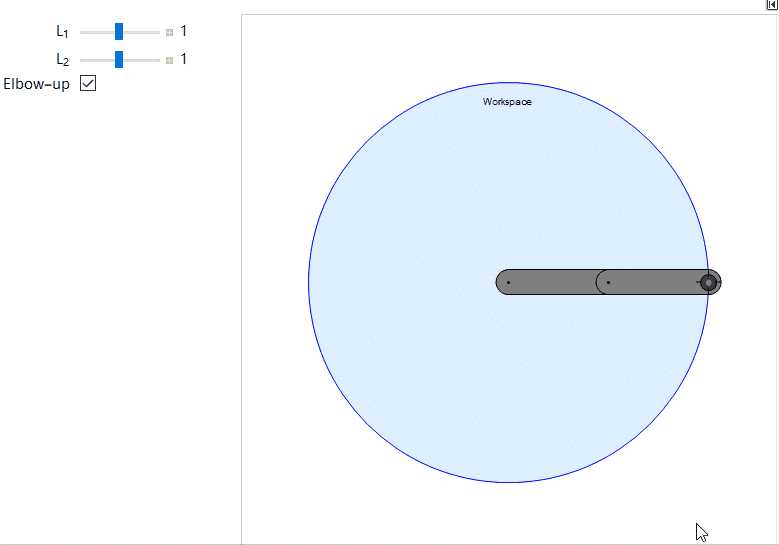
编写Mathematica代码进行平面二杆机械臂运动模拟,使用Locator来改变工作空间中机械臂末端的目标位置。


机器人运动学中的Pieper准则是:机器人的三个相邻关节轴交于一点或三轴线平行。
对于6自由度的机器人来说,运动学反解非常复杂,一般没有封闭解。在应用D-H法建立运动学方程的基础上,进行一定的解析计算后发现,位置反解往往有很多个,不能得到有效地封闭解。Pieper方法就是在此基础上进行研究发现,如果机器人满足两个充分条件中的一个,就会得到封闭解,这两个条件是:
(1)三个相邻关节轴相交于一点
(2)三个相邻关节轴相互平行(在无限远处交于一点)
现在的大多数商品化机器人都满足封闭解的两个充分条件之一。如PUMA和STANFORD机器人满足第一条件,而ASEA和MINIMOVER机器人满足第二条件。以PUMA560机器人为例,它的最后3个关节轴相交于一点。
下面考虑6自由度转动关节机器人最后三根轴交于一点的情况。根据D-H参数坐标系建立方法,这种情况下杆件坐标系{4}、{5}、{6}的原点将位于三根轴线的交汇点。该点在机器人基座标系中的齐次坐标可表示为:$$^0P_{4ORG}=_{1}^{0}T \cdot_{2}^{1}T\cdot_{3}^{2}T\cdot^3P_{4ORG}=\begin{bmatrix}x\\ y\\ z\\ 1\end{bmatrix}\tag{1}$$ 或者根据相邻杆件坐标系之间的变换关系:$$_{i}^{i-1}\textrm{T}=\begin{bmatrix}c\theta_i & -s\theta_i & 0 & a_{i-1}\\ s\theta_ic\alpha_{i-1} & c\theta_ic\alpha_{i-1} & -s\alpha_{i-1} & -s\alpha_{i-1}d_i\\ s\theta_is\alpha_{i-1} & c\theta_is\alpha_{i-1} & c\alpha_{i-1} & c\alpha_{i-1}d_i\\ 0 & 0 & 0 & 1\end{bmatrix}\tag{2}$$ 可以得到:$$^0P_{4ORG}=_{1}^{0}T \cdot_{2}^{1}T\cdot_{3}^{2}T\begin{bmatrix}a_3\\ -d_4s\alpha_3\\ d_4c\alpha_3\\ 1\end{bmatrix}\tag{3}$$ 或:$$^0P_{4ORG}=_{1}^{0}T \cdot_{2}^{1}T\begin{bmatrix}f_1(\theta_3)\\ f_2(\theta_3)\\ f_3(\theta_3)\\ 1\end{bmatrix}\tag{4}$$ 其中:$$\begin{bmatrix}f_1\\ f_2\\ f_3\\ 1\end{bmatrix}=_{3}^{2}T\begin{bmatrix}a_3\\ -d_4s\alpha_3\\ d_4c\alpha_3\\ 1\end{bmatrix}\tag{5}$$ 将参数带入$_{i}^{i-1}T$矩阵得到$_{3}^{2}T$,可以列出$f_1$、$f_2$、$f_3$的表达式:$$\begin{align*}f_1&=a_3c_3+d_4s\alpha_3s_3+a_2\\ f_2&=a_3c\alpha_2s_3-d_4s\alpha_3c\alpha_2c_3-d_4s\alpha_2c\alpha_3-d_3s\alpha_2 \\ f_3&=a_3s\alpha_2s_3-d_4s\alpha_3s\alpha_2c_3+d_4c\alpha_2c\alpha_3+d_3c\alpha_2\end{align*}\tag{6}$$ 再根据 $_{1}^{0}T$和 $_{2}^{1}T$我们可以得到$$^0P_{4ORG}=\begin{bmatrix}c_1g_1-s_1g_2\\ s_1g_1+c_1g_2\\ g_3\\ 1\end{bmatrix}\tag{7}$$ 其中$$\begin{align*}g_1&=c_2f_1-s_2f_2+a_1 \\ g_2&=s_2c\alpha_1f_1+c_2c\alpha_1f_2-s\alpha_1f_3-d_2s\alpha_1 \\ g_3&=s_2s\alpha_1f_1+c_2s\alpha_1f_2+c\alpha_1f_3+d_2c\alpha_1 \end{align*}\tag{8}$$ 接下来我们计算$^0P_{4ORG}$坐标的平方和:$$r=x^2+y^2+z^2=g_1^2+g_2^2+g_3^2\tag{9}$$ 根据方程(8)有:$$r=f_1^2+f_2^2+f_3^2+a_1^2+d_2^2+2d_2f_3+2a_1(c_2f_1-s_2f_2)\tag{10}$$ 再接着进行变量替换消除对关节转角$\theta_1$的依赖,令:$$\begin{align*}r&=(k_1c_2+k_2s_2)2a_1+k_3\\z&=(k_1s_2-k_2c_2)s\alpha_1+k_4 \end{align*}\tag{11}$$ 其中:$$\begin{align*}k_1&=f_1\\k_2&=-f_2\\k_3&=f_1^2+f_2^2+f_3^2+a_1^2+d_2^2+2d_2f_3\\k_4&=f_3c\alpha_1+d_2c\alpha_1\end{align*}\tag{12}$$ 下面考虑根据方程(11)求解$\theta_3$,分下面3种情况:
1. 如果$a_1=0$,则$r=k_3$,由于$r$是已知量,等式右边的$k_3$是$\theta_3$的函数。用三角函数万能公式进行变量替换后可求解$\theta_3$
2. 如果$s\alpha_1=0$,则$z=k_4$,由于$z$已知,进行变量替换后可求出$\theta_3$
3. 如果条件1、2不成立,则从公式(11)中消除$s_2$和$c_2$,得到:$$\frac{(r-k_3)^2}{4a_1^2}+\frac{(z-k_4)^2}{s^2\alpha_1}=k_1^2+k_2^2\tag{13}$$ 对方程(13)进行变量替换后可求解$\theta_3$,之后可根据方程(11)求解$\theta_2$,根据方程(7)求解$\theta_1$。
最后还需要求解$\theta_4$、$\theta_5$、$\theta_6$。机械臂最后三个关节的轴线交于一点,这三个关节的转角会影响末端姿态,可以从代表末端姿态的旋转矩阵$_6^0R$中求解出$\theta_4$、$\theta_5$、$\theta_6$。在之前求解得到$\theta_1$、$\theta_2$、$\theta_3$后我们可以计算出矩阵$_4^0R|_{\theta_4=0}$,表示$\theta_4=0$时杆件坐标系{4}相对于基坐标系的姿态。从坐标系{4}到末端坐标系{6}的姿态变化由最后三根轴决定,写成矩阵变换的形式如下:$$_6^4R|_{\theta_4=0}=_4^0R^{-1}|_{\theta_4=0} \cdot_6^0R\tag{14}$$ 已知$_6^4R|_{\theta_4=0}$后最后三个关节转角可根据欧拉角与旋转矩阵之间的关系计算出来。
参考:
Introduction to Robotics - Mechanics and Control. Chapter 4 Inverse manipulator kinematics
Forward and Inverse Kinematics for Two-Link Arm
V-rep学习笔记:机器人逆运动学数值解法(The Jacobian Transpose Method)
V-rep学习笔记:机器人逆运动学数值解法(The Pseudo Inverse Method)
V-rep学习笔记:机器人逆运动学数值解法(Damped Least Squares / Levenberg-Marquardt Method)
标签:$$ mini 研究 路径规划 man tst 控制 ast 计算机
原文地址:https://www.cnblogs.com/21207-iHome/p/9452896.html