标签:了解 整型 按位运算 || 表达式 class case ... subject
1 public class Solution { 2 public int Sum_Solution(int n) { 3 4 int res=(int)(Math.pow(n, 2)+n); 5 6 res=res>>1; 7 return res; 8 9 } 10 }
也附上pow函数的算法,作为巩固
1 public class Solution { 2 public double Power(double base, int exponent) { 3 4 double res = 1; 5 6 int p = Math.abs(exponent); 7 8 while (p != 0) { 9 10 if ((p & 1) != 0) { 11 12 res *= base; 13 14 } 15 base *= base; 16 p >>= 1; 17 } 18 19 return exponent < 0 ? 1 / res : res; 20 21 } 22 }
下面这种方法是摘录过来的,运用了 逻辑运算符 &&,想法很好。
1.需利用逻辑与的短路特性实现递归终止。 2.当n==0时,(n>0)&&((sum+=Sum_Solution(n-1))>0)只执行前面的判断,为false,然后直接返回0;3.当n>0时,执行sum+=Sum_Solution(n-1),实现递归计算Sum_Solution(n)。1 public int Sum_Solution(int n) { 2 int sum = n; 3 boolean ans = (n>0)&&((sum+=Sum_Solution(n-1))>0); 4 return sum; 5 }
给自己做个笔记:
1、逻辑运算的短路特性:
(表达式1)&&(表达式2) 如果表达式1为假,则表达式2不会进行运算,即表达式2“被短路”
(表达式1)||(表达式2) 如果表达式1为真,则表达式2不会进行运算,即表达式2“被短路”
2:逻辑运算和位运算(之前真没注意二者的细致区别,好像还混用了 & &&)
位运算符
Java定义了位运算符,应用于整数类型(int),长整型(long),短整型(short),字符型(char),和字节型(byte)等类型。
位运算符作用在所有的位上,并且按位运算。假设a = 60,b = 13;它们的二进制格式表示将如下:
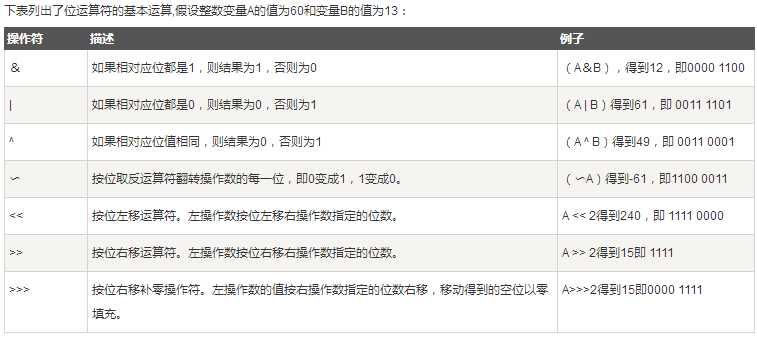
下表列出了逻辑运算符的基本运算,假设布尔变量A为真,变量B为假

标签:了解 整型 按位运算 || 表达式 class case ... subject
原文地址:https://www.cnblogs.com/Octopus-22/p/9461533.html