线性回归和 逻辑回归 的思考（参考斯坦福 吴恩达的课程）

标签：str   编写   贝叶斯   引入   ima   sub   http   取值   img   

还是不习惯这种公式的编写，还是直接上word。。。。

对上面的（7）式取log后并最大化即可得到最小二乘法，即 argmax_θ J(θ)

思考二:线性回归到逻辑回归的转变：

1） 引入逻辑回归，假设用线性回归来做分类问题，设为二分类，即y取0或1。

则会出现如下的情况：

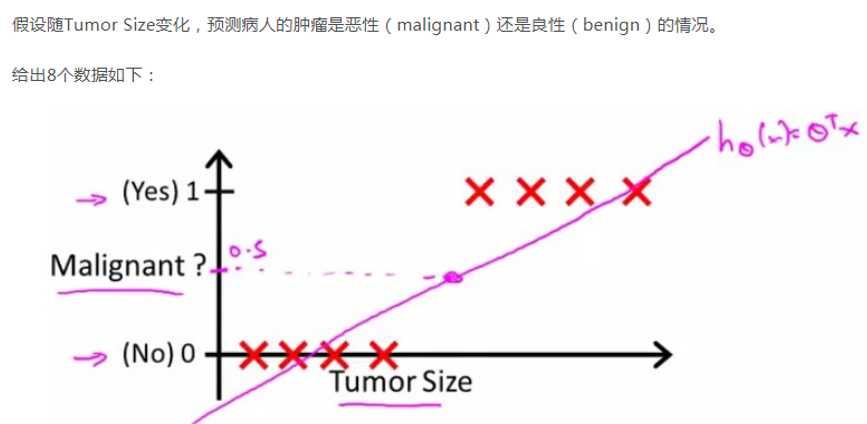
这种情况下是能很好的分类的，但若数据是如下所示呢：

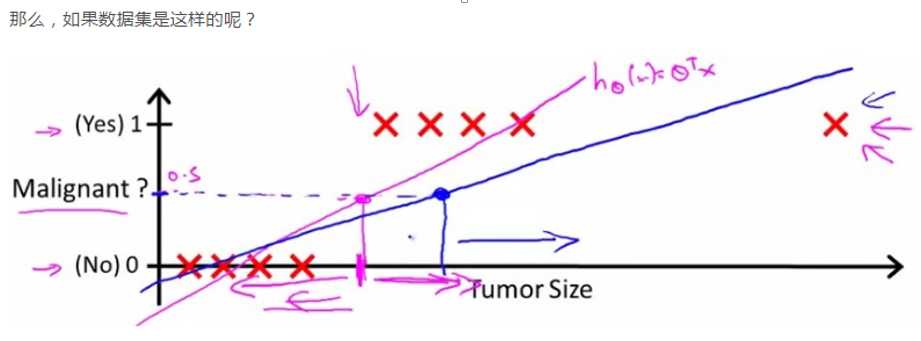
则分类很不好。

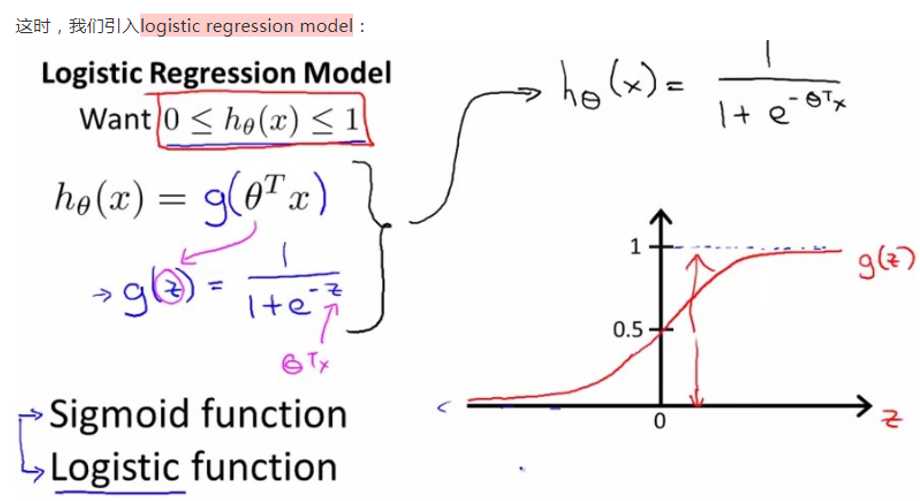
思考三：逻辑回归损失函数的得来(解释)：

    答，也是通过最大似然得到的。y的取值为0，1；则认为这是一个伯努力的分布，也称为两点的分布，则公式表示如下：

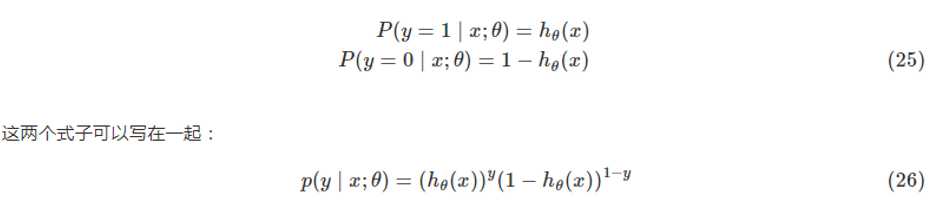
注：公式（27）最后一行的公式写错了，少了个log，正确公式应是如下：

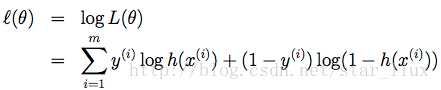
四：逻辑函数（Logistic function）或者是S形函数（Sigmoid function） 的由来：

总结：

1）算法是一个很有逻辑（严谨）的一门学科，都有因果和解释。

2）还有最大似然 法是神器，许多算法的推导都是从其开始的，若 最大似然法 加上 贝叶斯公式就更是神器啦！

参考：  线性回归、logistic回归、广义线性模型——斯坦福CS229机器学习个人总结：

　　　　https://blog.csdn.net/sinat_37965706/article/details/69204397

　　　　Stanford机器学习---第三讲. 逻辑回归和过拟合问题的解决 logistic Regression & Regularization：

　　　　https://blog.csdn.net/sinat_37965706/article/details/69204397

线性回归和 逻辑回归 的思考（参考斯坦福 吴恩达的课程）

标签：str   编写   贝叶斯   引入   ima   sub   http   取值   img   

原文地址：https://www.cnblogs.com/vincentbnu/p/9461688.html