Data Constraint
n<=100000
ai<=10^9
Output
输出一行,这个队列里从前到后的每个人的身高。如果有多个答案满足题意,输出字典序最小。如果不存在满足题意的排列,输出“impossible”(不含引号)。
Solution:
比较套路的想法。
按身高从小到大,给位置开一个线段树,该位置有,就是1,否则是0.
期初都是1,身高最小的记的数字是x,
那么,她要么在第x+1个位置,要么在n-x个位置。选择一个字典序最小的,即较靠前的位置。
把这个位置在线段树上归零。
重复这样的操作,每次在线段树上二分,找到剩余的满足的两个位置。
为什么是对的?
因为身高从小到大,考虑小的时候,别的都是比她大的,比她小的已经归位。
所以,剩余位置总是一定的情况下,前面怎么放是不影响后面的,也不影响无解情况。
所以,小的就按照字典序最小贪心了。
判断无解:线段树二分的时候,如果到了叶子节点,但是kth不为1,就是无解了。
T2:
Description
小X 是一位热爱数学的男孩子,在茫茫的数字中,他对质数更有一种独特的情感。小X 认为,质数是一切自然数起源的地方。
在小X 的认知里,质数是除了本身和1 以外,没有其他因数的数字。
但由于小X 对质数的热爱超乎寻常,所以小X 同样喜欢那些虽然不是质数,但却是由两个质数相乘得来的数。
于是,我们定义,一个数是小X 喜欢的数,当且仅当其是一个质数,或是两个质数的乘积。
而现在,小X 想要知道,在L 到R 之间,有多少数是他喜欢的数呢?
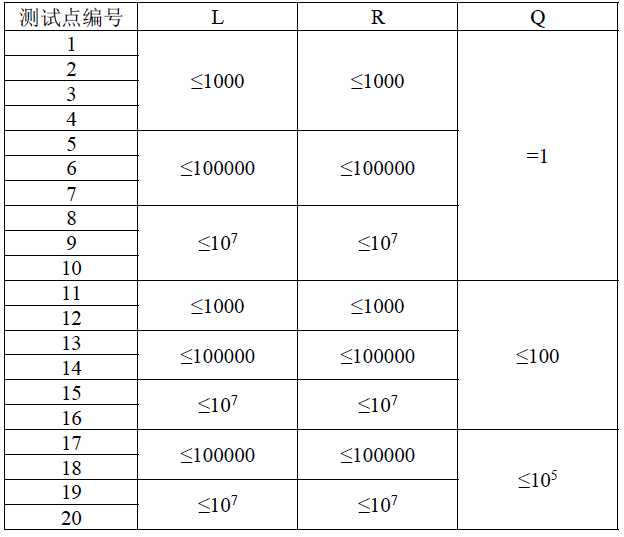
Solution:
质数好处理,关键是两个质数的乘积怎么办?
考虑线性筛的过程,每个合数只会被它的最小质因子筛一次,如果一个合数是两个质数的乘积,那么和它最小质因子相乘的数一定也是质数。
所以, 在线性筛的时候,不光记录vis,还记录这个数是不是两个质数乘积。
if(!vis[i]) has[i*pri[j]]=1 has数组就标记了合数。
然后,1e7前缀和处理一下,查询直接O(1)
或者每次二分答案也可以。
T3:
Description
nodgd写了一篇文章,自认为这是一篇好文章。nodgd的文章由??个小写英文字母组成。文章的一个子串指的是文章中的一段连续的字母,子串的长度就是这一段的字母个数。nodgd在文章中用了排比、对偶、前后照应之类的手法,所以就有很多个子串是相同或者相近的。为了向大家证明这是一篇好文章,nodgd决定给自己的文章进行评分。nodgd首先确定了一个整数??,然后统计出文章中有多少个不相同的长度为??的子串,这个数量就是文章的评分。
然而,nodgd懒得老老实实计算这个评分了,就把任务丢给了你。
Data Constraint
对于30%的数据,1≤??≤??≤200;
对于50%的数据,1≤??≤??≤2000;
对于另外20%的数据,1≤??≤50≤??≤200000;
对于100%的数据,1≤??≤??≤200000。
Solution:
裸的哈希,但是显然不会这么简单。
出题人卡哈希卡到了极致。1e9+7 1e9+9的质数都能卡到70分。更小的就更不用说了。
所以双哈希。
当一个字符串在两个set里有一次没有出现的话,就认为是一个新的字符串。
因为,可能因为取模的问题,把不同的模成了相同的。

