数据结构（四）树---树的转换

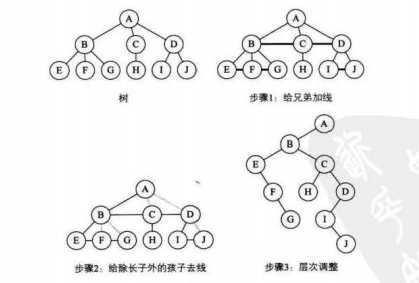
1.加线：在所有兄弟结点之间加一条连线
2.去线：对树中每个结点，只保留他与第一个长子结点的连线，删除他与其他孩子结点之间的连线
3.层次调整。以树的根节点为轴心，将整棵树顺时针旋转一定角度，使结构层次分明。
注意：第一个孩子是二叉树结点的左孩子，兄弟转换过来的孩子是结点的右孩子

转换后，根节点只有左子树，最左侧链表不改变

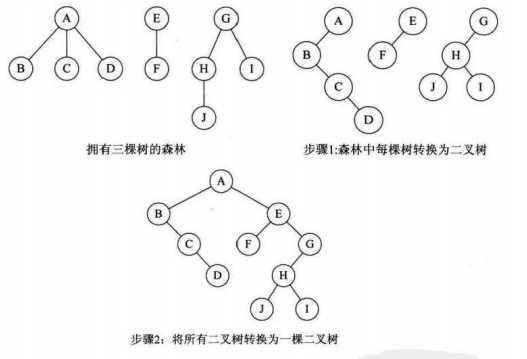
1.将每个树转换为二叉树
2.第一棵二叉树不动，从第二棵二叉树开始，依次吧后一棵二叉树的根节点作为前一棵二叉树的根节点的右子树，用线连接起来。当所有的二叉树连接起来，就得到了由森林转换而来的二叉树

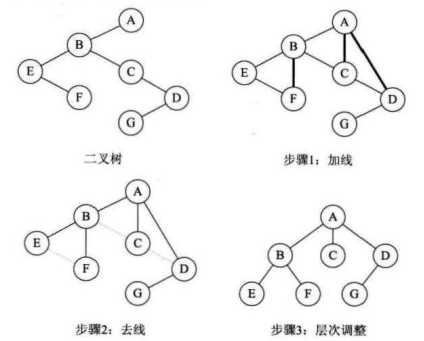
1.若某结点的左孩子存在，则将该左孩子的右孩子结点，以及该左孩子的右孩子的右孩子结点，以及...，就是左孩子的n个右孩子结点都作为此结点的孩子。将该结点与这些右孩子结点用线连接
2.去线：删除原二叉树中所有结点与其右孩子结点的连线

我们从一：知道树转二叉树只有左子树，森林转二叉树会同时存在左子树和右子树

所以判断一棵树能够转换为一棵树还是一个森林，就看这个二叉树的根节点有没有右孩子

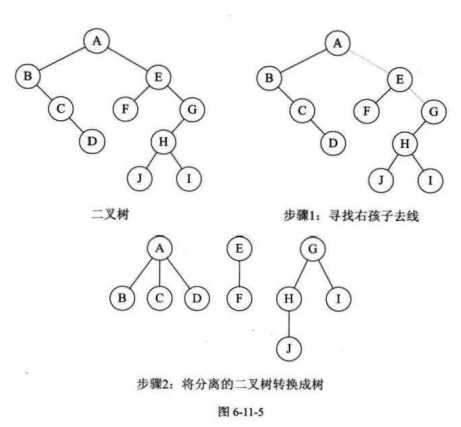
1.从根节点开始，若是右孩子存在，将右链拆开，所有的右孩子连线都删除。得到分离的二叉树。

2.再将每棵分离后的二叉树转换为树即可

先根遍历树，即先访问树的根节点，然后依次先根遍历根的每棵子树（类似于先序遍历）

后根遍历，即先依次后根遍历每棵子树，然后再访问根节点。（类似于后序遍历）

先访问森林的第一棵树的根节点，然后依次先根遍历....，再依次用同样方法遍历下一棵树....

先访问森林的第一棵树的根节点，然后依次后根遍历....，再依次用同样方法遍历下一棵树....

树，森林的前根（序）遍历和二叉树的前序遍历结果相同，树，森林的后根（序）遍历和二叉树的中序遍历结果相同

可以根据（一）和（二）轻松推出结论，然后利用这种规律，解决这些复杂的树，森林遍历问题