MATLAB 线性规划实例应用

标签：选择   开始   招聘   分析   没有   分配   生产   lag   系统   

• 线性规划

1. 线性规划函数
2. 功能：求解线性规划问题
3. 语法
   • x = linprog(f,A,b)：求解问题 min fx，约束条件为 Ax <= b
   • x = linprog(f,A,b,Aeq,beq)：求解上面的问题，但增加等式约束，即 Aeqx = beq，若没有不等式存在，则令 A= []、b = []
   • x = linprog(f,A,b,Aeq,beq,lb,ub)：定义设计变量 x 的下届 lb 和 上届 ub，使得 x 始终在该范围内，若没有等式约束，令 Aeq = []、beq = []
   • x = linprog(f,A,b,Aeq,beq,lb,ub,x0)：设置初值为 x0。该选项只适用于中型问题，默认大型算法将忽略初值
   • x = linprog(f,A,b,Aeq,beq,lb,ub,x0,options)：用 options 指定的优化参数进行最小化
   • [x,fval] = linprog(...)：返回解 x 处的目标函数值 fval
   • [x,lambda,exitflag] = linprog(...)：返回 exitflag 值，描述函数计算的退出条件
   • [x,lambda,exitflag,output] = linprog(...)：返回包含优化信息的输出变量 output
   • [x,fval,lambda,exitflag,output] = linprog(...)：将解 x 处的拉格朗日乘子返回到 lambda 参数中
4. 变量及算法：lambda 参数介绍

• • lambda 是解 x 处的拉格朗日乘子，它的属性如下
  • lambda.lower：lambda 的下届
  • lambda.upper：lambda 的上届
  • lambda.ineqlin：lambda 的线性不等式
  • lambda.eqlin：lambda 的线性等式

• • 大型优化算法：采用 LIPSOL 法，该法在进行迭代计算之前首先要进行一系列的预处理
  • 中型优化算法：linprog 函数使用的是投影法，就像 quadprog 函数的算法一样，linprog 函数使用的是一种活动集方法，是线性规划中单纯形法的变种，他通过求解另一个线性规划问题来找到初始可行解
• 线性规划问题的应用

1. 生产决策问题
   
   • 某厂生产甲、乙两种产品，已知制成一吨产品甲需用资源A 3 吨，资源B 4 $m^3$，制成每吨产品乙需用资源A 2 吨，资源B 6 $m^3$，资源C 7 个单位。若每吨产品甲和乙的经济价值分别为 7 万元和 5 万元，3 种资源的限制量分别为 80 吨、220 $m^3$ 和 230 个单位，试分析应生产这两种产品各多少吨才能使创造的总经济价值最高？
   • 这里可以令生产产品甲的数量为 $x_1$，生产产品乙的数量为 $x_2$。根据题意，代码设置如下：

     clc
     clear
     f = [-7;-5];
     A = [3 2
          4 6
         0 7];
     b = [80;220;230];
     lb = zeros(2,1);

     然后调用 linprog 函数：

     [x,fval,exitflag,output,lambda] = linprog(f,A,b,[],[],lb)

     最优化结果如下：

• • 由上可知，生产甲种产品 4.7619 吨、乙种产品 32.8571 吨可使创造的总经济价值最高，最高经济价值为 197.6190 万元。exitflag = 1 表示过程正常收敛于解 x 处。

2.工作人员计划安排问题

• •  某昼夜服务的公共交通系统每天各时间段(每 4 小时为一个时间段)所需的值班人数如表所示，这些值班人员在某一时段开始上班后要连续工作 8 小时(包括轮流用餐时间)，请问该公共交通系统至少需要多少名工作人员才能满足值班的需要？

• • 这里可设 $x_i$ 为第 i 个时段开始上班的人员数

    clc
    clear
    f = [1;1;1;1;1;1];
    A = [-1 0 0 0 0 -1
         -1 -1 0 0 0 0
         0 -1 -1 0 0 0
         0 0 -1 -1 0 0
         0 0 0 -1 -1 0
         0 0 0 0 -1 -1];
    b = [-50;-30;-70;-60;-40;-20];
    lb = zeros(6,1);    

  • 然后调用 linprog 函数

    [x,fval,exitflag,output,lambda] = linprog(f,A,b,[],[],lb)

  • 最优化结果如下：

 　　　　　　可见只要 6 个时段分别安排 26 人、25 人、45 人、26 人、14 人和 24 人就可以满足值班的需要，共计 160 人，并且计算结果 exitflag = 1 是收敛的

 3. 投资问题

• • 某单位有一批资金用于 4 个工程项目的投资，用于各工程项目时所得的净收益(投入资金的百分比)如表所示

• • 由于某种原因，决定用于项目 A 的投资不大于其他各投资之和，而用于项目 B 和 C 的投资要大于项目 D 的投资，试确定使该单位收益最大的投资分配方案。
  • 这里可以用 $x_1、x_2、x_3 和 x_4$ 分别代表用于项目 A、B、C 和 D 的投资百分数，由于各项目的投资百分数之和必须等于 100%，所以 $x_1+x_2+x_3+x_4 = 1$，代码设置如下：

    f = [-0.18;-0.1;-0.09;-0.12];
    A = [1 -1 -1 -1
         0 -1 -1 1];
    b = [0;0];
    Aeq = [1 1 1 1];
    beq = [1];
    lb = zeros(4,1); 

  • 调用函数：

    [x,fval,exitflag,output,lambda] = linprog(f,A,b,Aeq,beq,lb)

  • 结果如下：

说明 A、B、C、D 投入资金的百分比分别为 50%、25%、0%、25% 时，该单位收益最大

4. 工件加工任务分配问题

• •  某车间有两台机床甲和乙，可用于加工 3 种工件。假定这两台机床的可用台时数分别为 600 和 900,3 种工件的数量分别为 400、600 和 500，且已知用两台不同机床加工单位数量的不同工件所需的台时数和加工费用(如表所示)，问怎样分配机床的加工任务，才能既满足加工工件的需求，又使总加工费用最低？

• • 这里可设在甲机床上加工工件1、2 和 3 的数量分别为 $x_1、x_2、x_3$，在乙机床上加工工件1、2 和 3 的数量分别为 $x_4、x_5、x_6$，根据 3 种工种的数量限制，则有：$x_1+x_4 = 400(对工件 1) ，x_2+x_5 = 600(对工件 2)，x_3+x_6=500(对工件 3)$，根据题意：

    clc
    clear
    f = [13;9;10;11;12;8];
    A = [0.6 1.2 1.1 0 0 0
         0 0 0 0.4 1.2 1.0];
    b = [600;900];
    Aeq = [1 0 0 1 0 0
           0 1 0 0 1 0
           0 0 1 0 0 1];
    beq = [400 600 500];
    lb = zeros(6,1);

    然后调用 linprog 函数：

    [x,fval,exitflag,output,lambda] = linprog(f,A,b,Aeq,beq,lb)

    结果如下：

在甲机床上加工 500 个工件 2，在乙机床上加工 400 个工件 1、加工 100 个工件 2、加工 500 个工件 3，可在满足条件的情况下使总加工费用最小，最小费用为 14100 元。

 5. 厂址选择问题

• •  A、B、C 三地，每地都出产一定数量的产品，也消耗一定数量的原料(如表所示)，已知制成每吨产品需 3 吨原料，各地之间的距离为：A-B，150km；A-C，100km，B-C，200km。假定每万吨原料运输 1lm 的运价是 5000 元，每万吨产品运输 1lm 的运价是 6000 元。由于地区条件的差异，在不同地点设厂的生产费用也不同。问究竟在哪些地方设厂，规模多大，才能使总费用最小？另外，由于其他条件限制，在 B 处建厂的规模(生产的产品数量)不能超过 6 万吨

• • 这里可令 $x_{ij}$ 为由 i 地运到 j 地的原料数量(万吨)，$y_{ij}$ 为由 i 地运往 j 地的产品数量(万吨)，i，j = 1,2,3(分别对应A、B、C三地)，根据题意：

    clc
    clear
    f = [75;75;50;50;100;100;150;240;210;120;160;220];
    A = [1 -1 1 -1 0 0 3 3 0 0 0 0
         -1 1 0 0 1 -1 0 0 3 3 0 0
         0 0 -1 1 -1 1 0 0 0 0 3 3
         0 0 0 0 0 0 0 0 1 1 0 0];
    b = [21;17;22;6];
    Aeq = [0 0 0 0 0 0 1 0 1 0 1 0
                0 0 0 0 0 0 0 1 0 1 0 1];
    beq = [6;12];
    lb = zeros(12,1);
    [x,fval,exitflag,output,lambda] = linprog(f,A,b,Aeq,beq,lb);

    

    可见要使总费用最小，A、B、C 三地的建厂规模分别为 6 万吨、5.667 万吨和 6.333 万吨，最小总费用为 2.9733e+03 万元

 6. 确定职工编制问题

• • 某工厂每日 8小时的产量不低于 1800 件。为了进行质量控制，计划聘请两个不同水平的检验员。一级检验员的速度为 25件/小时，正确率 98%，计时工资 4元/小时，二级检验员的速度为 15件/小时，正确率 95%，计时工资 3元/小时，检验员每错一次，工厂要损失 2 元。现有可供厂方聘请的检验员人数为一级 7人和二级 8人。为使总检验费用最省，该工厂应聘请一级、二级检验员各多少名？
  • 可设需要一级和二级检验员的人数分别为 $x_1$ 和 $x_2$ 名，根据题意：

    clc
    clear
    f = [40;36];
    A = [1 0
         0 1
         -5 -3];
    b = [7;8;-45];
    lb = zeros(2,1);
    [x,fval,exitflag,output,lambda] = linprog(f,A,b,[],[],lb);

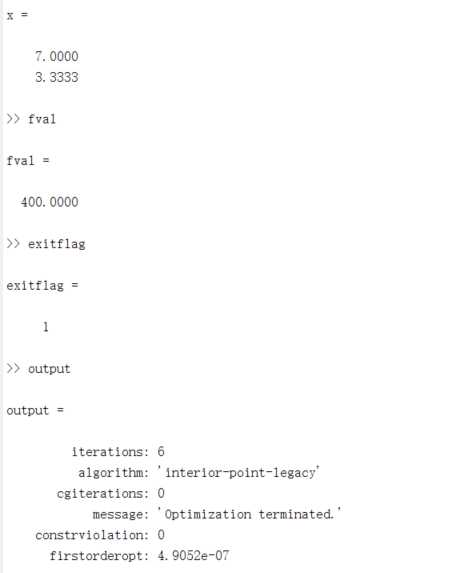
可见，招聘一级检验员 7名，二级检验员 3名可使总检验费用最少，约为400.00元

7. 生产计划的最优化问题

• • 某工厂生产 A 和 B 两种产品，它们需要经过 3 种设备的加工，其加工如表所示，设备一、二和三每天可使用的时间分别不超过 11、9 和 12小时。产品 A 和 B 的利润随市场的需求有所波动，如果预测未来某个时期内 A 和 B 的利润分别为 5000元/吨和 3000元/吨，问在那个时期内，每天应生产A、B各多少吨，才能使工厂获利最大?

• • 这里可设每天应安排生产 A 和 B 分别为 $x_1$ 和 $x_2$ 吨，根据题意：

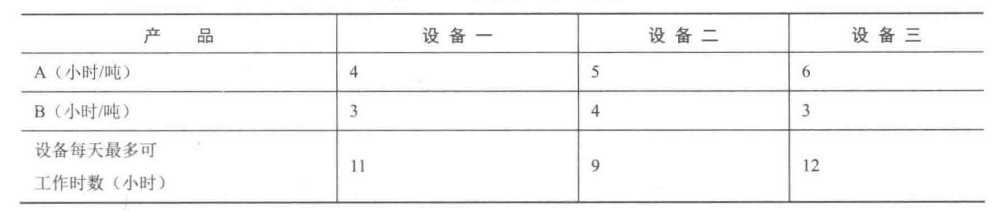
    clc
    clear
    f = [-5;-3];
    A = [4 3
         5 4
         6 3];
    b = [11;9;12];
    lb = zeros(2,1);
    [x,fval,exitflag,output,lambda] = linprog(f,A,b,[],[],lb)

    

    每天生产 A 产品 1.80吨、B产品 0 吨可使工厂获得最大利益 9000元/吨。

MATLAB 线性规划实例应用

标签：选择   开始   招聘   分析   没有   分配   生产   lag   系统   

原文地址：https://www.cnblogs.com/NikkiNikita/p/9464886.html