标签:init 延伸 lld define mat 否则 max || oid
?这题好神仙啊qwq疯狂orz看懂日文题解的sjk太强啦qwq
? ?
? ?首先我们要统计的东西,是一个涂黑的连通块,然后我们考虑找一个东西使得它可以和每个不同的连通块(也就是不同的染色方案)一一对应,那么这里我们找这个连通块的直径的中心部分(以下简称中心),这个中心根据直径的长度为奇数或者偶数可以是一个点或者一条边
?那么现在,如果说我们知道了中心(一个点或者一条边),知道了半径(就是直径的一半),这个连通块就确定下来了
? ?那么现在我们要做的就是枚举中心,然后看以其为中心能有多少种不同的半径选择,一种选择方案合法当且仅当存在一个点\(x\)和一个非负整数\(d\)能够将其构造出来
?
? ?那么接下来我们就可以愉快分类讨论了
? ?为了方便下面的描述,我们先统一一些记号:
\(depmx[x]\):以\(x\)的子树的最大深度(关于这个子树到底是哪种,依下面的描述定)
\(dis(x,y)\):\(x\)到\(y\)在树上的简单路径长度
?
? ?先看比较简单的情况:中心是一条边\((u,v)\)

? ?我们用三角形直观地表示其“子树”,三角形的大小反映的是\(depmx[u]\)和\(depmx[v]\)的大小关系,那么这条边为中心的贡献是:如果\(u\)中(\(depmx\)较小的那个点)有可选的点,那么对答案有\(1\)的贡献,否则没有贡献
? ?具体是因为,我们要保证存在一个\(x\)和\(d\)能够构造这种方案,那么假设\(u\)中有可选的点,我们如果要构造出这个连通块并且保证\((u,v)\)是中心的话,\(u\)的整个“子树”中的所有点必须涂完,否则无法涂到\(v\)的子树中对应的位置,\((u,v)\)就不是中心了
? ?而如果说\(u\)中没有可选的点,考虑选择\(v\)中的一个点来构造,会发现这是不行的,因为两边必定不对称,无法保证\((u,v)\)是中心
? ?
? ?接下来是稍微复杂一点的情况:中心是一个点\(u\)
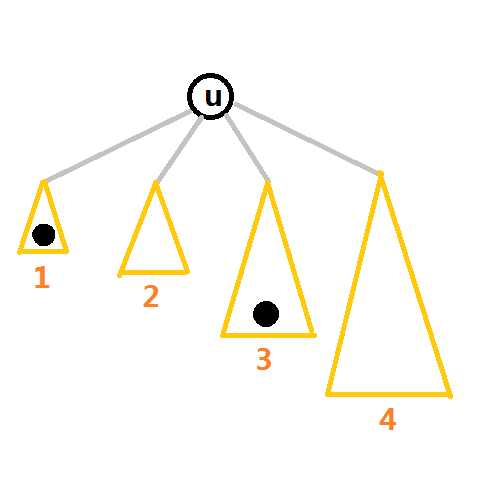
? ?同样的我们还是直观地用三角形表示子树,然后用三角形的。。高度来表示\(depmx\)之间的相对大小,有黑点表示这个子树中有可选的点,没有反之,为了方便下面的表述,我们给子树编号为\(1,2,3,4\)
? ?感性理解一下。。半径的可选范围应该是一段区间,那么现在我们要做的就是卡出上界和下界
? ?这里我们还需要分两个小类讨论
(1)\(u\)是一个可选点
? ?如果\(u\)可选,那么下界显然就是\(0\)(只涂自己一个点),上界的话就是所有后继子树中(也就是上图中的\(1,2,3,4\)号子树)\(depmx\)的次大值
? ?为什么不能是最大值呢?因为一旦半径是最大值,显然\(4\)号子树会被涂完,\(1\sim 3\)号子树也会被涂完,但是这个时候直径的中点就不是我们钦定的中心\(u\)了,只有在\(depmx\)次大值之前,我们可以保持这样一个状态:
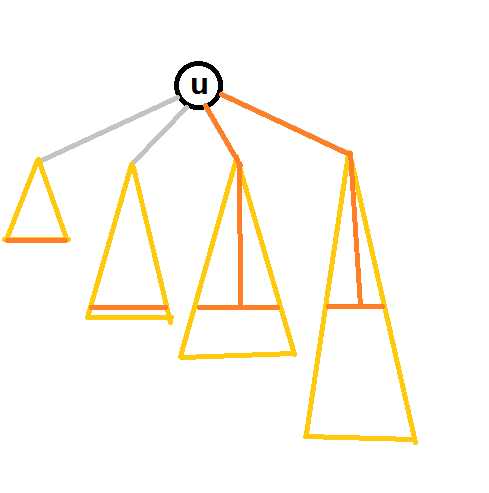
? ?橙色线以上是涂色涂到的部分,过\(u\)的橙色线是直径,只要半径的长度是\(<=depmx\)次大值的,我们一定可以将直径的两个端点定在次深子树的“边界”和最深子树的“边界”上,这样一定能保证\(u\)是中心,而如果\(>depmx\)次大值了,中心就会向最深子树那个方向偏移
?所以这部分的贡献是:\(depmx\)次大值+1
?
(2)\(u\)不是一个可选点
? ?如果\(u\)不可选,那么显然下界是需要调整的
? ?下界应该调整为有可选点的子树中\(depmx\)的最小值,因为为了涂到\(u\)并且保证\(u\)为直径的中点,最小的那个子树必须涂完(具体可以考虑,假设一个我们选择的\(x\)在这个最小的子树内,那么\(x\)自然要先涂到\(u\),这样\(x\)以下的节点也会被涂到,然后为了保证\(u\)是中心,这个半径的长度还需要继续扩大,对应的\(x\)下更深的节点也会继续被涂到,这样一直延伸直到\(x\)所在的整个子树都被涂完,\(x\)在其他子树中的情况类似)
? ?接着就是上界,我们是否可以继续使用(1)中的结论呢?
? ?答案是肯定的,同样我们也可以考虑,假设\(x\)在次深子树中,同样延伸的话最后会将次深子树涂完,然后我们可以得到一条类似(1)中所说的那样的直径,\(x\)在其他子树中类似
? ?所以这部分的贡献是:有可选点的子树的\(depmx\)的最小值-\(depmx\)次小值+1
? ?
? ?注意,如果说没有后继儿子,这个点的贡献就是:如果这个点是可选点,贡献为\(1\),否则贡献为\(0\)
?
? ?然后我们就可以快乐树d在\(O(n)\)内预处理出往下的\(depmx\)和往上的\(depmx\)然后就可以快乐求解啦
?
? ?代码大概长这个样子
#include<iostream>
#include<cstring>
#include<cstdio>
#define ll long long
using namespace std;
const int N=2*(1e5)+10,inf=2147483647;
struct xxx{
int y,nxt,x;
}a[N*2];
struct Data{/*{{{*/
int mx,smx,idmx;
void init(){mx=-1; smx=-1; idmx=-1;}
void update(int delta,int id1){
if (mx<delta)
smx=mx,mx=delta,idmx=id1;
else
smx=max(smx,delta);
}
}info[N];/*}}}*/
char s[N];
int h[N],depmx[N][2],ok[N],cnt[N][2],dep[N];
int n,m,tot,all;
ll ans;
void add(int x,int y){a[++tot].y=y; a[tot].nxt=h[x]; h[x]=tot; a[tot].x=x;}
void dfs(int fa,int x,int d){
int u;
dep[x]=d;
depmx[x][0]=depmx[x][1]=0;
info[x].init();
info[x].update(0,x);
cnt[x][0]=cnt[x][1]=ok[x];
for (int i=h[x];i!=-1;i=a[i].nxt){
u=a[i].y;
if (u==fa) continue;
dfs(x,u,d+1);
depmx[x][0]=max(depmx[x][0],depmx[u][0]+1);
info[x].update(depmx[u][0]+1,u);
cnt[x][0]+=cnt[u][0];
}
}
void dfs1(int fa,int x){
int u;
if (fa){
if (x==info[fa].idmx){
if (info[fa].smx!=-1){
depmx[x][1]=max(depmx[x][1],info[fa].smx+1);
info[x].update(info[fa].smx+1,fa);
}
}
else{
if (info[fa].mx!=-1){
depmx[x][1]=max(depmx[x][1],info[fa].mx+1);
info[x].update(info[fa].mx+1,fa);
}
}
cnt[x][1]=cnt[fa][1]+cnt[fa][0]-cnt[x][0];
}
for (int i=h[x];i!=-1;i=a[i].nxt){
u=a[i].y;
if (u==fa) continue;
dfs1(x,u);
}
}
int solve_edge(int i){
int x=a[i].x,y=a[i].y,tmp;
int depx,depy,cntx,cnty;
if (dep[x]>dep[y]) swap(x,y);
depy=depmx[y][0]; cnty=cnt[y][0];
cntx=all-cnty;
if (y==info[x].idmx) depx=info[x].smx;
else depx=info[x].mx;
if (depx==depy&&(cntx||cnty)) return 1;
if (depx<depy&&cntx==0) return 0;
if (depy<depx&&cnty==0) return 0;
return 1;
}
int solve_vertice(int x){
int son=0,u;
for (int i=h[x];i!=-1;i=a[i].nxt) ++son;
//son+=dep[a[i].y]<dep[x]?cnt[a[i].y][1]:cnt[a[i].y][0];
if (son<=1) return ok[x];
int up,dw=inf,smx=-1,mx=depmx[x][1];
if (depmx[x][1]>0&&all-cnt[x][0]) dw=min(dw,depmx[x][1]);
for (int i=h[x];i!=-1;i=a[i].nxt){
u=a[i].y;
if (dep[u]<dep[x]) continue;
if (cnt[u][0])
dw=min(dw,depmx[u][0]+1);
if (depmx[u][0]+1>mx)
smx=mx,mx=depmx[u][0]+1;
else
smx=max(smx,depmx[u][0]+1);
}
up=smx;
if (ok[x]) dw=0;
if (dw==inf) return 0;
if (up<dw) return 0;
return up-dw+1;
}
int main(){
#ifndef ONLINE_JUDGE
freopen("a.in","r",stdin);
#endif
int x,y;
scanf("%d",&n);
memset(h,-1,sizeof(h));
tot=0;
for (int i=1;i<n;++i){
scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
scanf("%s",s+1);
all=0;
for (int i=1;i<=n;++i) ok[i]=s[i]-'0',all+=ok[i];
dfs(0,1,1);
dfs1(0,1);
for (int i=1;i<=tot;i+=2)
ans+=solve_edge(i);
for (int i=1;i<=n;++i)
ans+=solve_vertice(i);
printf("%lld\n",ans);
}标签:init 延伸 lld define mat 否则 max || oid
原文地址:https://www.cnblogs.com/yoyoball/p/9483816.html