标签:url features ted boost 元素 素数 api 相似度 ima
人脸检测属于计算机视觉的范畴,早期人们的主要研究方向是人脸识别,即根据人脸来识别人物的身份,后来在复杂背景下的人脸检测需求越来越大,人脸检测也逐渐作为一个单独的研究方向发展起来。
目前人脸检测的方法主要有两大类:基于知识和基于统计。
基于知识的方法:主要利用先验知识将人脸看作器官特征的组合,根据眼睛、眉毛、嘴巴、鼻子等器官的特征以及相互之间的几何位置关系来检测人脸。主要包括模板匹配、人脸特征、形状与边缘、纹理特性、颜色特征等方法。
基于统计的方法:将人脸看作一个整体的模式——二维像素矩阵,从统计的观点通过大量人脸图像样本构造人脸模式空间,根据相似度量来判断人脸是否存在。主要包括主成分分析与特征脸、神经网络方法、支持向量机、隐马尔可夫模型、Adaboost算法等。
本文中介绍的Haar分类器方法,包含了Adaboost算法,稍候会对这一算法做详细介绍。所谓分类器,在这里就是指对人脸和非人脸进行分类的算法,在机器学习领域,很多算法都是对事物进行分类、聚类的过程。
我们要探讨的Haar分类器实际上是Boosting算法的一个应用,Haar分类器用到了Boosting算法中的AdaBoost算法,只是把AdaBoost算法训练出的强分类器进行了级联,并且在底层的特征提取中采用了高效率的矩形特征和积分图方法,这里涉及到的几个名词接下来会具体讨论。
在2001年,Viola和Jones两位大牛发表了经典的《Rapid Object Detection using a Boosted Cascade of Simple Features》和《Robust Real-Time Face Detection》,在AdaBoost算法的基础上,使用Haar-like小波特征和积分图方法进行人脸检测,他俩不是最早使用提出小波特征的,但是他们设计了针对人脸检测更有效的特征,并对AdaBoost训练出的强分类器进行级联。这可以说是人脸检测史上里程碑式的一笔了,也因此当时提出的这个算法被称为Viola-Jones检测器。又过了一段时间,Rainer Lienhart和Jochen Maydt两位大牛将这个检测器进行了扩展,最终形成了OpenCV现在的Haar分类器。
AdaBoost是Freund和Schapire在1995年提出的算法,是对传统Boosting算法的一大提升。Boosting算法的核心思想,是将弱学习方法提升成强学习算法,也就是“三个臭皮匠顶一个诸葛亮”。
Haar分类器 = Haar-like特征 + 积分图方法 + AdaBoost +级联;
Haar分类器算法的要点如下:
Haar(哈尔)特征分为三类:边缘特征、线性特征、中心特征和对角线特征,组合成特征模板。特征模板内有白色和黑色两种矩形,并定义该模板的特征值为白色矩形像素和减去黑色矩形像素和。Haar特征值反映了图像的灰度变化情况。例如:脸部的一些特征能由矩形特征简单的描述,如:眼睛要比脸颊颜色要深,鼻梁两侧比鼻梁颜色要深,嘴巴比周围颜色要深等。但矩形特征只对一些简单的图形结构,如边缘、线段较敏感,所以只能描述特定走向(水平、垂直、对角)的结构。

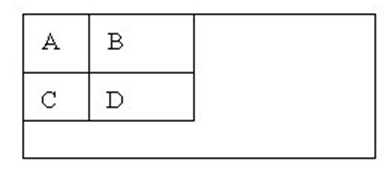
对于图中的A, B和D这类特征,特征数值计算公式为:v=Σ白-Σ黑,而对于C来说,计算公式如下:v=Σ白-2*Σ黑;之所以将黑色区域像素和乘以2,是为了使两种矩形区域中像素数目一致。我们希望当把矩形放到人脸区域计算出来的特征值和放到非人脸区域计算出来的特征值差别越大越好,这样就可以用来区分人脸和非人脸。
通过改变特征模板的大小和位置,可在图像子窗口中穷举出大量的特征。上图的特征模板称为“特征原型”;特征原型在图像子窗口中扩展(平移伸缩)得到的特征称为“矩形特征”;矩形特征的值称为“特征值”。

上图中两个矩形特征,表示出人脸的某些特征。比如中间一幅表示眼睛区域的颜色比脸颊区域的颜色深,右边一幅表示鼻梁两侧比鼻梁的颜色要深。同样,其他目标,如眼睛等,也可以用一些矩形特征来表示。使用特征比单纯地使用像素点具有很大的优越性,并且速度更快。
矩形特征可位于图像任意位置,大小也可以任意改变,所以矩形特征值是矩形模版类别、矩形位置和矩形大小这三个因素的函数。故类别、大小和位置的变化,使得很小的检测窗口含有非常多的矩形特征,如:在24*24像素大小的检测窗口内矩形特征数量可以达到16万个。这样就有两个问题需要解决了:(1)如何快速计算那么多的特征?---积分图大显神通;(2)哪些矩形特征才是对分类器分类最有效的?---如通过AdaBoost算法来训练。详情参考:集成学习值Adaboost算法原理和代码小结(转载)
积分图就是只遍历一次图像就可以求出图像中所有区域像素和的快速算法,大大的提高了图像特征值计算的效率。
积分图主要的思想是将图像从起点开始到各个点所形成的矩形区域像素之和作为一个数组的元素保存在内存中,当要计算某个区域的像素和时可以直接索引数组的元素,不用重新计算这个区域的像素和,从而加快了计算(这有个相应的称呼,叫做动态规划算法)。积分图能够在多种尺度下,使用相同的时间(常数时间)来计算不同的特征,因此大大提高了检测速度。
积分图是一种能够描述全局信息的矩阵表示方法。积分图的构造方式是位置$(i,j)$处的值$ii(i,j)$是原图像$(i,j)$左上角方向所有像素$f(k,l)$的和:$$ii(i,j)=\sum\limits_{k≤i,l≤j}f(k,l)$$
积分图构建算法:
1、用$s(i,j)$表示行方向的累加和,初始化$s(i,-1)=0$;
2、使用$ii(i,j)$表示一个积分图像,初始化$ii(-1,i)$=0;
3、逐行扫描图像,递归计算每个像素$(i,j)$行方向的累加和$s(i,j)$和积分图像$ii(i,j)$的值:
$$s(i,j)=s(i,j-1)+f(i,j)$$
$$ii(i,j)=ii(i-1,j)+s(i,j)$$
4、扫描图像一遍,当到达图像右下角像素时,积分图像$ii$就构建好了。
积分图构造好之后,图像中任何矩阵区域像素累加和都可以通过简单运算得到如图所示:
设D的四个顶点分别为α,β,γ,δ则D的像素和可以表示位$$D_{sum}=ii(α)+ii(β)-(ii(γ)+ii(δ))$$
而Haar-like特征值无非就是两个矩阵像素和的差,同样可以在常数时间内完成。
标签:url features ted boost 元素 素数 api 相似度 ima
原文地址:https://www.cnblogs.com/zyly/p/9410563.html