标签:欧拉定理 特殊情况 for i++ 图片 const .com 范围 names
假如p是质数,且gcd(a,p)=1,那么 a^(p-1)≡1(mod p)
也就是a^(p-1) %p=1
据说它是欧拉定理的一种特殊情况,也就是
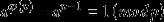
比较神奇,据说很出名很出名很出名
先回顾一下乘法逆元
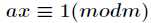
x的最小整数解称为a模m的逆元
如果这个m是个质数,那么费马小定理就派上用场喽
这个时候x的最小整数解是
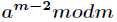
推导过程:
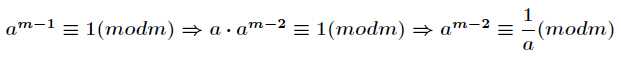
只可意会不可言传的样子。
例题是HDU4704,题意是:求1-n中,组成n的不同种数
用隔板法思考,在n个1里面插隔板有几种插法
结果是2^(n-1)
然后呢?就是计算它了,质数的范围是1e6,那么好,按题意取模
也就是求2^(n-1)%mod
费马小定理a^b%c=a^(b%(c-1))%c
使用的前提是mod是个质数
对于任意自然数,当要求a^p%m时,就可以利用费马小定理化简,只需求(a^(p%(m-1)))%m(p是素数)
记住这句话,题目就很显然了
我们将n拆成多个 a*(p-1) + k ,也就是2^n = 2^[a*(p-1) + k ] % mod = 2^k % mod
在这里p直接等于mod,就那么中括号的左半部分因为费马小定理就化没了,只剩下个k
要求的是2^(n-1),计算出k后,减一直接快速幂即可
1 #include<cstdio> 2 #include<cstring> 3 using namespace std; 4 const long long MOD=1000000007; 5 char s[1000005]; 6 long long cal(long long m) 7 { 8 int len=strlen(s); 9 long long ans=0; 10 for(int i=0;i<len;i++) 11 ans=(ans*10+s[i]-‘0‘)%m; 12 return ans; 13 } 14 long long pow_mod(long long a,long long b) 15 { 16 long long ans=1; 17 while(b!=0) 18 { 19 if(b&1) ans=ans*a%MOD; 20 a=a*a%MOD; 21 b>>=1; 22 } 23 return ans; 24 } 25 int main() 26 { 27 while(scanf("%s",s)==1) 28 { 29 long long k=cal(MOD-1); 30 printf("%lld\n",pow_mod(2,k-1)); 31 } 32 return 0; 33 }
标签:欧拉定理 特殊情况 for i++ 图片 const .com 范围 names
原文地址:https://www.cnblogs.com/aininot260/p/9484148.html