标签：遇到   text   假设   mat   span   bzoj   复杂度   alt   ota   

启发式合并

• 刚听到这个东西的时候，我是相当蒙圈的。特别是“启发式”这三个字莫名的装逼，因此之前一直没有学。
• 实际上，这个东西就是一个SB贪心。
• 以堆为例，若我们要合并两个堆a、b，我们有一种极其简单的做法：那就是比较一下它们的大小，将小的堆的每个元素依次插入到大的堆中。不妨设\(|a|≤|b|\)，则时间复杂度即为：\(O(|a|*log_2(|a|+|b|))\)。
• 这个东西看似很慢，但当点数较小的时候，我们可以证明复杂度是可被接受的。

• 比如我们要合并n个堆，这n个堆共有m个点。设这n个堆\(=\{s_1,s_2,s_3,...,s_n\}\)。
• 首先，我们合并\(s_1\)和\(s_2\)，变成一个新的堆\(t_1\)。
• 然后，我们合并\(t_1\)和\(s_3\)，变成一个新的堆\(t_2\)。
• ……
• 以此类推，我们最终可以合并出一个堆\(t_{n-1}\)。

• 合并堆a、b时，记1次操作为将a中的一个元素插入b（或将b中的一个元素插入a）。
• 可以发现，第1次合并操作数\(≤|s_2|\)，第2次合并操作数\(≤|s_3|\)……第i次合并操作数\(≤|s_{i+1}|\)。
• 因此，总操作数\(≤\sum_{i=2}^n|s_i|≤m\)。而每次操作又是\(O(log_2m)\)的复杂度。因此：

• 时间复杂度：\(O(n+mlog_2m)\)。

  推广

• 启发式合并也可以用到set、splay、treap等平衡树上去。
• 若我们要合并两棵平衡树a、b，也是先比较大小，将小的平衡树的每个元素依次插入大的平衡树。囿于插入的时间也是\(O(log_2n)\)，因此总复杂度还是\(O(|a|*log_2(|a|+|b|))\)。

• 注意：这里的合并并非treap的merge。merge(a,b)是强行让a所有元素的键值（要满足二叉排序树的性质的那个值）均小于b所有元素的键值，所以可以\(O(log_2n)\)做到；而这里要合并的两棵平衡树a、b的键值可能是交错不齐的。

  线段树合并

• OI中常常遇到一些题目，要将若干物件不断合并，维护信息。
• 如果合并的顺序不对，堆/平衡树的启发式合并会很慢。比如当你分治+启发式合并的时候，时间复杂度就变成\(O(n*(log_2n)^2)\)了。

• 这个时候，就需要线段树合并。

• 对于这个，相信大家都想得出下面这种合并步骤：
  
• 为了方便确定一棵树是否为空，我们动态开点。
• 比如，我们合并两棵权值线段树：
  
• 显然，这么做的复杂度与两棵树公共的节点数成正比。
• 但是，假设我们要合并多棵线段树呢？

• 假设我们要合并n棵线段树，定义势能函数\(\Phi(n)\)为它们的节点个数和。
• 每次合并线段树a、b时，设其公共点数为c，则合并后的\(\Phi(n)\)减少c，而时间复杂度增加c。
• 因此，时间复杂度应≤节点个数和。
• 当线段树中总共有m个元素时（比如n棵权值线段树，只存有m个数），每个元素都可以动态开辟至多\(log_2n\)个节点。因此，此时的时间复杂度应为\(O(n+mlog_2n)\)。

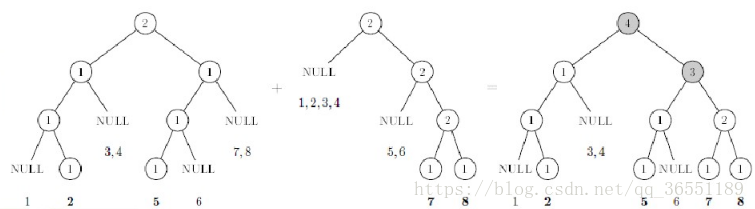
• 注意：此时的时间复杂度并不受合并顺序的限制。换句话说，不论你按什么顺序合并，只要你是合并n棵只有m个元素的线段树，时间复杂度就是\(O(n+mlog_2n)\)。

  例题

  【BZOJ 2212】【Poi2011】 Tree Rotations
  【JZOJ5800】【洛谷P4416】 [COCI2017-2018#1] 被单

启发式合并（堆、set、splay、treap）/线段树合并学习小记

标签：遇到   text   假设   mat   span   bzoj   复杂度   alt   ota   

原文地址：https://www.cnblogs.com/Iking123/p/9484432.html