标签:lld algo img nbsp 部分 namespace bubuko \n return
若n,a为正整数,且n,a互质,(a,n) = 1,则a^φ(n) ≡ 1 (mod n)
特别的φ(1)=1
费马小定理是欧拉定理的一种特殊情况
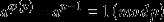
之前介绍的费马小定理是用来化简幂取模运算的,欧拉定理同样可以做到:
a^x≡a^(x%φ(m))(mod m)
这样就可以了
之前的费马小定理是让指数部分模一个p-1
然后这里是让指数部分模一个欧拉函数φ(m)其实一个意思
看一道例题,HDU1395
2^x mod n = 1,或者写成 2^x ≡ 1 (mod n)
求x
然后发现n为偶数或者是n为0时无解,答案必定是一个奇数
然后根据欧拉定理:
欧拉定理:a^(euler_phi(n))≡1(mod n),(a,n互质)
其中euler_phi为欧拉函数,计算不超过n且与n互质的个数
求法是n*∏(pi-1)/pi,pi为n的质因子
这里可以表示为:m=euler_phi(n)
所以a^m%mod=1
不过m不一定是最小循环节,但m是一个循环节,则最小循环节必定是m的一个因子
因而找出所有m的因子,暴力搜索下就好了
其实这个的重点是求欧拉函数,欧拉函数也是有类似于埃式筛法的计算方法的
1 //2^x mod n = 1 2 #include<cstdio> 3 #include<cmath> 4 #include<algorithm> 5 using namespace std; 6 long long t,mod; 7 long long e[1005]; 8 long long euler_phi(long long n) 9 { 10 long long m=sqrt(n+0.5); 11 long long ans=n; 12 for(int i=2;i<=m;i++) 13 { 14 if(n%i==0) 15 { 16 ans=ans/i*(i-1); 17 while(n%i==0) n=n/i; 18 } 19 } 20 if(n>1) ans=ans/n*(n-1); 21 return ans; 22 } 23 void find(long long n) 24 { 25 e[t++]=n; 26 for(int i=2;i*i<=n;i++) 27 { 28 if(n%i==0) 29 { 30 if(i*i==n) e[t++]=i; 31 else 32 { 33 e[t++]=i; 34 e[t++]=n/i; 35 } 36 } 37 } 38 } 39 long long pows(long long a,long long b) 40 { 41 long long s=1; 42 while(b!=0) 43 { 44 if(b&1) s=(s*a)%mod; 45 a=(a*a)%mod; 46 b=b>>1; 47 } 48 return s; 49 } 50 int main() 51 { 52 long long n; 53 while(scanf("%lld",&n)==1) 54 if(n%2==0||n==1) 55 printf("2^? mod %d = 1\n",n); 56 else 57 { 58 long long m,ans; 59 m=euler_phi(n); 60 t=0; 61 find(m); 62 sort(e,e+t); 63 mod=n; 64 for(int i=0;i<t;i++) 65 { 66 if(pows(2,e[i])==1) 67 { 68 ans=e[i]; 69 break; 70 } 71 } 72 printf("2^%d mod %d = 1\n",ans,n); 73 } 74 return 0; 75 }
再回过头来对比一下欧拉定理和费马小定理
费马小定理要求模数p必须是个质数,且a和p互质:a^(p-1) ≡1(mod p)
欧拉定理只要求a和m互质即可:a^φ(m)≡1(mod m)
标签:lld algo img nbsp 部分 namespace bubuko \n return
原文地址:https://www.cnblogs.com/aininot260/p/9486160.html