满二叉树的循环递归

标签：title   ddr   其它   计算   时间   编号   奇数   12px   com   

1. 在二叉树的第n层上最多有2 ^n-1个节点 。（n>=1）
2. 二叉树中如果深度为d(有k层),那么最多有2^d-1个节点。(d>=1）
3. 二叉树按照从上到下从左到右依次编号，则若某节点编号为k，则其左右子树根节点编号分别为2k和2k+1;
4. 二叉树分类：满二叉树，完全二叉树

• 满二叉树：高度为h，由2^h-1个节点构成，除叶子结点外的所有结点均有两个子结点。节点数达到最大值。所有叶子结点必须在同一层上。

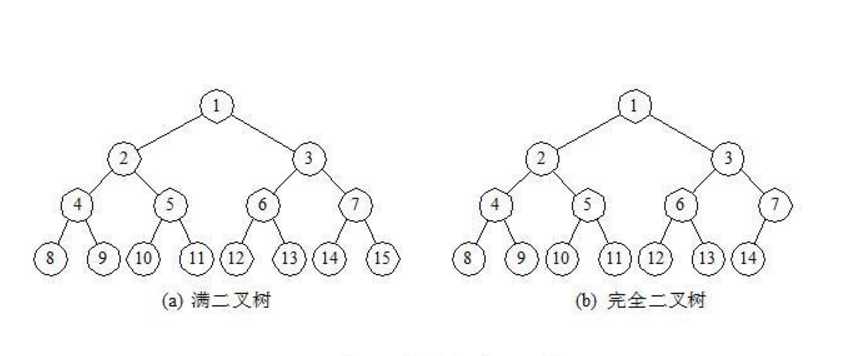
• 完全二叉树：
  若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

           1                                1
        /     \                          /          2        3                        2         3
   /    \    /    \                  /     \         4    5    6                     4         5         6
    完全二叉树                            不完全二叉树

在完全二叉树中，具有n个节点的完全二叉树的深度为[log₂n]+1，其中[log₂n]+1是向下取整。满二叉树的深度为d=log₂(n+1);

2.1 例题：
有一颗满二叉树，每个节点是一个开关，初始全是关闭的，小球从顶点落下，
小球每次经过开关就会把它的状态置反，这个开关为关时，小球左跑，为开时右跑。现在问第k个球下落到d层时的开关编号。输入深度d和小球个数k

思路分析：首先该题最先想到的是模拟，开一个数组表示开关，下标表示编号，根据k的子树为2k和2k+1来改变数组，判断进行。但是这样太麻烦了。而且根据深度和小球个数，导致计算量太大。
寻找规律:

1. 可以知道每一层，第奇数个落入该层的球都是往左，第偶数个落入该层的球都是往右。
2. 小球按照编号依次下落的，对于左枝（也就是奇数球)，每个I号小球落入该层都是第(k+1)/2个小球。而偶数是往右走的k/2个小球
3. 所以采取每一次一个循环，来判断k%2小球往哪儿走，循环d层，即可找出最后叶子！省去大数组和大时间

#include<stdio.h>

int res_arr[];

void find_addr(int k, int floor)
{
    int addr;
    addr = 1;
    res_arr[0] = addr;
    for(i = 1; i < floor; i++)
    {
        if(k%2)
        {
            k = (k+1)/2;
            addr = 2*addr;
            res_arr[i] = addr;
        }else
        {
            k = k/2;
            addr = 2*addr + 1;
            res_arr[i] = addr;
        }
    }
}

void main()
{
    int  i, f, k;
    printf("输入小球数及层数：");
    scanf('%d%d",&k,&f);
    find_addr(k,f);
    printf("\n第%d个小球将会经过如下位置\n:",k);
    for(i=0; i<f; i++)
    {
        printf("第%d层，第%d个位置\n", i, res_arr[i]);
    }
}

满二叉树的循环递归

标签：title   ddr   其它   计算   时间   编号   奇数   12px   com   

原文地址：https://www.cnblogs.com/shiqi17/p/9482180.html