标签:ret closed 分享图片 重复 factor src display printf http
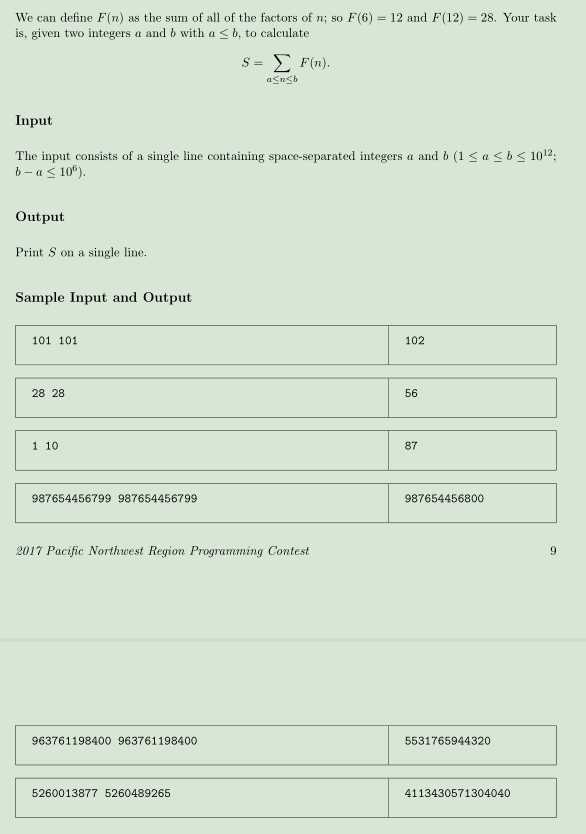
题意就是标题。
思路:
对于每个数 a 算出 1~a 的所有因数和sum(a),输出sum(b)-sum(a-1)。
关键在于如何求出 sum。
首先发现因数∈ 1 ≤ i ≤ n ,每个因数在区间[1,n]内的出现次数(不考虑4=2*2这样因数重复出现,这种情况2只算出现一次)等于 n/i (向下取整)。
然后用 t = n/(n/i) 可以找到与因数i出现次数相同的最大因数(这里可能有点难理解,例如1~100区间内21作为因数出现的数字有 21 ,42 ,63 ,84;即四次。按计算机整数相除默认向下取整规则可以知道 t = 25,手算一下就出来了,25作为因子在区间内出现的数字有 25 ,50 ,75 ,100;也是四次,而且21~25 内的数组作为因子时在区间内出现的次数都为4次)
所以得到求和公式 sum += (t+i)(t+1-i)/2*(n/i);

1 #include <cstdio> 2 #include <cstring> 3 #include <cmath> 4 using namespace std; 5 typedef unsigned long long LL; 6 LL a,b; 7 LL func(LL n){ 8 if ( n == 0) return 0; 9 LL sum = 0; 10 LL t = 0; 11 for (LL i=1; i<=n; i=t+1) {//已经计算了出现次数相同的因子i~t,故i=t+1,这样也能满足不超时 12 t = n/(n/i); 13 //printf("#%lld %lld\n",i,t); 14 sum += (i+t)*(t+1-i)/2*(n/i); 15 //printf("&%lld\n",n/i); 16 } 17 return sum; 18 } 19 int main(){ 20 while (scanf("%lld%lld",&a,&b)==2) { 21 printf("%lld\n",func (b)-func(a-1)); 22 } 23 return 0; 24 }
2017-2018 ACM-ICPC Pacific Northwest Regional Contest (Div. 2) P-Fear Factoring 区间内数的所有因数的和
标签:ret closed 分享图片 重复 factor src display printf http
原文地址:https://www.cnblogs.com/llllrj/p/9490087.html