标签:class 括号 ons cin namespace code std 知识 col
1,交集(∩)
多个事件若需同时满足,则取交集
2,并集(∪)
满足任意一个事件即可,则取并集
3,容斥原理
即先容再斥,以集合为例,求集合并。
则可以先单独考虑每个集合,然后直接都加起来,这样的话集合间的交集就会被重复计数,所以就有了容斥原理来消除这个重复计数。
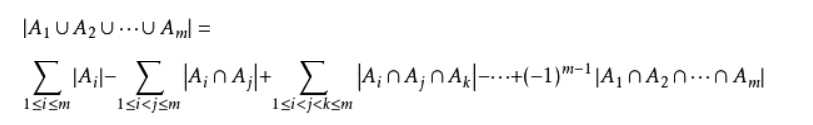
其实就是在将问题分成单个问题来考虑,原问题可以表示为单个问题的并集,且交集很好求,就能很愉快地使用容斥原理了。
德摩根定律:非(P 且 Q) = (非 P) 或 (非 Q),非(P 或 Q) = (非 P) 且 (非 Q)
有了这些知识就可以来分析杭电多校的一道题:

step1,当括号里的条件只为Xi>=0时,发现答案为C(k+m-1,m-1)
step2,再考虑有限制时,设集合Ai表示Xi超出限制,则原问题可以表示为非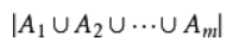
这就显然可以容斥定理了。
step3,Xi超出了限制,则它的取值范围为Xi >= n,那么给Xi减去n便使它的取值范围又回到了step1,再结合下德摩根定律便能得到答案了。
代码:
#include<stdio.h> #include<algorithm> #include<string.h> #include<map> #include<queue> #include<set> #include<iostream> #include<vector> #define MAXN 1000005 using namespace std; typedef long long ll; const ll mod = 998244353; ll fact[200005], ifact[200005], inv[200005]; void init() { fact[0] = 1; for(int i=1;i<=200000;i++) fact[i] = fact[i-1] * i % mod; inv[1] = 1; for (int i = 2; i <= 200000; i++) inv[i] = (mod - mod / i) * inv[mod % i] % mod; ifact[0] = 1; for(int i=1;i<=200000;i++) ifact[i] = ifact[i-1] * inv[i] % mod; } ll C(ll a,ll b) { if(b>a||a<0||b<0) return 0; return (fact[a]*ifact[b]%mod)*ifact[a-b]%mod; } int main() { int T; init(); cin>>T; while(T--) { ll n,m,k; cin>>n>>m>>k; ll sum=0; for(ll i=0;i<=m;i++) { if(i%2==0) { sum=(sum+C(m,i)*C(k-i*n+m-1,k-i*n)%mod)%mod; } else sum=(sum-C(m,i)*C(k-i*n+m-1,k-i*n)%mod)%mod; } cout<<(sum+mod)%mod<<endl; } }
标签:class 括号 ons cin namespace code std 知识 col
原文地址:https://www.cnblogs.com/lnu161403214/p/9490857.html