标签:arp 条件 取绝对值 几何 排除 center 推理 向量 严格
概率论使能够我们能够提出不确定性的声明以及在不确定性存在的情况下进行推理。概率论最初的发展是为了分析事件发生的频率。有一类事件是可以重复的(比如投掷一枚硬币,观察硬币落到正面还是反面),当我们说一个结果发生的概率为p,则如果我们进行无数次的反复实验,有p的比例会导致这样的结果。而另一类事件是不能重复的,比如医生根据病人的症状判断病人有40%的概率患有流感,在这个例子中,概率用来表示一种信任度,1表示非常肯定病人患有流感,0表示非常肯定病人没有流感。前面的一种概率,直接与时间发生的频率相联系,称之为频率派概率(frequentist probability);而后者则涉及到确定性水平,叫做贝叶斯概率(Bayesian probability)。
一个事件的所有可能结果组成这个事件的样本空间,其中的每一种结果叫做样本点。如果对于每一个样本点,都有一个唯一的实数与之对应,则就产生了一个样本点到唯一实数之间的函数,我们称该函数为随机变量。通俗地讲,随机变量就是将随机事件的结果量化。比如同时投掷两枚骰子,观察两枚骰子的点数,则样本空间共有36个样本点组成\(\{(i,j)|i=1,2...,6; j=1,2,...,6\}\),这里可以构造多个随机变量,比如随机变量x用来计算两个骰子点数之和,则x={2,3,...,12},这里就将每一个实验结果和一个实数映射了起来;再比如投掷一枚硬币,可能出现正面和反面,我们将正面映射到1,反面映射到0,则x(正面)=1,x(反面)=0,所以有\(P({\rm x}=1)=0.5,P({\rm x} = 0)=0.5\)。所以,随机变量实质上是函数。随机变量中的每一个取值及取值的概率被称为概率分布。
随机变量可以是离散的,也可以是连续的。如果一个随机变量的全部可能取值,只有有限多个或可列无穷多个,则称它是离散型随机变量,比如上面的计算两个骰子点数之和。相反,如果随机变量的取值为连续的(如全部实数,一段区间),则称它为连续型随机变量。
离散型随机变量对应的常见分布有:
连续型随机变量对应的常见分布有:
我们通常用无格式字体 (plain typeface) 中的小写字母来表示随机变量本身,而用手写体中的小写字母来表示随机变量能够取到的值。例如,\(x_1\) 和 \(x_2\) 都是随机变量 x 可能的取值,对于向量值变量,我们会将随机变量写成 x,它的一个可能取值为 \(x\)。
离散型随机变量的概率分布可以用分布律来描述(或者称为概率质量函数,probability mass function, PMF )。我们通常用大写字母\(P\)来表示离散型随机变量的分布律,如\(P(\)x\()\)表示离散型随机变量x的分布律。
分布律将随机变量中的每个取值映射到该取值的概率。x = \(x\)的概率用\(P(\)x\(=x)\)来表示。有时我们会先定义一个随机变量x,然后使用符号~来说明它遵循的分布:x~\(P(\)x\()\)。
分布律可以作用于多个随机变量,这种多个随机变量的概率分布被称为联合概率分布(joint probability distribution),如\(P(\)x=\(x\), y\(=y)\)表示x=\(x\),y=\(y\)同时发生的概率,有时可以简写为\(P(x,y)\)。
如果P是一个随机变量的分布律,则要满足下面几个条件:
连续型随机变量的概率分布可以使用概率密度函数(probability density function, PDF)来描述。如果一个函数\(p\)是概率密度函数,则\(p\)需要满足以下几条性质:
下面用一个例子来解释上面的几条性质。
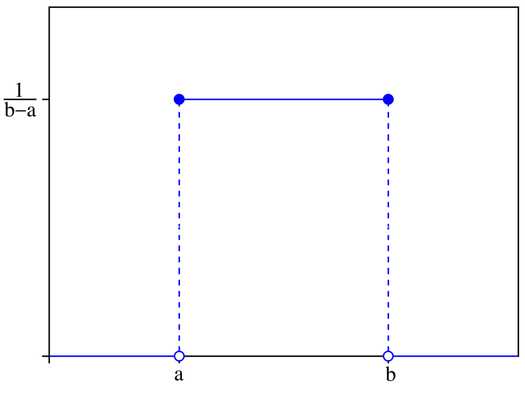
考虑在区间[a, b]上的均匀分布,我们用\(u(x;a,b)\)表示该分布的概率密度函数,\(x\)表示以\(x\)为参数,a,b是区间的端点且b>a,也就是\({\rm x}\)~\(u(x;a,b)\),则该均匀分布的概率密度曲线如下:
有时候,我们知道了一组变量的联合概率分布,但我们想了解某一个子集的概率分布,则这种定义在子集上的概率分布被称为边缘概率分布(marginal probability distribution)。
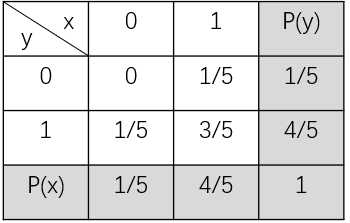
为什么叫边缘概率分布呢? 举个例子,假如有两个随机变量x, y的二维联合概率分布如下表:
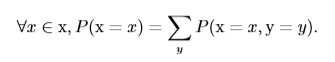
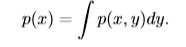
在很多情况下,我们感兴趣的是一个事件已经发生的情况下,另一个事件发生的概率,这种概率叫做条件概率。在事件x已经发生的情况下,事件y发生的概率表示为\(P({\rm y}=y|{\rm x}=x)\),可通过下面的公式计算:
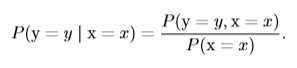
从上节的条件概率公式可以知道两个事件b,c同时发生的概率:\[P(b, c)=P(b|c)P(c)\],则三个事件a,b,c同时发生的概率为:\[P(a,b,c)=P(a|b,c)P(b,c)=P(a|b,c)P(b|c)P(c)\],由数学归纳法可以得到:
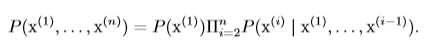
如果两个随机变量(事件)x,y同时发生的概率等于这两个变量(事件)单独发生的概率乘积,则称这两个随机变量是独立的,即:
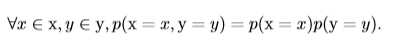
如果在随机变量(事件)z已经发生的情况下,随机变量(事件)x和y同时发生的概率等于x和y在z已发生的情况下分别发生的概率乘积,即:
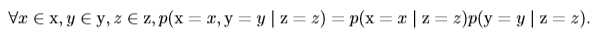
期望(expectation)就是随机变量取值的平均值。设\(f(x)\)是随机变量x的函数,则对于离散型随机变量x,f(x)的期望可以通过求和得到(比如我们知道x的分布,求\(f(x)=x^2\)的期望):
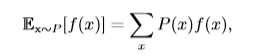
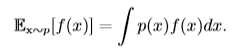
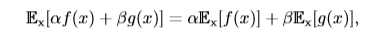
期望反映了随机变量分布的平均取值,但在实际问题中,我们不仅关心随机变量的平均取值,还关心随机变量的取值与平均取值(期望)的偏离程度,方差(variance)就是用来衡量这种偏离程度的,也就是衡量随机变量x取值的差异性。设f(x)是随机变量x的函数,则f(x)方差的计算公式如下:
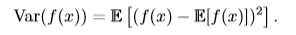
协方差(covariance)在某种意义上给出了两个随机变量之间的相关程度的大小。如随机变量x和y相互独立,则x与y的协方差Cov(x, y)=0。设f(x)是x的函数,g(y)是y的函数,则f(x)和g(y)的协方差计算方法为:
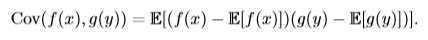
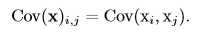
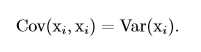
一般把只有两个对立结果的实验叫做伯努利实验,如投硬币就是一个伯努利实验,因为投掷的结果只有正面和反面。把伯努利实验在相同条件下重复进行n次,且这n次实验相互独立,则称这n次实验为n重(次)伯努利实验,或称为伯努利概型,对应的概率分布叫做二项分布。当n=1时,二项分布变为伯努利分布(又称两点分布,或者0-1分布),也就是说伯努利分布是只进行1次伯努利试验的概率分布。伯努利分布适用于离散型随机变量。
伯努利分布由单个参数Φ∈[0,1]控制,Φ给出了随机变量x等于1(如硬币正面)的概率,则P(x=0)=1-Φ。伯努利分布具有如下性质:
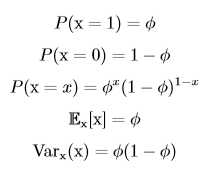
在10.1中介绍了二项分布,指在每次实验中,实验结果只有两个状态(投硬币)。若每次实验的实验结果有k个状态(投骰子),进行n次相互独立的实验对应的概率分布叫做多项式分布,或者范畴分布。多项式分布由向量\(p∈[0, 1]^{k-1}\)参数化,其中\(p_i\)表示第i个状态发生的概率,最后第k个状态的概率可以通过\(1-1^Tp\)求出。多项式分布适用于离散型随机变量。
伯努利分布和多项式分布足够用来描述在它们领域内的任意分布。它们能够描述这些分布,不是因为它们特别强大,而是因为它们的领域很简单;它们可以对那些能够将所有的状态进行枚举的离散型随机变量进行建模。当处理的是连续型随机变量时,会有不可数无限多的状态,所以任何通过少量参数描述的概率分布都必须在分布上加以严格的限制。
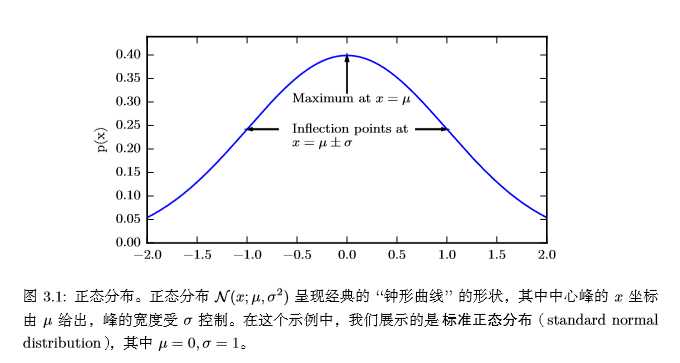
实数上最常用的分布就是正态分布(normal distribution),也称为高斯分布 (Gaussian distribution):
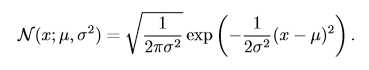
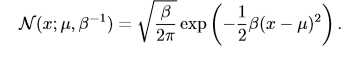
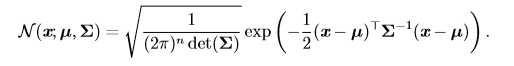
在深度学习中,我们经常会需要一个在 x = 0 点处取得边界点(sharp point) 的分布。我们可以使用指数分布来达到这一目的:
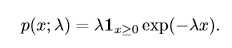
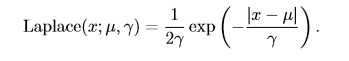
在一些情况下,我们希望概率分布中的所有质量都集中在一个点上。这可以通过Dirac delta 函数(Dirac delta function,狄拉克函数)δ(x) 定义概率密度函数来实现: \[p(x)=σ(x)\]
狄拉克函数可以被描述成在原点处无限高,无限窄的曲线,并且它的积分为1,也就是说该函数在原点处取值为\(+\infty\),其他点处为0。通过把 p(x) 定义成 δ 函数左移 ?μ 个单位,我们得到了一个在 x = μ 处具有无限窄也无限高的峰值的概率密度函数:\[p(x)=σ(x-μ)\]
Dirac 分布经常作为经验分布(empirical distribution)的一个组成部分出现:
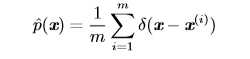
通过组合一些简单的概率分布来定义新的概率分布也是很常见的。一种通用的组合方法是构造混合分布(mixture distribution)。混合分布由一些组件 (component) 分布构成。我们在上一节中已经看过一个混合分布的例子了:实值变量的经验分布对于每一个训练实例来说,就是以 Dirac 分布为组件的混合分布。
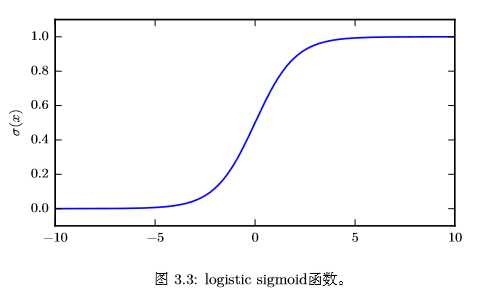
logistic sigmoid函数的表示如下:
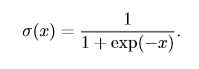
softplus函数的表示如下:
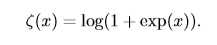
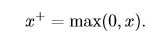
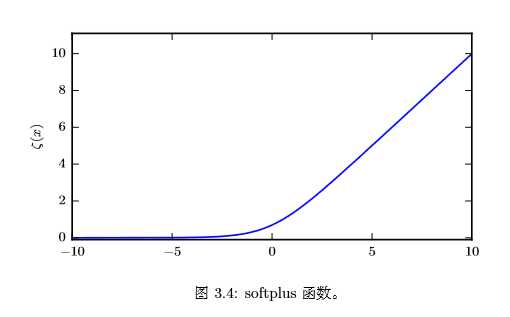
关于logistic sigmoid函数和softplus函数有一些非常有用的性质:
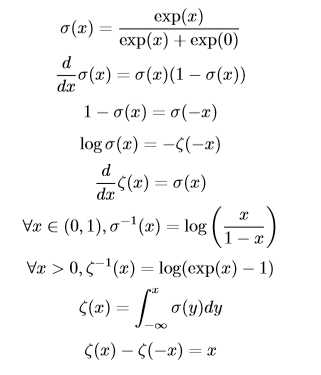
我们经常会在已知\(P(y|x)\)的时候来计算\(P(x|y)\),这时我们可以使用下面的公式:\[P(x|y)=\frac{P(x,y)}{P(y)}=\frac{P(x)P(y|x)}{P(y)}\],但\(P(y)\)有时是不知道的,我们可以使用公式\(P(y) = Σ_xP(y|x)P(x)\)来计算。
机器学习的算法经常涉及到在非常多的随机变量上的概率分布,通常这些随机变量中的直接相互作用只牵扯到非常少的变量。使用单个函数来描述整个联合概率分布是非常低效的,这时,我们可以把单个函数分解成因子相乘的形式。比如,有三个随机变量a,b,c,a影响b的取值,b影响c的取值,但a和c在b给定的情况下是独立的,则\[p(a,b,c)=p(b)p(a,c|b)=p(b)p(a|b)p(c|b)\]
这种分解可以极大地减少描述一个分布的参数数量。
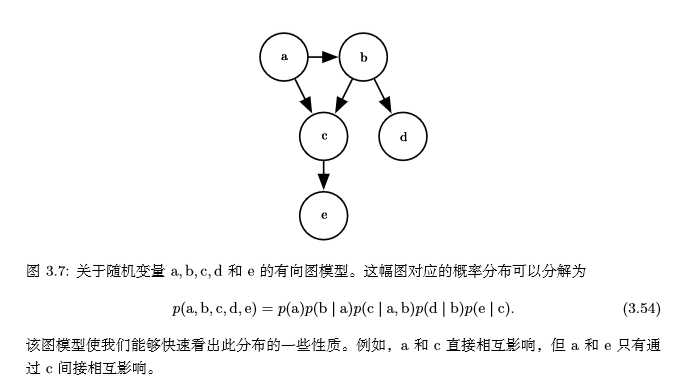
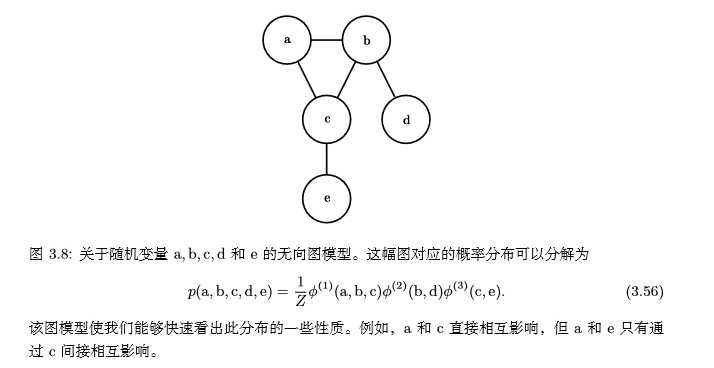
我们还可以使用图论中的图来表示这种分解,随机变量代表图中的结点,边表示随机变量间是否有联系。假设有5个随机变量a,b,c,d,e,它们对应的图如下:
标签:arp 条件 取绝对值 几何 排除 center 推理 向量 严格
原文地址:https://www.cnblogs.com/sench/p/9478284.html