标签:for href iterator new put sink getc 数组 empty
这道题可以看出来是最小割的板子题,不过因为这道题的n,m都到了1000,所以总点数是10^6,直接跑最小割会超时。
于是我们要新引入一个概念:对偶图。
我们先说一下什么是平面图。平面图就是所有的边只在顶点处相交。
比如上面的图就是一个平面图。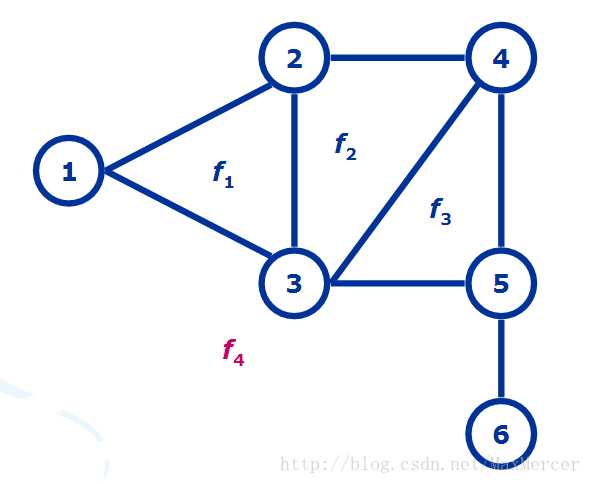
对于每一个平面图,都有与之对应的对偶图。平面图中边与边之间围成的区域叫面,最外面一个区域也被视作一个面。对偶图就是把每个平面图中的面都视为一个点,对于面与面之间的边,就在面所对应的点之间建立一条双向边,边权与原来相同。如果面的两侧都是自己,那么就连一条自环的边就可以了。
这样我们就发现一条非常重要的性质,如果我们把原点和汇点连一条边,把上半部分视为超级源点,下半部分视为超级汇点,那么我们只要跑一遍对偶图上的最短路,其数值大小即等于原图最小割。直观的理解一下,每条对偶图上的边都可以看作是在原图上的一条杠,而如果想用这些杠把整个图隔断,(最小割)这些杠一定是可以连起来的。
(如果感到难懂可以看一下dalao的图解):传送门
所以只要转化为对偶图以后,跑一遍dij就可以了。
回来看这道题,是非常明显的平面图。所以我们把它的对偶图建出来,直接跑最短路就可以了。
不过其实平面图挺难建的……而且要注意的是,转化为平面图之后点有可能会变多,数组不要开小,预处理的时候不要忘记处理。
看一下代码。
#include<cstdio> #include<cstring> #include<algorithm> #include<queue> #include<cmath> #include<set> #include<utility> #define rep(i,a,n) for(int i = a;i <= n;i++) #define per(i,n,a) for(int i = n;i >= a;i--) #define enter putchar(‘\n‘) using namespace std; typedef long long ll; typedef pair<int,int> pr; const int INF = 1e9; const int M = 2000005; int read() { int ans = 0,op = 1; char ch = getchar(); while(ch < ‘0‘ || ch > ‘9‘) { if(ch == ‘-‘) op = -1; ch = getchar(); } while(ch >= ‘0‘ && ch <= ‘9‘) { ans *= 10; ans += ch - ‘0‘; ch = getchar(); } return ans * op; } struct node { int next,to,v,from; } e[M<<3]; set <pr> q; set <pr> :: iterator it; int n,m,head[M<<1],maxflow = 0,d,dis[M<<1],ecnt,minn = INF; int source,sink; void add(int x,int y,int z) { e[++ecnt].to = y; e[ecnt].v = z; e[ecnt].from = x; e[ecnt].next = head[x]; head[x] = ecnt; } void build() { rep(i,1,n) { rep(j,1,m-1) { d = read(); if(i == 1) add(2*j,sink,d),add(sink,2*j,d); else if(i == n) add(j*2-1 + 2*(m-1)*(n-2),source,d),add(source,j*2-1 + 2*(m-1)*(n-2),d); else { add(j*2-1 + 2*(m-1)*(i-2),j*2 + 2*(m-1)*(i-1),d); add(j*2 + 2*(m-1)*(i-1),j*2-1 + 2*(m-1)*(i-2),d); } } } rep(i,1,n-1) { rep(j,1,m) { d = read(); if(j == 1) add(source,j + 2*(m-1)*(i-1),d),add(j+2*(m-1)*(i-1),source,d); else if(j == m) add(2*(m-1)*i,sink,d),add(sink,2*(m-1)*i,d); else { add(2*j-2 + 2*(m-1)*(i-1),2*j-1 + 2*(m-1)*(i-1),d); add(2*j-1 + 2*(m-1)*(i-1),2*j-2 + 2*(m-1)*(i-1),d); } } } int tot = -1; rep(i,1,n-1) { rep(j,1,m-1) { d = read(),tot += 2; add(tot,tot+1,d),add(tot+1,tot,d); } } } void dij(int s) { dis[s] = 0; q.insert(make_pair(dis[s],s)); while(!q.empty()) { pr now = *(q.begin()); q.erase(q.begin()); for(int i = head[now.second]; i; i = e[i].next) { if(dis[e[i].to] > dis[now.second] + e[i].v) { it = q.find(make_pair(dis[e[i].to],e[i].to)); if(it != q.end()) q.erase(it); dis[e[i].to] = dis[now.second] + e[i].v; q.insert(make_pair(dis[e[i].to],e[i].to)); } } } } int main() { n = read(),m = read(); if(n == 1) { rep(i,1,m-1) d = read(),minn = min(minn,d); printf("%d\n",minn); return 0; } if(m == 1) { rep(i,1,n-1) d = read(),minn = min(minn,d); printf("%d\n",minn); return 0; } source = 2*(n-1)*(m-1) + 1,sink = source + 1; build(); rep(i,1,M) dis[i] = INF; dis[source] = INF,dis[sink] = INF; dij(source); printf("%d\n",dis[sink]); return 0; }
标签:for href iterator new put sink getc 数组 empty
原文地址:https://www.cnblogs.com/captain1/p/9495437.html