标签:转换 tis ... 部分 mes 使用 直接 线性 中国剩余定理
中国剩余定理的具体描述是这样的:

给出你n个ai和mi,最后让求出x的最小值是多少。
中国剩余定理说明:假设整数m1, m2, ... , mn两两互质,则对任意的整数:a1, a2, ... , an,方程组 有解,并且通解可以用如下方式构造得到:
有解,并且通解可以用如下方式构造得到:
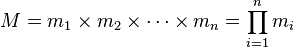 是整数m1, m2, ... , mn的乘积,并设
是整数m1, m2, ... , mn的乘积,并设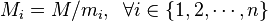 是除了mi以外的n - 1个整数的乘积。
是除了mi以外的n - 1个整数的乘积。 为
为 模
模 的数论倒数:
的数论倒数:
 的通解形式为:
的通解形式为: 在模
在模 的意义下,方程组
的意义下,方程组 只有一个解:
只有一个解: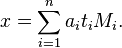
使用中国剩余定理来求解上面的“物不知数”问题,便可以理解《孙子歌诀》中的数字含义。这里的线性同余方程组是:

三个模数m1 3, m2
3, m2 5, m3
5, m3 7的乘积是M
7的乘积是M 105,对应的M1
105,对应的M1 35, M2
35, M2 21, M3
21, M3 15. 而可以计算出相应的数论倒数:t1
15. 而可以计算出相应的数论倒数:t1 2, t2
2, t2 1, t3
1, t3 1. 所以《孙子歌诀》中的70,21和15其实是这个“物不知数”问题的基础解:
1. 所以《孙子歌诀》中的70,21和15其实是这个“物不知数”问题的基础解:

而将原方程组中的余数相应地乘到这三个基础解上,再加起来,其和就是原方程组的解:
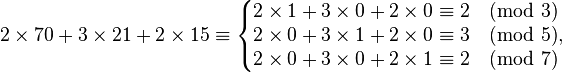
这个和是233,实际上原方程组的通解公式为:

《孙子算经》中实际上给出了最小正整数解,也就是k -2时的解:x
-2时的解:x 23.
23.
附:数论倒数 wiki
标签:转换 tis ... 部分 mes 使用 直接 线性 中国剩余定理
原文地址:https://www.cnblogs.com/zhumengdexiaobai/p/9495496.html