标签:二分 技巧 窗口 扫描 现在 multiset size dfs 递推
《Matrix》(HDU)
题意:n*m矩阵,每个点可黑可白,问有多少种方案使矩阵至少有A行B列全黑。
思路:第一反应当然是容斥,但是发现a+1行全黑的方案,并不是恰被a行全黑的方案多算a次,所以直接+1,-1,+1,-1这样的容斥系数就不可行。
而如果DP,复杂度太高,不可行。
于是考虑手推容斥系数,a行全黑的方案,被计数的次数取为([a>=A]-被更小的a计算次数)即可。
收获:对于复杂的计数问题,如果分类时,一种方案会在若干类中重复计数,可以使用推广的容斥来做。
《Always Online》
题意:给一棵带边权的点仙人掌,对于全部点对s,t,求s^t^maxflow(s,t)之和,^为异或。
思路:对于s-t路径上的树边,他的最大流量就是自己的权值。
对于s-t路径上的环,在环上路径起点和终点处断开,分成的两段各自取min,加起来就是环的最大流量。
注意到两段的min之一必为全局的min,所以环上流量的瓶颈之一已经确定,就是权值最小的边。
把这条边断开,权值加在环上的其他边上,就转成了树上的情况,按权值从大到小加边,并查集维护每一个连通分量在每一个二进制位上的答案即可。
收获:当环的某一条边对答案的贡献确定后,解题时可以把这条边割掉以转化成链。
《Daylight》
题意:给一棵树,给一棵树,每次给出点u,v和数w,查询满足Min{dist(d,u),dist(d,v)}<=w的d的数量。点数和查询都是1e5,多测,强制在线。
思路:考虑一个点d到两个点u、v距离的较大/小值,应当考虑d到uv路径中点m的距离。
结论:Max{dist(d,u),dist(d,v)}=dist(m,d)+dist(u,v)/2
证明:考虑以m为根,则d可能在:
1、m的包含u的子树
2、m的包含v的子树
3、m的其它子树
讨论一下就行了。
注意到答案就是sigma[dist(d,u)<=w]+sigma[dist(d,v)<=w]-sigma[Max<=w],而Max<=w等价于dist(m,d)<=w-dist(u,v)/2。
为了防止中点m落在边的中间,我们需要把每一条边拆成前后两条。当然通过对方向的讨论也可以不拆边。
所以问题转化成:
给点u和数w,在线查询满足dist(d,u)<=w的d的数量。
涉及路径及路径长度的问题,可以考虑点分治。
对于点分树的任意包含u的,以r为根的子树,因为u是定点,所以u到r的距离确定,故在lca(u,d)=r的前提下,d到r的距离区间也是确定的。(注意到这样的r只有log个)
所以可以预处理:对点分树中的每一棵子树,到根r距离不超过i的点有几个。经过离散化后易见时间复杂度是n log^2 n。
回答查询的时候枚举r的log种取值,对于每个r调取之前预处理的值即可。
收获:对于涉及树上两个点的问题,往往可以考虑两点之间的路径(特别地,路径中点);涉及路径及路径长度的问题,可以考虑点分治。
《Medium Pyramid Hard》
题意:有一金字塔形状的数图,底层是1~N的排列,上面每一格的数是下层相邻3格的中位数。问最顶端的数。
思路:这是一个跟数的大小关系有关的题,考虑二分答案并转化为01序列。具体地说:
1、二分答案a
2、把排列中的每个数P[i]变成[P[i]>=a]
3、看最终顶端的数是0还是1,判断a是大了还是小了。
问题转化成:底层由0、1(黑/白)组成,上面每一格的数是下层相邻3格的中位数。问最顶端的数。
我们考虑不使用金字塔图,而是方形图, 上面每一格的数是下层相邻3格的中位数(忽略出界的格子)。
发现:
1、在任何一层,对于全0或者全1的一个长度超过1的子串,如果他的左右都形如101010...,那么每往上一层,这个纯色子串就会向左右各扩张一格。
2、如果两个同色纯色子串之间没有其它纯色子串,在扩张过程中相交,则它们合并。
3、如果两个异色纯色子串之间没有其它纯色子串(易知它们之间是偶数个形如1010的元素),如果它们在扩张过程中相切,则中间的元素对半分。
所以易证,顶端元素的颜色,就是:第一层最靠近中间的纯色子串的颜色。
收获:加深了对“二分转化为01序列”的理解
《Berland Army》
核心题意:给一DAG,需要给每个点一个1~k的标号,要求后继点的标号严格小于前驱,并且1~k都要出现在标号里,一些标号已经给定,让你补全剩下的。
思路:
首先dfs两遍,预处理每一个点在所有情况下可能的最大/最小标号min和max。
发现性质:假如确定了一些点的标号,且已确定的标号d[i]在min[i]和max[i]之间,并且目前满足大小关系,则一定可以合法地补全其它。
证明的话,根据min和max的递推式,可以反向构造出方案,不多讲了。
所以好像只需要考虑限制条件min[i]<=d[i]<=max[i]?具体原因之后再说。
问题转化为:把1~k的每一个整数不重复地对应上一个区间[min[i],max[i]],使得整数被对应区间包含。
解决这个问题,可以从1扫到k,维护一个区间集合,包括了所有包含当前整数,且没有用过的区间,每次从集合里贪心地取出右端点最靠左的区间,并把他和当前整数对应上。也就是说,把这个区间所指代的结点的标号,设为当前整数。正确性易证,因为右端点不是最靠左的区间,会有更大的潜力对应上以后的整数。
为什么这样做能保持DAG上的大小关系?因为有性质:如果P是前驱,S是后继,那么max[P]>=max[S],min[P]>=min[S]。
所以,容易发现贪心过程中,P被取出一定在Q被取出之后,所以d[P]>d[Q]。
收获:DAG标号的问题中,可以用题中的min/max来取消图的限制。
《Admiral》
题意:21条战舰有6种颜色,排成金字塔形,每次可以把旗舰和相邻战舰交换位置,最终要使金字塔的每一层颜色一样。找出不超过20步的最优方案。
思路:每次可以把旗舰和左上、右上、左下、右下四者之一交换,易证不会有两次连续的交换是方向相反的(因为这两次交换会抵消),所以每次实际上只有3种交换的方向选择。
于是对20步折半搜索,用3^10枚举从初始盘面10步到达的所有状态,再反向枚举最终盘面10步到达的所有状态,在两个状态集合中找到公共元素即可。
TC SRM 589 Div1 Lev1
题意:制胡窜中,每次可以钦定两个字母s和t,并把所有s都变成t。问最少操作数使其变成回文串。
思路:串里位置对称的两个字符如果不一样,必然会被变成同一种字符,在两种字符中间连一条无向边表示。
易见最优方案是:
1、每个连通块找一个代表元
2、连通块里其他元素变成代表元
TC SRM 589 Div1 Lev2
题意:给一张三分图和染色方案,让你删掉一些结点并给剩余结点写上0或1,使得有边相连的结点标号不一样,且同色结点标号一样。问最少删几个结点。
思路:枚举颜色与标号的对应关系,易见最优方案一定是:1种颜色写0,2种颜色写1。
这样,在两个写了1的颜色之间,就会有一些边产生矛盾,而每一条这种边,必须要有一个端点被删掉,用二分图最小割找到最少的删除数量。
收获:有些问题在非二分图上难以解决的,可以用技巧转化成二分图。
TC SRM 589 Div1 Lev3
核心题意:给一长n的01串,每次可以flip一个bit,或者flip所有下标除m下取整小于d(d任选)的bit,使得最终串的前n-m位与后n-m位匹配。
思路:易知题目要求等价于,最终的串是循环串,且以m为循环节。(m较大的时候要特判)
发现如果知道了哪些块被第二种操作反转过了,那么反转过后,要做的就是用第一种操作,把所有下标模m同余的位变成一样,对每一个同余类分别贪心就能求出最小操作数。
另一方面,如果知道了最终的一个循环节长什么样,那么对所有下标除m等于d的段,可以用以下DP找到操作数:
DP[i][j]:当前在第i段,前一段是否被第二种操作反转(j=0:否 j=1:是),目前的最小操作数。
发现两个算法,复杂度一个是O(n*2^(n/m)),一个是O(n*2^m),根据n/m和m的大小关系取用这两个算法,得到最终的复杂度上界是O(n*2^sqrt(n)),能过。
收获:提出两种算法,分情况取用以降低复杂度,这种思路也能适用于指数算法。
《Monster Hunter》
题意:给一有根树,每一个点有一个怪兽,每个怪兽有值a[i]和b[i],表示如果打这个怪兽,会先扣a[i]滴血,再加b[i]滴血。主角从根节点开始,要打遍天下(对每一个点,第一次经过时会与怪兽交战),要求任一时刻血量非负,问最小的初始血量。
思路:如果忽略树上的地形限制,那么考虑贪心,把怪兽分成两类:
1、a[i]<=b[i]:打完没有损失,门槛是攻打前的血量,按a[i]升序依次打。
2、a[i]>b[i]:打完会扣血,所以一定打完第1类才会打第2类。
注意到对于第2类,初始血量扣掉a[i],加上b[i]得到最终血量,反过来考虑就是最终血量扣掉b[i],加上a[i]得到初始血量,又由于我们要最小化初始血量,根据对称大法(对比第1类),第2类怪物我们应该按照b[i]降序依次打!
那如何把地形因素加入考虑?
先把所有怪物按前述标准排序,对于第一个怪物D,一定有:
打完D的父亲结点之后,一定会紧接着打D!
这个结论,用反证法易证。
所以,既然D和D的父亲一定是紧挨着访问的,就可以把D和D的父亲捆绑(缩点),看成是一个节点。对于第二个、第三个……结点,同理。
解法框架:定义一个按照前述标准排序的堆,先把所有结点压入,每次弹出排序最靠前的结点和这个结点的父亲,把他和他父亲捆绑,计算新的a和b,再重新压入,直到只有一个结点为止。
收获:加深了对“树上父子合并”类贪心的理解。
《Contact ATC》
题意:数轴上有n个点,都在向原点以不同速度移动,有[-w,w]之间的未知恒定风速,风速会加在点的运动速度上,保证风速的绝对值小于点运动速度的绝对值。问有多少点对,在一定风速下会在原点相遇。
思路:发现两个点A、B可能在原点相遇的充要条件是:
风速等于w时A先于B到达原点;
风速等于-w时B先于A到达。
(证明:介值定理)
所以对每个点找到风速为w、-w时的到达时间,转化为二维数点,随便怎么做都行,比较方便的是用离线+BIT。
《Magic Multiset》
题意:有若干multiset排成一行,一个multiset如果插入一个未曾出现的元素就直接插入,如果插入一个已经出现的元素,里面的每个元素数量都会翻倍。让你支持区间的每个multiset插入元素,和查询区间multiset的大小之和。
思路:由于insert和duplicate是截然不同的操作,我们考虑一次插入操作,会使哪些multiset执行了insert,哪些执行了duplicate,即哪些multiset已经包含了插入的元素。
对每一种元素,用集合维护哪些连续的multiset区间全部包含了这个元素。对于插入操作,暴力跑遍集合中,本次操作涉及的multiset区间,并作修改。
为了维护multiset大小,需要实现一棵支持区间+1,区间*2,区间求和的线段树。
复杂度证明:集合中,一次操作最多产生3个额外区间,且每个区间只会被插入一次、删除一次。故总的区间修改次数是线性的。
《Pollywog》
题意:有排成一列的n个石头,一开始前x个上面有青蛙,每次最左侧的青蛙会向右跳不超过k步,不能有青蛙在同一石头上,要使得最终青蛙在后x个石头上,问最小代价。跳不同距离有不同代价,另外落在特殊的q块石头上有额外代价。n<=1e8,x,k<=8,q<=25
思路:注意到在任一时刻,易证最靠左和最靠右的青蛙,位置差距不超过k。
于是DP,对于连续的k块石头(可以看作一个“窗口”),对“第i块是否被占据”状压,每次把窗口向右滑动一位,并且让最左的青蛙向右跳,维护最小代价。
注意到这个DP可以用矩阵快速幂优化,原因是把普通的矩阵乘法中,乘换成加,加换成取min,易证依然存在结合律。
但是如果特殊石头在窗口内,就只能暴力转移。易证需要暴力转移的最多只有200次。
收获:推广的矩阵乘法
《Arkady and Rectangles》
题意:平面上依次放入n个颜色不同的矩形(颜色按放置顺序为1~n),后放的可能覆盖先放的。问最后平面上可见的颜色个数。
思路:
试过各种数据结构都不能在线维护,又发现我们只对最终的状态感兴趣,所以考虑从上往下扫描线。
那么就需要支持以下几种事件:
1、插入一条未被计入过答案的线段
2、删除一条线段
3、弹出一条未被计入过答案且可见的线段
4、插入一条被计入过答案的线段
用线段树维护,插入线段时把它拆成log个小段,存储在线段树结点里,用集合colors维护当前结点的线段。
为了支持第3种操作,维护一个值max,表示当前(即所在结点和后裔的colors集合)未被计入过答案且可见的线段中,颜色编号最大的。
但是注意到子节点的短线段可能连成一片,覆盖掉自己的长线段L(这个其实是大多数错误算法的核心问题),而且出现这种情况的充要条件是,子结点中,颜色编号最小的可见线段都大于L。
所以为了处理这种情况,还需要再维护一个值min,表示当前可见线段中颜色编号最小的(不管有没有被计入答案)。
那么线段树的pull_up大概是这么写的(伪代码写得不伦不类抱歉了):
max=colors.max
if counted[max] OR Min{son[0].min, son[1].min}>max then:
max=-1
else if Max{son[0].max, son[1].max}>max then:
max=Max{son[0].max, son[1].max}
min=colors.max
if Max{son[0].min, son[1].min}>min then:
min=Max{son[0].min, son[1].min}
(注意到标记不下放,所以没有push_down)
这样每做完一次修改,就对查询根节点的max,如果不是-1,就:
1、把max对应的线段计入答案
2、把max对应的线段打上“已被计入答案”的标记(count[root.max]=1)
3、把包含max对应线段的子段的所有结点,和他们的祖先都依次重新pull_up。
被这题虐完就再也不敢说自己会线段树
收获:数据结构题什么千奇百怪的量都可能要维护……大胆设元总没错。
《Don‘t Exceed》
题意:有n个[0,1]之间的实随机变量,要求前i个的和不超过x[i],问所有要求同时满足的概率。
思路:根据套路,应该用定积分!(好像概率题除了定积分我也不会什么了)
让Fi(x)表示:对于前i个变量,条件“前i-1个变量都满足题目要求且第i个变量不超过x”达成的概率。
那么有: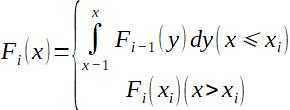
可以发现Fi是一个分段函数,而且每一段都是一个多项式!
比较方便的维护方法是,预处理出所有段的端点,每次直接用法则,求出Fi的原函数再求出定积分即可。
注意到在任何时刻,分段函数的段的端点,只可能形如x[i]+k,其中k为不超过n的非负整数。
所以在任何时刻,段的数量为O(n^2),可证最终复杂度为O(n^5),可过。
说起来还好,写起来烦死人……
djq:珍爱生命,远离积分
JSOI2018 D3T1
题意:给一棵树,在一个结点上放一个监听器可以监听所有邻居。给定监听器数量,问监听整棵树的方案数。
思路:裸的DP比较显然,
dp[i][j][k][l]:子树i放了j个监听器,k=0/1表示i是否被监听,l=0/1表示i是否有监听器。
转移的时候对于所有子节点跑一遍背包(实则是deg[i]次暴力卷积)即可,复杂度n*k^2,估计有40分。
为了降常我们想到一个玄学优化,注意到j<=size_of_subtree[i] ,所以把j这一维改成可变长的,卷积的时候只枚举到两边的size即可。
然后就过了。
这就是我在考场经历的事情,想了半个下午才想到复杂度证明。
证明,把子树分为两类:
1、小子树:大小不超过k
2、大子树:大小超过k
特别地,如果一个大子树的儿子,都是小子树的根,称这个大子树为“极小大子树”。
特别地,如果一个小子树的父亲,是大子树的根,称这个小子树为“极大小子树”。
易证极小大子树都是不相交的,所以最多有n/k棵极小大子树。
易见所有大子树的根都是连通的,且形成了一棵树T‘,那么T‘的叶节点一定都是原树的极小大子树的根。所以T‘有不超过n/k个叶节点。
注意到,如果一个点只有一个儿子,那么他的转移复杂度是O(k)的,可以忽略不计。
所以,不妨假设T‘的每个点都有至少两个儿子。
那么可证,T‘的节点数不超过叶节点数的两倍,即不超过n/k。T‘的每个节点转移复杂度是k^2,所以总复杂度是O(nk)。
再考虑小子树的转移。
如果结点v有两个子树s[0]和s[1],由于用了可变长优化,v的转移复杂度不超过size[s[0]]*size[s[1]]。
这个值相当于从s[0]中选一个点,再从s[1]中选一个点,这样的二元组数量?
这样的二元组有一个性质:二元组里两个点的lca是v。
(对于有超过2个子树的情况结论也一样,不多赘述)
又因为对于确定的二元组,他的两点的lca是确定的,所以他会在哪一次转移中被计入复杂度,是唯一确定的。
所以在一个极大小子树s中,总的转移复杂度不超过size[s]^2,不超过size[s]*k。
又因为易证极大小子树不相交,所以,所有的极大小子树的转移复杂度之和,不超过total_size*k,即不超过nk。
故总时间复杂度为O(nk),可过。
出题人出这种复杂度分析题不怕被选手打吗
收获:复杂度分析的技巧。
JSOI2018 D3T2
题意:给一棵点仙人掌,对于点集的每一个子集,你需要求出其斯坦纳树大小,并输出所有答案的总和。
思路:类似always online,考虑每条树边和每个环对答案的贡献。
树边的贡献显而易见,就是两侧子树大小作为2的指数,再相乘。
对于特定的环,考虑如果以这个环为基环的话,环上每个点挂的子仙人掌。
对于每一个子仙人掌,如果它里面有结点被选进集合里,就把基环在这个点处断开。
最后断出来的若干段,把最长的一段去掉,其它加起来就是对答案的贡献。
所以考虑DP,dp[i][j]:当前最后一次断开在环上第i个点,最长段长度为j的方案数。
选择一个子仙人掌v里的点,方案数为2^size[v]-1,用前缀和转移即可。
收获:对于仙人掌问题,把树边和环分开来考虑问题。
JSOI2018 D3T3 sol yjz
题意:平面上有一个圆心为原点的圆,和n个点d[0]~d[n-1]。让你找到圆的一组n等分点p[0]~p[n-1],并且找到d与p的一组完美匹配,使得匹配的两点距离的最大值最小。
思路:首先根据套路应该先二分答案ans。
二分答案之后,我们关心的就只是可行解,而非最优解(考场上我就困在最优解里出不来了)。
对于d里的每一个点,都会有一个可行区间与之对应,表示若theta在此区间内,则存在一个距离不超过ans的等分点与之对应。
如果确定了等分点的位置,剩下的就是跑一遍二分图匹配的事了。
注意到如果存在可行解,一定有一组解的theta,是卡在某一个d中的点的区间端点上的。
而且,如果theta变化一个很小的量,二分图改变的边也是很少的。
所以把所有区间的端点(总共O(n)个)排序,theta从头扫到尾,每次跑一遍匹配即可。为了优化,加边/删边时可以用加流/退流完成,由于退流总共影响的的边数是O(n)的,所以复杂度可以接受。
收获:网络流图连续变化的时候,可以在变化过程中维护最大流;最优化问题首先考虑二分。
JSOI2018 D3T3 sol zyd
题意:同上
思路:会乱搞还写什么正解啊……
注意到最优答案是关于theta的连续函数,这题长了一脸乱搞相啊!
考虑爬山,随机一个theta的初始值,钦定一个步长,每次贪心地看往左跳还是往右跳还是不动,步长随时间指数下降。
然后只要你能拥有z神的调参神力,就能过了!
收获:乱搞大法好!
《Card Game》
题意:给n 张卡片,每张卡片正反面各有一个数。问至少要翻转多少张,才能使向上的数各不相同,并求方案数。
思路:(只知道做法,就只能盲目猜测一下想到做法的过程了)
向上的数各不相同……意思是每个点最多只在一张卡的朝上一面出现?
考虑怎么表示一张卡(a,b)朝上的是a,发现可以从a向b连边?
然后发现问题转化成,反转尽可能少的边使每个点出度不超过1?
出度不超过1……基环树?
这样构出的图,考虑一个弱连通分量。可证存在合法方案,等价于这个弱连通分量的基图是树或者基环树。
如何求最优方案和方案数?
对于基环树:树边的方向唯一确定,环上边的方向分顺/逆时针(分方向只是为了方便考虑)两种,讨论一下即可。
对于树:易见如果根节点钦定了,方案一定是把每条边改到指向根的方向。那么随便选一个根,再用换根法求出对于每一个结点作为根的答案即可。
最终的答案就是所有弱连通分量操作数相加,方案数相乘。
收获:应用问题到图论的转化方法,并不是单一的那几种经典模型(比如2sat),需要有一定创造性。
标签:二分 技巧 窗口 扫描 现在 multiset size dfs 递推
原文地址:https://www.cnblogs.com/turboboost/p/2018-Summer-Collection.html