CF1016C Vasya And The Mushrooms 题解

标签：span   yii   pre   color   car   第一个   而且   agg   后缀   

这道题一眼就是一个DP（大雾），但题目中有一句很有趣的话

“He wants to visit all the cells exactly once and maximize the total weight of the collected mushrooms.”

也就是每个格子必须且只能经过一次，而且只有两派格子，所以是不是一目了然的只有两种行走路线。

其实不然，你还可以这么走

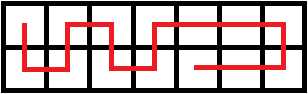或者，这么走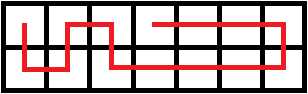

也就是把前两种行走方式结合一下

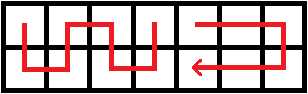
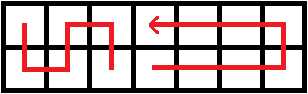
不过也没有变得不可做，因为一定是先用第一种行走方式，再接第二种；不可能存在先走第二种，再第一种的情况（都已经拐回去了，还走啥啊）。所以枚举一下从何时开始更换行走方式即可。这两种行走方式吃到的蘑菇都可以先预处理出来。

a1是第一行的蘑菇生长率，a2是第二行的

因为观察到无论从何时改变行走方式，都可以看成是在走完一个整列后再改变，所以所有的数组都是以列数作为下标的。

首先预处理蛇形行走方式：

两行两行处理，每次走一个U型，要注意蘑菇不是从第1秒开始长的（其实是时间是从 0 s 开始记的，不过一样哈）

init_b(){
    //b[i]表示蛇形在取完第i列的格子的蘑菇后的 
    //第一个格子为第1s(但不吃蘑菇)
    //这个格子蘑菇数为(i-1)*a 
    int s=0;
    for(int i=1;i<=n;i+=2){
        s+=a1[i]*(i*2-2);
        s+=a2[i]*(i*2-1);
        b[i]=s;
        s+=a2[i+1]*(i*2);
        s+=a1[i+1]*(i*2+1);
        b[i+1]=s;
        //走了一个U型 ↓→↑
    }//走了一个S型 
}

再预处理环形行走方式：

这样的一条路可以看成是的一条路加上蓝色的两个格子的蘑菇。

不过原来路上的每只蘑菇都多生长了 1 s，所以要加一个“后缀和”。

init_S(){
    //S[i]表示从第i列(从左往右数)以及右边的半圈的蘑菇生长率之和 
    int s=0;
    for(int i=n;i>=1;i--)
    s+=a1[i]+a2[i],S[n-i+1]=s;
}

如果是从上绕到下，上面的格子生长时间是1s，下面的格子生长时间是后面的两列格子数+上面的一个格子=（l*2+1），l 是后面的长度；

CF1016C Vasya And The Mushrooms 题解

标签：span   yii   pre   color   car   第一个   而且   agg   后缀   

原文地址：https://www.cnblogs.com/jzzcjb/p/9496661.html