标签:出现 推理 判断 技术 ima 分享图片 zab 第一个字符 kmp
假设要求"abcabcabzabc"的next表:
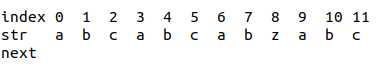
首先如果在第一个字符失配,那么显然还从第一个字符找就可以.因此next[0]=0.(这里跟很多博客说的不太一样,很多kmp实现里next[0]=-1,因为他们的思路是把-1看成终止符,意思是"next跳到这里就不要再跳了",不过其实0也可以做终止符,只要判断next[i]==i就停止)
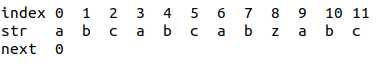
为了研究一般情况下next怎么填,我们先顺势填上几个,造成一种我们填到一半的情况.

现在要研究的问题是"如果第5位失配该跳到哪里",等效问题是"区间[0,5)上的最长公共前后缀长度+1".
看已有的答案:我们已有next[4]表示"区间[0,4)上的最长公共前后缀长度+1".图形化表述一下:

现在要想求下一位的最长公共前后缀,肯定要从上一个最长的开始找,也就是判断

所以就是判断str[5-1]==str[next[5-1]]是否成立.若成立,则新的最长公共前后缀就找到了,即
str[0 : next[5-1]+1]
若不成立呢?那就要再往前跳着找,直到找到开头为止(一直都不匹配的话只好从头开始搜)
举个例子:
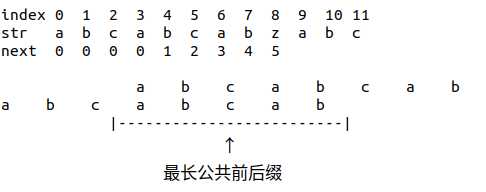
现在要求第9位的最长公共前后缀,即在8的基础上再加一位,判断str[9-1]==str[next[9-1]]是否成立.这里显然不成立.

这说明要找的最长公共前后缀不是这里,应该找比现在这个更短而又尽量长的最长公共前后缀.怎么找呢?
首先要发现一个条件:由于str[0 : next[9-1]+1]与str[9-next[9-1]-1 : 9]是最长公共前后缀关系,它们相等.
现在要找的是"比str[0 : next[9-1]+1]短的,str[9-next[9-1]-1 : 9]的最长公共前后缀"
由于上述命题里的str[0 : next[9-1]+1] == str[9-next[9-1]-1 : 9]],因此上述命题变为
"比str[0 : next[9-1]+1]短的,str[0 : next[9-1]+1]的最长公共前后缀"
注意到"与str[0 : next[9-1]+1]成前后缀关系的串"显然比str[0 : next[9-1]+1]更短,命题变为
"str[0 : next[9-1]+1]的最长公共前后缀"
问题出现递归.
总结一下,上面的推理得出的结论是:
要求"str[0 : i]的最长公共前后缀",若str[i-1]==str[next[i-1]],则找到答案;若不等,则问题变为
"str[0 : next[i-1]+1]的最长公共前后缀"
但是现在这个递归算法写起来还不够方便,还有一个小优化:
首先把上面的算法改成自然表述,听起来形象一些:要找当前字符失配后跳到哪,只需从前一个字符开始不断地往前跳,并在每次跳后检查"落地点"字符与当前字符是否相等,若相等则停止.
上述说法中"从i往前跳"意思显然是从i到next[i].
这里有一个小结论,不再证明,很显然:
若已求出next[i],正要计算next[i+1],那么i+1往前跳跃的终止点一定小于等于i跳跃的终止点+1,即next[i]+1,且i+1往前跳跃时一定经过next[i]+1.
(非要证明的话还是和刚才一样用最长公共前后缀)
由于这个结论,求每个next[i]时可以直接从next[i-1]+1开始往前跳,直到停止.
总结起来,结论是:
要求"str[0 : i]的最长公共前后缀",只需从next[i-1]开始,不断向前跳,并每次检查str[i-1]==str[跳跃点]是否成立,若成立则停止.
标签:出现 推理 判断 技术 ima 分享图片 zab 第一个字符 kmp
原文地址:https://www.cnblogs.com/ArrowKeys/p/9496610.html