标签：消元   size   www.   引入   关系   inter   操作   通过   html   

上接 梯度寻优

扩展:

• 机器学习中的几个概念的关系
• 梯度相关代码

逐次逼近法

问题 1: \(Ax = b\)

对于问题 1, 当 \(A\) 的阶数很大, 且零元素很多的大型稀疏矩阵方程组, 使用主元消去法求解将是一个很大的挑战. 为此, 逐次逼近法 (或称为迭代法) 应运而生.

下面我们来看看迭代法的具体操作:

首先将 \(Ax=b\) 改写为 \(x = Bx + f\), 使用公式:

\[ x^{k+1} = Bx^k + f \]

其中 \(k\) 为迭代次数 \((k=0, 1, 2, \cdots)\)

逐步代入求近似解的方法称为迭代法.

若 \(\underset{k \to \infty}\lim x^k\) 存在 (记作 \(x^*\)), 称此迭代法收敛, 显然 \(x^*\) 就是方程组的解, 否则称此迭代法发散.

研究 \(\{x^k \}\) 的收敛性

引入误差向量:
\[ ε^{k+1} = x^{k+1} - x^* \]

得到
\[ ε^{k+1} = (Bx^k + f) - (Bx^* + f) = Bε^k = B^kε^0 \]

故而, 要研究 \(\{x^k \}\) 的收敛性, 只需要研究 \(\underset{k \to \infty}\lim ε^k = 0\) 或 \(\underset{k \to \infty}\lim B^k = 0\) 满足的条件.

下面以 python 的形式呈现迭代的结果:

import numpy as np

%pylab inline

Populating the interactive namespace from numpy and matplotlib

求解方程组 \(Ax=b\)

消元法

A = mat([[8, -3, 2], [4, 11, -1], [6, 3, 12]])
b = mat([20, 33, 36])
result = linalg.solve(A, b.T)
print(result)

[[3.]
 [2.]
 [1.]]

迭代求原方程组的解：\(x^{k+1}=B x^k+f\)

B = mat([[0.0, 3.0 / 8.0, -2.0 / 8.0], [-4.0 / 11.0, 0.0, 1.0 / 11.0],
         [-6.0 / 12.0, -3.0 / 12.0, 0.0]])
m, n = shape(B)
f = mat([[20.0 / 8.0], [33.0 / 11.0], [36.0 / 12.0]])

error = 1.0e-7  # 误差阈值
steps = 100  # 迭代次数
xk = zeros((n, 1))  # 初始化 xk = x0
errorlist = []  # 记录逐次逼近的误差列表
for k in range(steps):  # 主程序
    xk_1 = xk  # 上一次的 xk
    xk = B * xk + f  # 本次 xk
    errorlist.append(linalg.norm(xk - xk_1))  # 计算并存储误差
    if errorlist[-1] < error:  # 判断误差是否小于阈值
        print(k + 1)  # 输出迭代次数
        break
print(xk)  # 输出计算结果

18
[[2.99999998]
 [2.00000003]
 [1.00000003]]

绘制误差收敛散点图

def drawScatter(plt, mydata, size=20, color=‘blue‘, mrkr=‘o‘):
    m, n = shape(mydata)
    if m > n and m > 2:
        plt.scatter(mydata.T[0], mydata.T[1], s=size, c=color, marker=mrkr)
    else:
        plt.scatter(mydata[0], mydata[1], s=size, c=color, marker=mrkr)

matpts = zeros((2, k + 1))
matpts[0] = linspace(1, k + 1, k + 1)
matpts[1] = array(errorlist)
drawScatter(plt, matpts)
plt.show()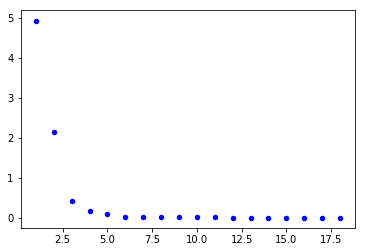

如图, 可以看出误差收敛很快, 从第四次就开始接近最终结果, 后面的若干次迭代都是对结果的微调.

通过误差收敛与否判断解的存在性, 只要误差能够收敛, 方程组就会有解, 但若目标函数是非线性的, 为了更快的收敛, 我们需要找到收敛最快的方向 (梯度方向).

梯度寻优 (二)

标签：消元   size   www.   引入   关系   inter   操作   通过   html   

原文地址：https://www.cnblogs.com/q735613050/p/9498022.html