标签:不可 name code class size 一个 ring 修改 continue
小明在旅游的路上看到了一条美丽的河,河上有许多船只,有的船只向左航行,有的船只向右航行。小明希望拍下这一美丽的风景,并且把尽可能多的船只都完整地拍到一张照片中。
小明位于河的边上,并且可以在河边的任意位置进行拍照,照相机的视野恰好为90度角,只能以垂直于河边的方向进行拍照。河上的船只全都可看作是平行于河边的一条线段,跟河边的距离各不相同,有的正在向左移动,有的正在向右移动,但移动速度恰好都是一样的。小明可以等待恰当的时间让尽量多的船只都走进照相机的视野里,你不需要考虑船只之间会互相遮挡视野的情况。
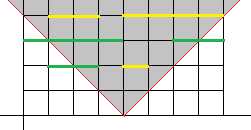
如图,阴影部分是相机放在坐标4的时候的摄像范围,绿色的线段是向右的船只,黄色的线段是向左的船只。1秒以后,可以同时排到5艘完整的船。
现在的问题是,小明可以任意的选择拍摄的地点和时间,问:他最多能一次性拍到多少艘完整的船?
首先我们发现原本的题意是一个二维的平面,但是长度最长有 2 * 10 ^ 6 显然,用二维的做法显然是不可以的。
我们要想一想怎么才能把这道题转化为一个一维的问题:
其实,假设一条船净值在一个地方,那我们在岸上能完整看到它的范围就知道了,显然这个范围是和船的长度和距离岸边的长度共同决定的。如下图所示:
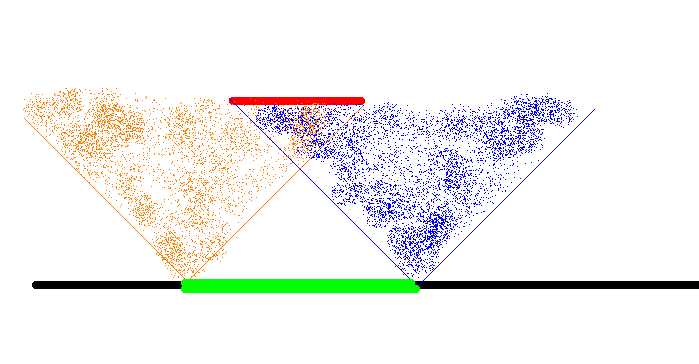
假设红色是船,黑色是岸,绿色就是可以完全看见船的范围了。
我们很容易可以想到,要将两个方向的船分开处理。我们利用差分和前缀和就可以分别处理出来某个点上可以看到的向右行驶的船和向左行驶的船的数量,又因为要能同时看到向左的船和向右的船,所以选择的向右的位置一定在想做的位置的左边,这样,船一定会相遇,但相遇在哪里我们就不关心了。利用一个数组简单处理一下就可以了。
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 using namespace std; 6 const int maxn=1e6+100000; 7 int n; 8 int chafeny[2*maxn],chafenz[2*maxn]; 9 int hey[2*maxn],hez[2*maxn]; 10 int main(){ 11 int T; 12 scanf("%d",&T); 13 for(register int t=1;t<=T;t++){ 14 memset(chafeny,0,sizeof(chafeny)); 15 memset(chafenz,0,sizeof(chafenz)); 16 memset(hey,0,sizeof(hey)); 17 memset(hez,0,sizeof(hez)); 18 scanf("%d",&n); 19 for(register int i=1,x,y,z,d;i<=n;i++){ 20 scanf("%d%d%d%d",&x,&y,&z,&d); 21 x+=maxn; 22 y+=maxn; 23 int disx=y-z,disy=x+z; 24 if(disx>disy)continue; 25 if(d==1){ 26 chafeny[disx]++; 27 chafeny[disy+1]--; 28 } 29 else { 30 chafenz[disx-1]--; 31 chafenz[disy]++; 32 } 33 } 34 int ans=0; 35 hey[0]=max(hey[0],chafeny[0]); 36 for(register int i=1;i<maxn*2;i++){ 37 chafeny[i]=chafeny[i-1]+chafeny[i]; 38 hey[i]=max(hey[i-1],chafeny[i]); 39 } 40 hez[maxn*2-1]=max(hez[maxn*2-1],chafenz[maxn*2-1]); 41 for(register int i=maxn*2-2;i>=0;i--){ 42 chafenz[i]=chafenz[i+1]+chafenz[i]; 43 hez[i]=max(hez[i+1],chafenz[i]); 44 ans=max(ans,hez[i]+hey[i]); 45 } 46 printf("Case #%d:\n",t); 47 printf("%d\n",ans); 48 } 49 }
标签:不可 name code class size 一个 ring 修改 continue
原文地址:https://www.cnblogs.com/Fang-Hao/p/9498588.html