标签:png ons ica 微积分 algo ESS 算法 imu display
计算机无法通过有限多的位来表示无限多的实数,当我们在计算机中表示一个实数时,几乎总会存在一些误差,在许多情况下,这被称为舍入误差(指运算得到的近似值和精确值之间的差异)。舍入误差会导致一些问题,特别是进行多次运算的时候。即使是理论上可行的算法,如果在设计时没有考虑最小化摄入误差的累积,在实践时也可能导致算法失效。
当接近与0的数被四舍五入为0时发生下溢,这可能造成算法失效,把该接近于0的数当做分母就会发生。举个例子,在机器学习中经常会遇到概率预算,而概率都是介于0和1之间的数,假如一个事件发生的概率为0.1,则10个0.1相乘就非常接近于0了。
当非常大的数被认为是\(+\infty\)或者\(-\infty\)时发生上溢,这同样会造成算法失效。
必须对上溢或者下溢进行数值稳定的一个例子是softmax函数。softmax 函数经常用于预测与 Multinoulli 分布相关联的概率,其定义为:
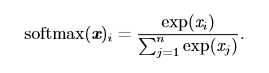
1/n。但当x中的值\(x_i\)都为很小的负数时,\(exp(x_i)\)的值就会接近0,从而发生下溢,这意味着softmax函数的分母会变成0,出现除0的错误;当x中的值\(x_i\)都为很大的正数时,\(exp(x_i)\)也会变得非常大,可能会超出计算机所能表示的最大数,从而发生上溢,导致最后的结果未定义。条件数用来衡量函数相对于输入的微小变化而变化的快慢程度。高条件数的问题被称为病态的。输入被轻微扰动而迅速改变的函数对于科学计算来说可能是有问题的,因为输入中的舍入误差可能导致输出的巨大变化。
考虑函数\(f(x)=A^{-1}x\),当\(A∈\mathbb(R)^m×n\)具有特征分解时,其条件数定义为:
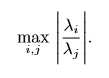
大多数深度学习算法都涉及到某种形式的优化。优化是指改变x以最小化或最大化函数f(x)的任务。我们通常最小化f(x)指代大多数最优化问题,最大化可以通过最小化-f(x)得到。
我们把要最小化或最大化的函数称为目标函数(objective function)或准则(criterion)。当我们对其进行最小化时,我们也把它称为代价函数(cost function)、 损失函数(loss function)或误差函数(error function)。
我们通常使用一个星号上标*来表示最小化或最大化函数的x值,如\(x^*=arg\;min\;f(x)\),arg的意思是获取参数,所以该式的意义是获取f(x)取最小值时的x值。
函数\(y=f(x)\)的导数记为f‘(x)或者dy/dx。导数f‘(x)代表f(x)在x处的斜率。在二元函数z=f(x,y)中,把y固定(也就是把y看成常数),这时对x求导,称为z对x的偏导数,记为\(?z/?x\)或者\(?f/?x\)或者\(▽_xf(x)\)。
在微积分里面,对多元函数的参数求?偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。比如函数f(x,y)的梯度为\([?f/?x, ?f/?y]^T\),简写为\(grad f(x,y)\)或者\(▽f(x,y)\)。在点(\(x_0,y_0)\))处的梯度就是\(▽f(x_0,y_0)\)。梯度从几何意义上讲,就是函数增加最快的方向。
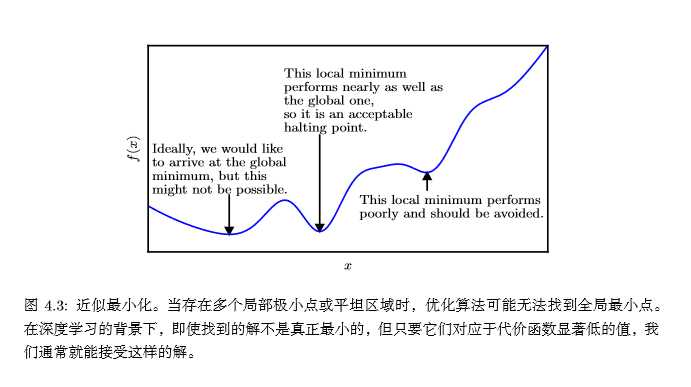
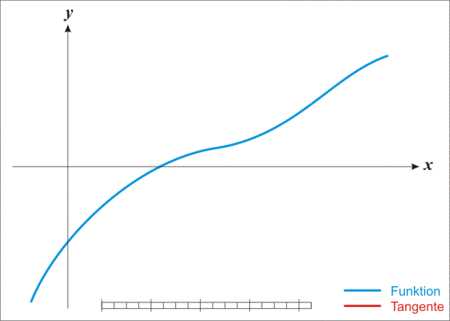
导数对于最小化一个函数很有用,因为它告诉我们如何更改 x 来略微地改善 y。例如,我们知道对于足够小的 ? 来说,f(x??sign(f′(x))) 是比 f(x) 小的(sign函数定义)。因此我们可以将 x 往导数的反方向移动一小步来减小 f(x)。这种技术被称为梯度下降 (gradient descent),下图给出了梯度下降的一个例子:
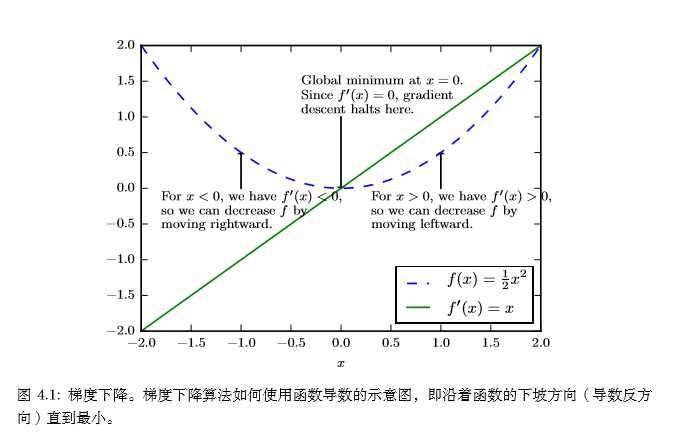
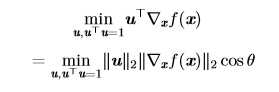
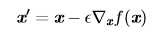
有时我们需要计算输入和输出都为向量的函数的所有偏导数。包含所有这样的偏导数的矩阵被称为 Jacobian矩阵。。具体来说,如果我们有一个函数: \(f : \mathbb{R}^m →\mathbb{R}^n\),f的雅克比矩阵 \(J∈\mathbb{R}^{n×m}\) 定义为: \[J_{i,j}=\frac{?}{?x_j}f(x)_i\]
也就是说,雅可比矩阵是函数的一阶偏导数以一定方式排列成的矩阵。举个例子,有\(\mathbb{R}^4\)的f函数:
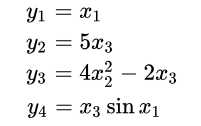
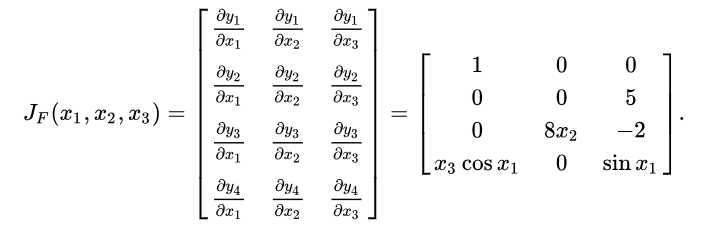
当函数具有多维输入时(有很多变量),函数有很多二阶偏导数,我们可以将这些二阶偏导数合并成一个矩阵,称之为Hessian矩阵(海森矩阵)。Hessian 矩阵 \(H(f)(x)\) 定义为 :
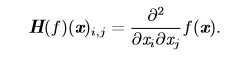
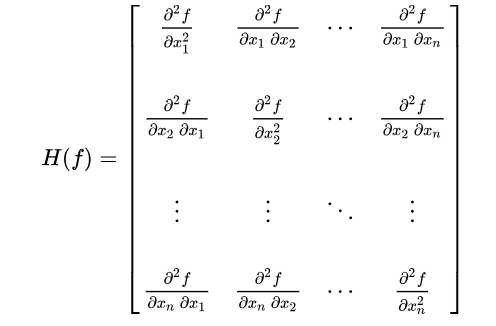
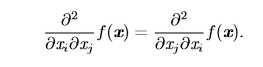
我们可以通过(方向)二阶导数预测一个梯度下降的步骤表现的有多好。我们在当前点\(x^{(0)}\)处作\(f(x)\)的近似二阶泰勒级数展开:
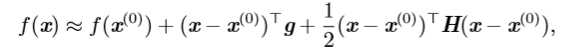
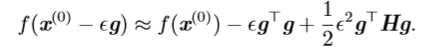
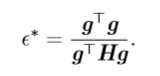
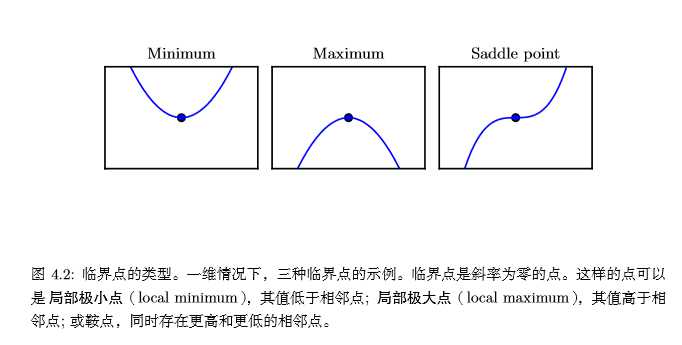
我们可以根据二阶导数的正负情况来判断一个临界点是局部极大值点、局部极小值点或者鞍点,这就是所谓的二阶导数测试。当\(f'(x)=0\)时,说明x是一个临界点,若二阶导数\(f''(x)>0\),则说明\(f'(x)\)在x的右边是递增的,因为\(f'(x)=0\),所以x右边的导数均为正,所以\(f(x)\)在x右边单调递增,x左边的导数为负,所以\(f(x)\)在x左边递减,则x为局部极小值点;同理当二阶导数\(f''(x)<0\)时,x为\(f(x)\)的局部极大值点;当二阶导数\(f''(x)=0\)时,x可以是一个鞍点或平坦区域的一部分。
上面讨论的函数只有一个未知数,我们通过函数二阶导数的正负即可判断临界点的情况。当函数有多个参数时,我们需要检查该函数所有的二阶导数,也就是海思矩阵(Hessian矩阵)。一元函数二阶导数的正负对应海思矩阵特征值的正负。所以有:在临界点处(梯度\(▽_xf(x)\)=0),若海思矩阵的特征值全为正(正定的),则该临界点是局部极小值点;若海思矩阵的特征值全为负(负定的),则该临界点是局部极大值点;如果海思矩阵的特征值中至少有一个正的并且至少有一个负的,那么 x 是 f 某个横截面的局部极大点,却是另一个横截面的局部极小点,见下图:
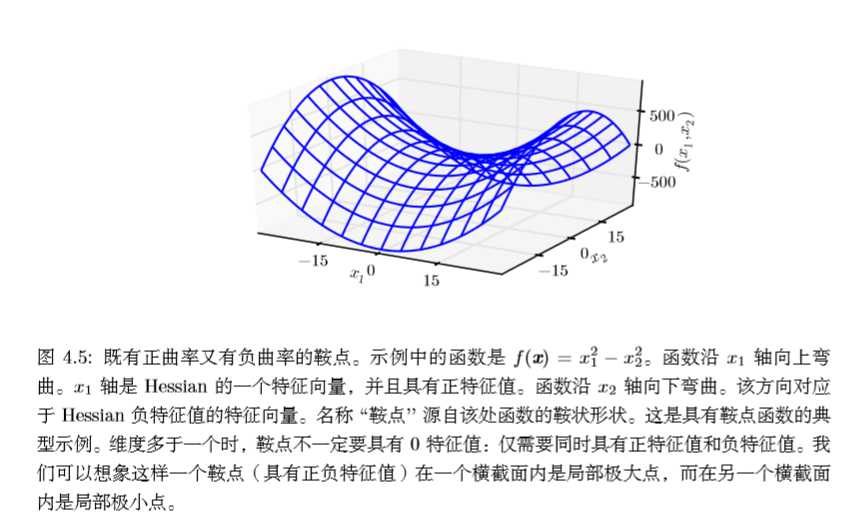
多维情况下,单个点处每个方向上的二阶导数是不同的。Hessian 的条件数(在上文中,矩阵条件数定义为最大和最小特征值之比)衡量这些二阶导数的变化范围。当 Hessian 的条件数很差时,梯度下降法也会表现得很差。这是因为一个方向上的导数增加得很快,而在另一个方向上增加得很慢。梯度下降不知道导数的这种变化,所以它不知道应该优先探索导数长期为负的方向。病态条件也导致很难选择合适的步长。步长必须足够小,以免冲过最小而向具有较强正曲率的方向上升。这通常意味着步长太小,以致于在其他较小曲率的方向上进展不明显。我们可以使用牛顿法来解决这个问题。
先来看一下使用牛顿法求解一元函数的零点。首先我们选择一个接近\(f(x)\)零点的值\(x_0\),计算\(f(x_0)\)和\(f'(x_0)\),然后求出过点\((x_0, f(x_0))\)且斜率为\(f'(x_0)\)的直线与x轴的交点坐标,也就是求如下方程的解:
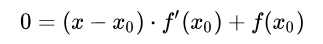
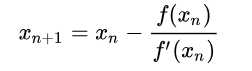
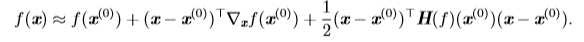
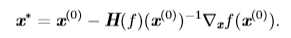
有时候,在 \(x\) 的所有可能值下最大化或最小化一个函数 \(f(x)\) 不是我们所希望的。相反,我们可能希望在 \(x\) 的某些集合 \(\mathbb{s}\) 中找 \(f(x)\) 的最大值或最小值。这被称为约束优化(constrained optimization)。在约束优化术语中,集合 S 内的点 x 被称可行点(feasible point)。
标签:png ons ica 微积分 algo ESS 算法 imu display
原文地址:https://www.cnblogs.com/sench/p/9495140.html