标签:ADG png == copy orange class 更新 不用 回溯
有 $n$ 个同学(编号为 $1$ 到 $n$ )正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象,其中,编号为 $i$ 的同学的信息传递对象是编号为 $T_i$ 的同学。
游戏开始时,每人都只知道自己的生日。之后每一轮中,所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象(注意:可能有人可以从若干人那里获取信息, 但是每人只会把信息告诉一个人,即自己的信息传递对象)。当有人从别人口中得知自 己的生日时,游戏结束。请问该游戏一共可以进行几轮?
输入格式:
共 $2$ 行。
第 $1$ 行包含1个正整数 $n$ ,表示 $n$ 个人。
第 $2$ 行包含 $n$ 个用空格隔开的正整数 $T_1,T_2,\cdots\cdots,T_n$ ,其中第 $i$ 个整数 $T_i$ 表示编号为 $i$ 的同学的信息传递对象是编号为 $T_i$ 的同学, $T_i \leq n$ 且 $T_i \neq i$ 。
输出格式:
$1$ 个整数,表示游戏一共可以进行多少轮。
样例1解释
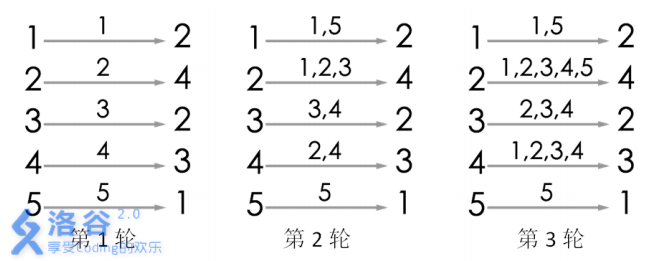
游戏的流程如图所示。当进行完第 $ 3$ 轮游戏后, $4 $ 号玩家会听到 $2$ 号玩家告诉他自己的生日,所以答案为 $3$ 。当然,第 $3$ 轮游戏后, $ 2 $ 号玩家、 $3$ 号玩家都能从自己的消息来源得知自己的生日,同样符合游戏结束的条件。
对于 $30\%$ 的数据, $n ≤ 200$ ;
对于 $60\%$ 的数据, $n ≤ 2500$ ;
对于 $ 100\%$ 的数据, $n ≤ 200000$ 。
仔细读题可以想到,每个人可以看做一个点,每一个传递信息则可以看做一条有向边
那我们画出样例的图
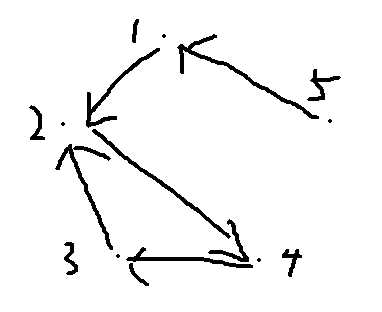
发现了什么?
1.每条边的出度都是1
2.好像,答案等于环的边数?
对1分析,由于每条边的出度都是1,那么整个图只有三种可能1.单链2.单环3.一条单链连一个单环
对2分析,如果一个人可以从别人那里知道自己生日,那么他一定在一个环中,每一次信息传递相当于在环上走一步,所以题目可以转化为求最小环
对1的三种情况分析,第一种情况和第三种情况中的单链都是不合法的情况,考虑删去,之后只要在合法的图上跑一遍dfs求出最小环即可
那怎么删点呢,对于一条单链来说,肯定有一个点是没有入度的
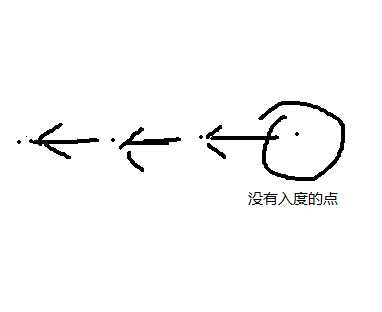
那么我们就删去这个点,然后把它连到的所有点的入度-1,然后继续判断,这样就可以删去所有不合法的点
还不理解的话代码中会有讲解
完整代码
#include<bits/stdc++.h> using namespace std; const int MAXN=200000+10; int n,a[MAXN],r[MAXN],vis[MAXN],ans=999999999;//a存边,r存入度数量,vis标记删点,ans初始化为极大值 void pop(int x)//删点 { vis[x]=1;//标记删除 r[a[x]]--;//它的下家入度-1 if(!r[a[x]]&&!vis[a[x]])pop(a[x]);//判断它的下家是否合法 } void dfs(int qd,int zd,int step) { if(qd==zd&&step)//如果走到了且路程不为0 { ans=min(ans,step);//更新答案 return; } if(!vis[a[qd]])//如果下家合法 { vis[a[qd]]=1;//标记走过,这里并不用回溯,因为都是删完点之后都是单环,没有回溯的必要 dfs(a[qd],zd,step+1);//往下走 } } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); r[a[i]]++; //记录入度数量 } for(int i=1;i<=n;i++)//删点 if(!r[i]&&!vis[i])//没有入度且还没被删 pop(i);//删 for(int i=1;i<=n;i++) { if(!vis[i]) dfs(i,i,0);//一开始起点等于终点 } printf("%d",ans);//输出答案 return 0; }
参考大佬@深海鱼的眼泪的题解
标签:ADG png == copy orange class 更新 不用 回溯
原文地址:https://www.cnblogs.com/pcpcppc/p/9502049.html