标签:技术 type nlogn alt image get tchar bit +=
蝴蝶操作
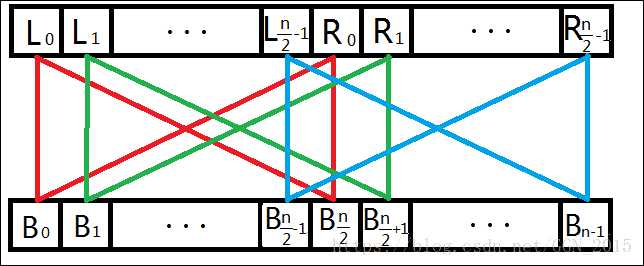

FFT code:
#include<cstdio> #include<cstdlib> #include<cmath> #include<algorithm> #include<cstring> #include<complex> using namespace std; typedef complex<double> cd;//复数类的定义 const int maxl=2094153;//nlogn的最大长度(来自leo学长的博客) const double PI=3.14159265358979;//圆周率,不解释 cd a[maxl],b[maxl];//用于储存变换的中间结果 int rev[maxl];//用于储存二进制反转的结果 void getrev(int bit){ for(int i=0;i<(1<<bit);i++){//高位决定二进制数的大小 rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1)); }//能保证(x>>1)<x,满足递推性质 } void fft(cd* a,int n,int dft){//变换主要过程 for(int i=0;i<n;i++){//按照二进制反转 if(i<rev[i])//保证只把前面的数和后面的数交换,(否则数组会被翻回来) swap(a[i],a[rev[i]]); } for(int step=1;step<n;step<<=1){//枚举步长的一半 cd wn=exp(cd(0,dft*PI/step));//计算单位复根 for(int j=0;j<n;j+=step<<1){//对于每一块 cd wnk(1,0);//!!每一块都是一个独立序列,都是以零次方位为起始的 for(int k=j;k<j+step;k++){//蝴蝶操作处理这一块 cd x=a[k]; cd y=wnk*a[k+step]; a[k]=x+y; a[k+step]=x-y; wnk*=wn;//计算下一次的复根 } } } if(dft==-1){//如果是反变换,则要将序列除以n for(int i=0;i<n;i++) a[i]/=n; } } int output[maxl]; char s1[maxl],s2[maxl]; int main(){ scanf("%s%s",s1,s2);//读入两个数 int l1=strlen(s1),l2=strlen(s2);//就算"次数界" int bit=1,s=2;//s表示分割之前整块的长度 for(bit=1;(1<<bit)<l1+l2-1;bit++){ s<<=1;//找到第一个二的整数次幂使得其可以容纳这两个数的乘积 } for(int i=0;i<l1;i++){//第一个数装入a a[i]=(double)(s1[l1-i-1]-‘0‘); } for(int i=0;i<l2;i++){//第二个数装入b b[i]=(double)(s2[l2-i-1]-‘0‘); } getrev(bit);fft(a,s,1);fft(b,s,1);//dft for(int i=0;i<s;i++)a[i]*=b[i];//对应相乘 fft(a,s,-1);//idft for(int i=0;i<s;i++){//还原成十进制数 output[i]+=(int)(a[i].real()+0.5);//注意精度误差 output[i+1]+=output[i]/10; output[i]%=10; } int i; for(i=l1+l2;!output[i]&&i>=0;i--);//去掉前导零 if(i==-1)printf("0");//特判长度为0的情况 for(;i>=0;i--){//输出这个十进制数 printf("%d",output[i]); } putchar(‘\n‘); return 0; }
NTT(快速数论变换)的多项式乘法的代码:
#include<cstdio> #include<cstdlib> #include<algorithm> #include<cmath> //#include<complex> using namespace std; //typedef complex<double> cd; typedef long long LL; void exgcd(int a,int b,int& x,int& y){ if(b==0){ x=1; y=0; return; } int x0,y0; exgcd(b,a%b,x0,y0); x=y0;y=x0-int(a/b)*y0; } int Inv(int a,int p){ int x,y; exgcd(a,p,x,y); x%=p; while(x<0)x+=p; return x; } int qpow(int a,int b,int p){ if(b<0){ b=-b; a=Inv(a,p); } LL ans=1,mul=a%p; while(b){ if(b&1)ans=ans*mul%p; mul=mul*mul%p; b>>=1; } return ans; } #define maxn (65537*2) const int MOD=479*(1<<21)+1,G=3; int rev[maxn]; void get_rev(int bit){ for(int i=0;i<(1<<bit);i++){ rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1)); } } //from internet //for(int i=0; i<NUM; i++) //{ // int t = 1 << i; // wn[i] = quick_mod(G, (P - 1) / t, P); //} LL a[maxn],b[maxn]; void ntt(LL* a,int n,int dft){ for(int i=0;i<n;i++){ if(i<rev[i]) swap(a[i],a[rev[i]]); } for(int step=1;step<n;step<<=1){ LL wn; wn=qpow(G,dft*(MOD-1)/(step*2),MOD); for(int j=0;j<n;j+=step<<1){ LL wnk=1;//这里一定要用long long不然会迷之溢出 for(int k=j;k<j+step;k++){ LL x=a[k]%MOD,y=(wnk*a[k+step])%MOD;//这里也要用long long a[k]=(x+y)%MOD; a[k+step]=((x-y)%MOD+MOD)%MOD; wnk=(wnk*wn)%MOD; } } } if(dft==-1){ int nI=Inv(n,MOD); for(int i=0;i<n;i++) a[i]=a[i]*nI%MOD; } } #include<cstring> char s1[maxn],s2[maxn]; int main(){ //scanf("%*d"); scanf("%s%s",s1,s2); int l1=strlen(s1),l2=strlen(s2); for(int i=0;i<l1;i++)a[i]=s1[l1-i-1]-‘0‘; for(int i=0;i<l2;i++)b[i]=s2[l2-i-1]-‘0‘; int bit,s=2; for(bit=1;(1<<bit)<(l1+l2-1);bit++)s<<=1; get_rev(bit);ntt(a,s,1);ntt(b,s,1); for(int i=0;i<s;i++) a[i]=a[i]*b[i]%MOD; ntt(a,s,-1); for(int i=0;i<s;i++){ a[i+1]+=a[i]/10; a[i]%=10; } int cnt=s; while(cnt>=0 && a[cnt]==0)cnt--; if(cnt==-1)printf("0"); for(int i=cnt;i>=0;i--){ printf("%d",a[i]); } putchar(‘\n‘); return 0; }
标签:技术 type nlogn alt image get tchar bit +=
原文地址:https://www.cnblogs.com/guxuanqing/p/9502631.html