标签：公式   分享图片   ping   正数   linear   相同   激活   display   测试   

模型训练技巧

神经网络模型设计训练流程

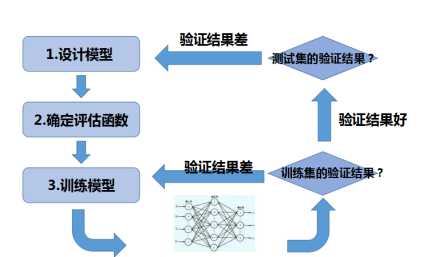
图1-1 神经模型设计流程

  当我们设计并训练好一个神经网络之后，需要在训练集上进行验证模型效果是否良好。这一步的目的在于判断模型是否存在欠拟合；在确定已经在训练集上拟合的很好，就需要在测试集上进行验证，如果验证结果差就需要重新设计模型；如果效果一般，可能需要增加正则化，或者增加训练数据；

欠拟合处理策略

 当模型在训练集上的表现结果并不好的时候，在排除不是数据集和训过程有问题，你可以采用以下几个方法来进行处理。

更换激活函数

Sigmoid激活函数

 Sigmoid函数的形式如（1）所示，图结构如图1-2所示

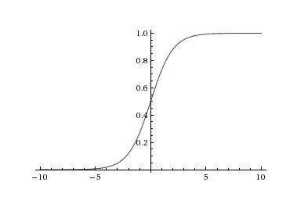
图1-2 sigmoid函数

 但是使用Sigmoid函数作为激活函数会存在梯度消失的现象。就是当神经网络的隐藏层数量超过3层的时候，底层的参数更新就几乎为0；

ReLu（Rectified Linear Unit）激活函数

  ReLu函数的形式如（2）所示，图形结构如图1-3所示

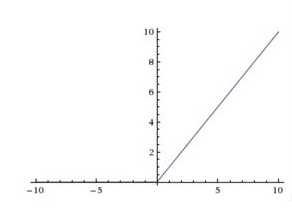
图1-3 ReLu函数

  使用ReLu作为激活函数的原因在于：1）计算更为简单，相比与Sigmoid函数，ReLu计算的更为简单2）ReLu相当于无穷多个不同偏置的Sigmoid函数叠加起来的效果3）ReLu可以解决梯度消失的问题。由于ReLu函数结构，当某个神经元的输出为0时（如图1-4所示），就相当于该神经元在神经网络中不起任何作用，可以将这一些神经元从神经网络中舍去（如图1-5）。

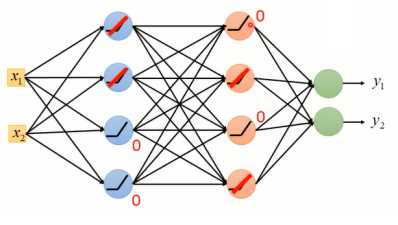
图1-4 神经网络中输出为0的神经元

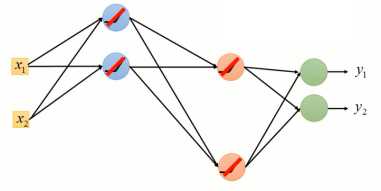
图1-5 “瘦长线性”神经网络

Leaky ReLu激活函数

 由于当ReLu的输入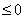时，对应的神经元就不起任何作用。因此，Leaky ReLu的改进点是当输入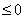时，输出不再是0，而是一个较小值。Leaky ReLu函数结构如（3）所示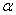，的取值通常需要人工赋值，如当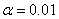时，函数结构如1-6所示

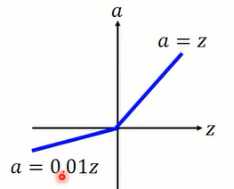
图1-6 Leaky ReLu激活函数

Parametric ReLu激活函数

 由于在Leaky ReLu中的需要人工赋值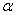，赋值的好坏需要一定的先验知识。因此，Parametric ReLu中的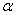是参数，是可以被训练出来，甚至每一个神经元都可以有不同的。

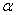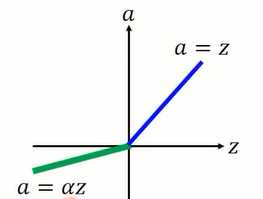
图1-7 Parametric ReLu激活函数

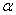  的训练情况更一般参数一样，但跟一般的参数更新有所区别的是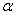采用带有动量的更新方法

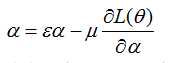
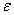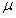  其中为动量，为学习率；

Maxout可学习激活函数（Learnable Activation Function）

  Maxout是一种可学习的激活函数，它可以学习出来ReLu函数的形式。因此，ReLu是Maxout的一种特殊情况。 Maxout结构如图1-8所示，当输出值跟权重相乘后，并不是送进激活函数进行转换，而是将若干元素作为一组（元素数量需预先设定），选择最大值作为输出。

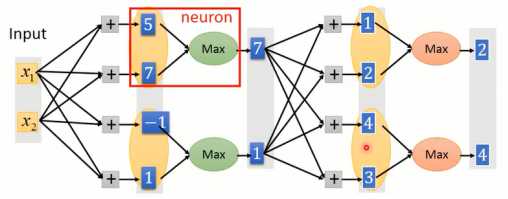
图1-8 Maxout结构

  以图1-9为例，当其中一个输入为1，则最终可以的激活函数实行为图1-10所示。根据你选择多少个元素作为一组，就可以训练出任意的分段函数。

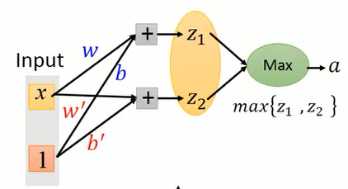
图1-9 Maxout示例

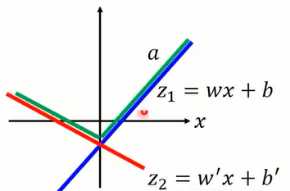
图1-10 Maxout训练出的激活函数

自适应学习率

Adagrad

     Adagrad是将学习率的取值跟之前所有偏微分值的均方值的根号有关系。以当个参数为例，具体的计算如下

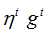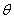  其中，表示对的偏导数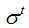；表示将先前所有对参数的偏导数的平方进行累加，并求均值，最后再取根号；

RMSProp

  RMSProp的计算公式如（7）所示，从公式中可以看出，在进行参数更新的时候，不仅考虑了当前的梯度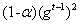，也考虑了先前历史的梯度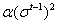。其中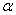是可以自己设置的常数，当的值较小时，就表示比较相信当前的梯度。

Momentum

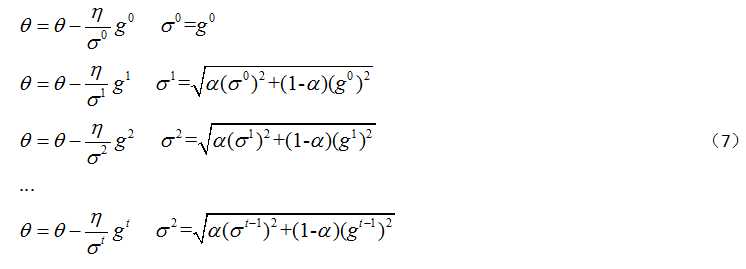
 Momentum的思想来自于现实生活中的场景，当我们往一个崎岖的抛一个球时，由于重力势能，会导致球不一定停留在第一个凹点，可能会翻过第一个凸点，到达全局最低点。

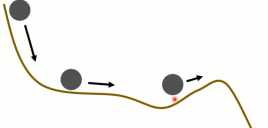
图1-11 Momentum现实场景

 因此，不同于以往的移动方向只考虑梯度方向，也会考虑到以往的移动方向。具体的计算公式中为（8）

过拟合处理策略

早停（Early Stopping）

  早停的思想就是，当模型在训练集上的训练误差在降低时，在测试集的测试误差可能会增加，如图1-12所示。因此需要在训练误差和测试误差之间做一个权衡。

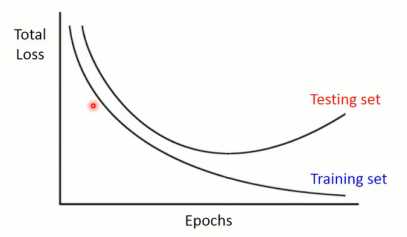
图1-12 训练误差与测试误差

正则化（Regularization）

   添加正则化的目的在于增加模型的平滑性，并且通常会在已有的损失函数上添加一些跟参数相关的项。

L2正则化

   假定现在已经确定的损失函数为L(θ)，而L2正则化会对添加一项，L(θ)形式如（9）

  当添加上L2之后，对于参数的跟新形式变为（10）

  对于（10）的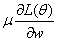跟不添加L2正则项是一样的，而增加L2后，就相当于参数w在更新之前总是会乘上一个小于1的数，因此总是会使w的值减小，这个计算过程称作Weight Decay。L2的效果是使得参数越来越接近0，而我们在初始化参数时通常也会初始化接近于0的值；而我们更新的参数是使得参数越来越远离0,；因此，L2的效果跟早停的效果有些相似。

L1正则化

    L1正则化跟L2正则化非常相似，只是L2是取平方和，而L1是取绝对值，形式如（11）

   添加L1项后，参数的更新形式就为

 因此，当w>0时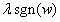，为正，从而使得w的值减小；反之，当w<0时，就会加上一个正数，从而使w的值增加。由于L2是每次都乘上一个小于0的系数因此w减小的会比较明显；而L1是每次都减去一个固定值，因此下降的比较缓慢；所以，在最终训练出来的w，添加L2项的参数普遍较小；添加L1的参数可能有大有小。

Dropout

   Dropout的做法是对于一个确定好的神经网络模型，每一次更新参数前都会对原始模型中的每一个神经元进行采样，决定是否丢弃神经元，每一个神经元都有p%的几率被丢掉。

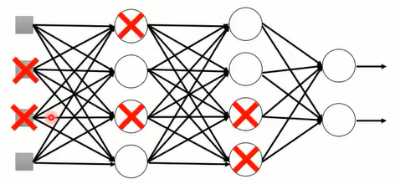
图1-13 dropout采样过程

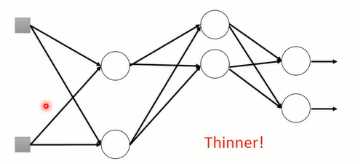
图1-14 dropout采样后的NN结构

     在训练的时候需要对模型进行dropout采样，但是当测试的时候就不要进行采样，而且，每一个参数都要乘上（1-p）%。如图1-15所示，假设dropout几率为50%，则训练时有一半的神经元会被丢弃。而在测试时，为了使测试和训练的输出尽可能相同，就需要对每一个权重都乘上（1-p）%，以保持输出值的平衡（如图1-15右图所示）。

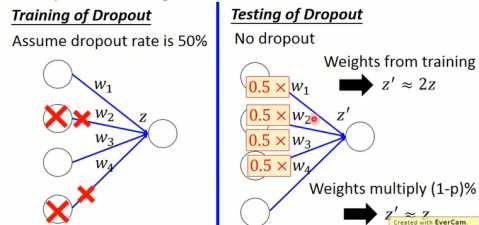
图1-15 dropout测试权重处理

Dropout原理解释

  Dropout可以看做是一种集成学习。集成学习的做法大致是，从训练集中采样出多笔数据，分别去训练不同的模型（模型的结构可以不同）。用训练出的多个模型分别对测试集进行预测，将最终的结果进行平均（如图1-16所示）。

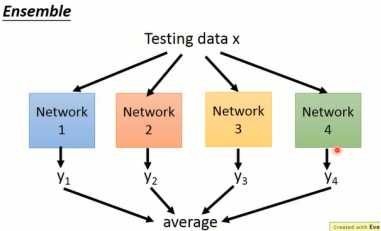
图1-16 集成学习的处理方法

 假定设计的神经网络中的神经元个数为M个，每个神经元可能被dropout或者不被dropout。因此，每个神经元有2种选择，而M个神经元就有2^M选择，对应的就可以产生2^M种模型结构。因此，在训练模型时，就相当于训练了多个模型。对于模型中的某个权重是，在不同的dropout的神经网络中是共享的。

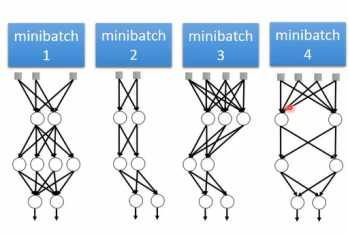
图1-17 dropout训练过程

  但是，在训练好之后，需要进行预测。但是无法将如此多的模型分别进行存储，并单独预测。于是，为了解决这个问题，就在所有的不Dropout的模型的权重都乘上（1-p）%。

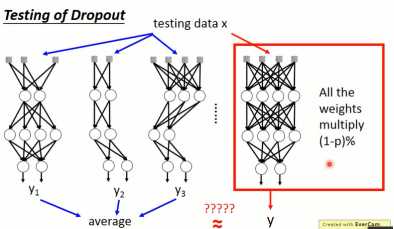
图1-18 dropout权重处理

 Dropout在线性激活函数上的表现会更好。原因在于，当激活函数为线性是，所有权重都乘上（1-p）%，dropout后的模型输出跟集成输出的结果更加接近了。

Sigmoid梯度消失分析

 但是使用Sigmoid函数作为激活函数会存在梯度消失的现象。就是当神经网络的隐藏层数量超过3层的时候，底层的参数更新就几乎为0；这是因为Sigmoid求导公式为S(x)‘=S(x)(1-S(x))，当时x=0,S(x)=0.5时，maxS(x)‘=0.25而当我们要求解底层的参数时，需要累乘上层参数的斜率，也就是要乘上多个小于0.25的数，当乘的个数较多时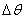，的值就会变得很小，从而导致梯度消失现象。而由于ReLu函数的斜率为1，进行求导在累乘，不会产生上述情况。

参考资料

[1]机器学习-李宏毅

模型训练技巧

标签：公式   分享图片   ping   正数   linear   相同   激活   display   测试   

原文地址：https://www.cnblogs.com/MrPan/p/9503008.html