常用技巧精选（一）

时间：2018-08-20 23:52:27 阅读：402 评论：0 收藏：0 [点我收藏+]

标签：二分搜索分享图片高效 inpu time oss ica down queue

尺取法

Subsequence(POJ 3061)

原题如下：
Subsequence

Time Limit: 1000MS Memory Limit: 65536K

Total Submissions: 20969 Accepted: 8948

Description

A sequence of N positive integers (10 < N < 100 000), each of them less than or equal 10000, and a positive integer S (S < 100 000 000) are given. Write a program to find the minimal length of the subsequence of consecutive elements of the sequence, the sum of which is greater than or equal to S.

Input

The first line is the number of test cases. For each test case the program has to read the numbers N and S, separated by an interval, from the first line. The numbers of the sequence are given in the second line of the test case, separated by intervals. The input will finish with the end of file.

Output

For each the case the program has to print the result on separate line of the output file.if no answer, print 0.

Sample Input
```
2
10 15
5 1 3 5 10 7 4 9 2 8
5 11
1 2 3 4 5
```
Sample Output
```
2
3
```
分析：由于所有的元素大于0，假设存在子序列[s,t)满足a_s+…+a_t-1≥S，那么对于任何的t‘>t一定有a_s+…+a_t‘-1≥S。另外，如果令sum(i)=a₀+a₁+…+a_i-1，那么a_s+a_s+1…+a_t-1=sum(t)-sum(s)，所以预先计算好sum的话，可以用O(1)的时间计算区间上的总和，这样一来，子序列的起点s确定以后，便可以用二分搜索快速确定使序列和不小于S的结尾t的最小值，这个算法的复杂度是O(nlogn)。还有一种更为高效的算法，设以a_s开始总和最初大于S时的连续子序列为a_s+…+a_t-1，这时，a_s+1+…+a_t-2<a_s+…+a_t-2<S，所以从a_s+1开始总和最初超过S的连续子序列如果是a_s+1+…+a_t‘-1的话，必然有t‘≥t。利用这一性质，可设计如下算法：①以s=t=sum=0初始化
②只要依然有sum<S,就不断将sum增加a_t，并将t增加1
③如果②中无法满足sum≥S则终止，否则，更新res=min(res, t-s)
④将sum减去a_s，s增加1然后回到②
对于这个算法，因为s，t只能不断地增大，最多变化n次，因此只需O(n)的复杂度就可以求解这个问题了，像这样反复地推进区间的开头和结尾，来求取满足条件的最小区间的方法被称为尺取法。

代码1：

 1 #include <cstdio>
 2 #include <cctype>
 3 #include <algorithm>
 4 #include <cmath>
 5 #define num s-‘0‘
 6 
 7 using namespace std;
 8 
 9 const int MAX_N=1000000;
10 const int INF=0x3f3f3f3f;
11 int n,S,t;
12 int a[MAX_N],sum[MAX_N+1];
13 
14 int min(int x, int y)
15 {
16     if (x<y) return x;
17     return y;
18 }
19 
20 void read(int &x){
21     char s;
22     x=0;
23     bool flag=0;
24     while(!isdigit(s=getchar()))
25         (s==‘-‘)&&(flag=true);
26     for(x=num;isdigit(s=getchar());x=x*10+num);
27     (flag)&&(x=-x);
28 }
29 
30 void write(int x)
31 {
32     if(x<0)
33     {
34         putchar(‘-‘);
35         x=-x;
36     }
37     if(x>9)
38         write(x/10);
39     putchar(x%10+‘0‘);
40 }
41 
42 int main()
43 {
44     read(t);
45     while (t>0)
46     {
47         read(n);read(S);
48         for (int i=0; i<n; i++) 
49         {
50             read(a[i]);
51             sum[i+1]=sum[i]+a[i];
52         }
53         int res=n+1;
54         for (int s=0; sum[n]-sum[s]>=S; s++)
55         {
56             int t=lower_bound(sum+s,sum+n,sum[s]+S)-sum;
57             res=min(res,t-s);
58         }
59         if (res<=n) write(res);
60         else write(0);
61         putchar(‘\n‘);
62         --t;
63     }
64 }

Subsequence1

代码2：

 1 #include <cstdio>
 2 #include <cctype>
 3 #include <algorithm>
 4 #include <cmath>
 5 #define num s-‘0‘
 6 
 7 using namespace std;
 8 
 9 const int MAX_N=1000000;
10 const int INF=0x3f3f3f3f;
11 int n,S,m;
12 int a[MAX_N];
13 
14 int min(int x, int y)
15 {
16     if (x<y) return x;
17     return y;
18 }
19 
20 void read(int &x){
21     char s;
22     x=0;
23     bool flag=0;
24     while(!isdigit(s=getchar()))
25         (s==‘-‘)&&(flag=true);
26     for(x=num;isdigit(s=getchar());x=x*10+num);
27     (flag)&&(x=-x);
28 }
29 
30 void write(int x)
31 {
32     if(x<0)
33     {
34         putchar(‘-‘);
35         x=-x;
36     }
37     if(x>9)
38         write(x/10);
39     putchar(x%10+‘0‘);
40 }
41 
42 int main()
43 {
44     read(m);
45     while (m>0)
46     {
47         read(n);read(S);
48         for (int i=0; i<n; i++) 
49         {
50             read(a[i]);
51         }
52         int s,t,sum;
53         s=t=sum=0;
54         int res=n+1;
55         for (;;)
56         {
57             while (t<n && sum<S) sum+=a[t++];
58             if (sum<S) break;
59             res = min(res,t-s);
60             sum-=a[s++];
61         }
62         if (res>n) res=0;
63         write(res);
64         putchar(‘\n‘);
65         --m;
66     }
67 }

Subsequence2

Jessica‘s Reading Problem(POJ 3320)

原题如下:
Jessica‘s Reading Problem

Time Limit: 1000MS Memory Limit: 65536K

Total Submissions: 16900 Accepted: 5853

Description

Jessica‘s a very lovely girl wooed by lots of boys. Recently she has a problem. The final exam is coming, yet she has spent little time on it. If she wants to pass it, she has to master all ideas included in a very thick text book. The author of that text book, like other authors, is extremely fussy about the ideas, thus some ideas are covered more than once. Jessica think if she managed to read each idea at least once, she can pass the exam. She decides to read only one contiguous part of the book which contains all ideas covered by the entire book. And of course, the sub-book should be as thin as possible.

A very hard-working boy had manually indexed for her each page of Jessica‘s text-book with what idea each page is about and thus made a big progress for his courtship. Here you come in to save your skin: given the index, help Jessica decide which contiguous part she should read. For convenience, each idea has been coded with an ID, which is a non-negative integer.

Input

The first line of input is an integer P (1 ≤ P ≤ 1000000), which is the number of pages of Jessica‘s text-book. The second line contains P non-negative integers describing what idea each page is about. The first integer is what the first page is about, the second integer is what the second page is about, and so on. You may assume all integers that appear can fit well in the signed 32-bit integer type.

Output

Output one line: the number of pages of the shortest contiguous part of the book which contains all ideals covered in the book.

Sample Input
```
5
1 8 8 8 1
```
Sample Output
```
2
```
题解：假设从某一页s开始阅读，为了覆盖所有的知识点需要阅读到t，如果从s+1开始阅读的话，必须阅读到t‘≥t页为止，因此，这题可以使用尺取法。这题的关键是，在某个区间[s,t]已经覆盖了所有的知识点的情况下，下一个区间[s+1,t‘](t‘≥t)要如何求出？有这样一个等价关系：所有的知识点都被覆盖?每个知识点出现的次数都不小于1，由这个等价关系，我们可以用二叉树等数据结构来存储[s,t]区间上每个知识点的出现次数，这样把最开头的页s去除后便可以判断[s+1,t]是否满足条件，从区间的开头把s取出后，页s上书写的知识点的出现次数就要减一，如果此时这个知识点的出现次数为0了，在同一个知识点再次出现前，不停将区间末尾t向后推进即可，每次在区间末尾追加页t时将页t上的知识点的出现次数加1，这样就完成了下一个区间上各个知识点出现次数的更新，通过重复这一操作可以以O(PlogP)的复杂度内求出最小的区间了

代码：

 1 #include <cstdio>
 2 #include <cctype>
 3 #include <algorithm>
 4 #include <cmath>
 5 #include <map>
 6 #include <set>
 7 #define num s-‘0‘
 8 
 9 using namespace std;
10 
11 const int MAX_N=1000000;
12 const int INF=0x3f3f3f3f;
13 int P;
14 int a[MAX_N];
15 
16 int min(int x, int y)
17 {
18     if (x<y) return x;
19     return y;
20 }
21 
22 void read(int &x){
23     char s;
24     x=0;
25     bool flag=0;
26     while(!isdigit(s=getchar()))
27         (s==‘-‘)&&(flag=true);
28     for(x=num;isdigit(s=getchar());x=x*10+num);
29     (flag)&&(x=-x);
30 }
31 
32 void write(int x)
33 {
34     if(x<0)
35     {
36         putchar(‘-‘);
37         x=-x;
38     }
39     if(x>9)
40         write(x/10);
41     putchar(x%10+‘0‘);
42 }
43 
44 int main()
45 {
46     read(P);
47     set<int> all;
48     for (int i=0; i<P; i++)
49     {
50         read(a[i]);
51         all.insert(a[i]);
52     }
53     int n=all.size();
54     int s=0, t=0, numb=0;
55     map<int, int> count;
56     int res = P;
57     for (;;)
58     {
59         while (t<P && numb<n)
60             if (count[a[t++]]++==0) numb++;
61         if (numb<n) break;
62         res=min(res,t-s);
63         if (--count[a[s++]]==0) numb--;
64     }
65     write(res);
66 }

Jessica‘s Reading Problem

反转（开关问题）

Face The Right Way(POJ 3276)

原题如下：
Face The Right Way

Time Limit: 2000MS Memory Limit: 65536K

Total Submissions: 6704 Accepted: 3121

Description

Farmer John has arranged his N (1 ≤ N ≤ 5,000) cows in a row and many of them are facing forward, like good cows. Some of them are facing backward, though, and he needs them all to face forward to make his life perfect.

Fortunately, FJ recently bought an automatic cow turning machine. Since he purchased the discount model, it must be irrevocably preset to turn K (1 ≤ K ≤ N) cows at once, and it can only turn cows that are all standing next to each other in line. Each time the machine is used, it reverses the facing direction of a contiguous group of K cows in the line (one cannot use it on fewer than K cows, e.g., at the either end of the line of cows). Each cow remains in the same *location* as before, but ends up facing the *opposite direction*. A cow that starts out facing forward will be turned backward by the machine and vice-versa.

Because FJ must pick a single, never-changing value of K, please help him determine the minimum value of K that minimizes the number of operations required by the machine to make all the cows face forward. Also determine M, the minimum number of machine operations required to get all the cows facing forward using that value of K.

Input

Line 1: A single integer: N
Lines 2..N+1: Line i+1 contains a single character, F or B, indicating whether cow i is facing forward or backward.

Output

Line 1: Two space-separated integers: K and M

Sample Input
```
7
B
B
F
B
F
B
B
```
Sample Output
```
3 3
```
Hint

For K = 3, the machine must be operated three times: turn cows (1,2,3), (3,4,5), and finally (5,6,7)
分析：对于一个特定的K如何求出让所有的牛面朝前方的最小操作次数？首先，交换区间反转的顺序对结果是没有影响的，另外，可以知道对同一个区间进行两次以上的反转是多余的，由此，问题就转化成了求需要反转的区间的集合。先考虑一下最左端的牛，因为包含这头牛的区间只有一个，所以如果这头牛面朝前方，我们就能知道这个区间不需要反转，反之如果这头牛面朝后方，对应的区间就必须进行反转了，而且在此之后的最左区间就再也不需要考虑了，这样一来通过首先考虑最左端的牛，问题的规模就缩小了1，不断地重复下去，就可以无需搜索求出最少所需反转次数了。通过前面的分析可以知道，忽略掉对同一个区间重复反转这类多余操作之后，只要存在让所有的牛都朝前的方法，那么操作就和顺序无关，可以唯一确定了。对于整个算法的话，我们需要对所有的K都求解一次，对于每个K最坏情况下需要进行N-K+1次的反转操作，每次操作又要反转K头牛，于是总的复杂度是O(N³)。区间反转的部分还可以进行优化，令f[i]:=区间[i,i+K-1]进行了反转的话为1，否则为0，这样在考虑第i头牛时，如果∑（j=i-K+1,i-1）f[j]为奇数的话，则这头牛的方向与起始方向是相反的，否则方向不变，由于∑（j=(i+1)-K+1,i）f[j] = ∑（j=i-K+1,i-1）f[j]+f[i]-f[i-K+1]，所以这个和每一次都可以用常数时间计算出来，复杂度就降为了O(N²)，就可以在时限内解决问题了。

代码：

 1 #include <cstdio>
 2 #include <cctype>
 3 #include <algorithm>
 4 #include <cmath>
 5 #include <cstring>
 6 #define num s-‘0‘
 7 
 8 using namespace std;
 9 
10 const int MAX_N=5001;
11 const int INF=0x3f3f3f3f;
12 int N;
13 int dir[MAX_N], f[MAX_N];
14 
15 void read(int &x){
16     char s;
17     x=0;
18     bool flag=0;
19     while(!isdigit(s=getchar()))
20         (s==‘-‘)&&(flag=true);
21     for(x=num;isdigit(s=getchar());x=x*10+num);
22     (flag)&&(x=-x);
23 }
24 
25 void write(int x)
26 {
27     if(x<0)
28     {
29         putchar(‘-‘);
30         x=-x;
31     }
32     if(x>9)
33         write(x/10);
34     putchar(x%10+‘0‘);
35 }
36 
37 int calc(int);
38 
39 int main()
40 {
41     read(N);
42     for (int i=0; i<N; i++)
43     {
44         char d;
45         scanf("%c", &d);
46         d==‘B‘? dir[i]=1: dir[i]=0;
47         scanf("%c", &d);
48     }
49     int K=1,M=N;
50     for (int k=N; k>=1; k--)
51     {
52         int m=calc(k);
53         if (m>=0 && m<M)
54         {
55             M=m;
56             K=k;
57         }
58     }
59     write(K);putchar(‘ ‘);write(M);putchar(‘\n‘);
60 }
61 
62 int calc(int K)
63 {
64     memset(f, 0, sizeof(f));
65     int res=0;
66     int sum=0;
67     for (int i=0; i<=N-K; i++)
68     {
69         if ((dir[i]+sum)%2 != 0)
70         {
71             res++;
72             f[i]=1;
73         }
74         sum+=f[i];
75         if (i-K+1>=0) sum-=f[i-K+1];
76     }
77     for (int i=N-K+1; i<N; i++)
78     {
79         if ((dir[i]+sum)%2!=0) return -1;
80         if (i-K+1>=0) sum-=f[i-K+1];
81     }
82     return res;
83 }

Face The Right Way

Fliptile(POJ 3279)

原题如下:
Fliptile

Time Limit: 2000MS Memory Limit: 65536K

Total Submissions: 16480 Accepted: 6016

Description

Farmer John knows that an intellectually satisfied cow is a happy cow who will give more milk. He has arranged a brainy activity for cows in which they manipulate an M × N grid (1 ≤ M ≤ 15; 1 ≤ N ≤ 15) of square tiles, each of which is colored black on one side and white on the other side.

As one would guess, when a single white tile is flipped, it changes to black; when a single black tile is flipped, it changes to white. The cows are rewarded when they flip the tiles so that each tile has the white side face up. However, the cows have rather large hooves and when they try to flip a certain tile, they also flip all the adjacent tiles (tiles that share a full edge with the flipped tile). Since the flips are tiring, the cows want to minimize the number of flips they have to make.

Help the cows determine the minimum number of flips required, and the locations to flip to achieve that minimum. If there are multiple ways to achieve the task with the minimum amount of flips, return the one with the least lexicographical ordering in the output when considered as a string. If the task is impossible, print one line with the word "IMPOSSIBLE".

Input

Line 1: Two space-separated integers: M and N
Lines 2..M+1: Line i+1 describes the colors (left to right) of row i of the grid with N space-separated integers which are 1 for black and 0 for white

Output

Lines 1..M: Each line contains N space-separated integers, each specifying how many times to flip that particular location.

Sample Input
```
4 4
1 0 0 1
0 1 1 0
0 1 1 0
1 0 0 1
```
Sample Output
```
0 0 0 0
1 0 0 1
1 0 0 1
0 0 0 0
```
分析：首先，同一个格子翻转两次的话就会恢复原状，所以多次反转是多余的，此外，翻转的格子的集合相同的话，其次序是无关紧要的，所以总共有2^MN种翻转的方法，由于解空间实在太大，我们必须另寻他径，参考解决POJ3276的方法，那道题中，让最左端的牛反转的方法只有1种，所以只要用直接判断的方法确定就可以了，但在这里，是行不通的，比如左上角的格子，除了翻转(1,1)之外，翻转(1,2)和(2,1)也都可以把(1,1)翻转，所以不能直接套用POJ3276的方法，但是如果假设第一行的翻转方法已经确定，那么翻转(1,1)的就只剩下(2,1)了，所以可以直接判断(2,1)是否需要翻转，类似的第二行都可以判断，如此反复下去就可以判断出所有格子的翻转方法了，判断是否有解，只要看最后一行是不是全为白色即可，如果并非全白，那么就说明不存在可行的操作方法。综上，我们只要先确定出第一行的翻转方式即可，而第一行的翻转方式共有2^N种，所以总的时间复杂度为O(MN2^N)

代码：

  1 #include <cstdio>
  2 #include <cctype>
  3 #include <algorithm>
  4 #include <cmath>
  5 #include <cstring>
  6 #define number s-‘0‘
  7 
  8 using namespace std;
  9 
 10 const int MAX_N=16;
 11 const int INF=0x3f3f3f3f;
 12 const int dx[5]={-1, 0, 0, 0, 1};
 13 const int dy[5]={0, 1, 0, -1, 0};
 14 int N,M;
 15 int flip[MAX_N][MAX_N], tile[MAX_N][MAX_N], opt[MAX_N][MAX_N];
 16 
 17 void read(int &x){
 18     char s;
 19     x=0;
 20     bool flag=0;
 21     while(!isdigit(s=getchar()))
 22         (s==‘-‘)&&(flag=true);
 23     for(x=number;isdigit(s=getchar());x=x*10+number);
 24     (flag)&&(x=-x);
 25 }
 26 
 27 void write(int x)
 28 {
 29     if(x<0)
 30     {
 31         putchar(‘-‘);
 32         x=-x;
 33     }
 34     if(x>9)
 35         write(x/10);
 36     putchar(x%10+‘0‘);
 37 }
 38 
 39 int calc();
 40 int get(int, int);
 41 
 42 int main()
 43 {
 44     read(M);read(N);
 45     for (int i=0; i<M; i++)
 46         for (int j=0; j<N; j++)
 47             read(j[i[tile]]);
 48     int res=-1;
 49     for (int i=0; i< 1<<N; i++)
 50     {
 51         memset(flip, 0, sizeof(flip));
 52         for (int j=0; j<N; j++)
 53         {
 54             flip[0][N-j-1]=i>>j&1;
 55         }
 56         int num=calc();
 57         if (num>=0 && (res<0 || num<res))
 58         {
 59             res=num;
 60             memcpy(opt, flip, sizeof(flip));
 61         }
 62     }
 63     if (res<0) puts("IMPOSSIBLE\n");
 64     else
 65         for (int i=0; i<M; i++)
 66             for (int j=0; j<N; j++)
 67                 printf("%d%c", j[i[opt]], j+1==N? ‘\n‘: ‘ ‘);
 68 }
 69 
 70 int get(int x, int y)
 71 {
 72     int c=tile[x][y];
 73     for (int i=0; i<5; i++)
 74     {
 75         int x2=x+dx[i], y2=y+dy[i];
 76         if (0<=x2 && x2<M && 0<=y2 && y2<N)
 77         {
 78             c+=y2[x2[flip]];
 79         }
 80     }
 81     return c % 2;
 82 }
 83 
 84 int calc()
 85 {
 86     for (int i=1; i<M; i++)
 87     {
 88         for (int j=0; j<N; j++)
 89         {
 90             if (get(i-1,j)!=0) flip[i][j]=1;
 91         }
 92     }
 93     for (int j=0; j<N; j++)
 94     {
 95         if (get(M-1,j)!=0) return -1;
 96     }
 97     int res=0;
 98     for (int i=0; i<M; i++)
 99         for (int j=0; j<N; j++)
100             res+=j[i[flip]];
101     return res;
102 }

Fliptile

PS: 在上面的代码里，为了尝试第一行的所有可能性，使用了集合的整数表示，集合{0,1,…,n-1}的子集S可以编码成整数：f(S)=∑2ⁱ，像这样表示之后，一些集合运算可以对应地写成如下方式：

①空集?：……………………………………………0

②只含有1个元素i的集合{i}…………………………1<<i

③含有全部n个元素的集合…………………………(1<<n)-1

④判断第i+1个元素i是否属于集合S………………if (S>>i&1)

⑤向集合中加入第i+1个元素i（S∪{i}）…………S|1<<i

⑥从集合中取出第i+1个元素（S\{i}）……………S&~(1<<i)

⑦集合S和集合T的并集S∪T………………………S|T

⑧集合S和集合T的交集S∩T………………………S&T
此外，想要将集合{0,1,…,n-1}的所有自己枚举出来的话，可以这样写：
```
for (int S=0; S<1<<n; S++)
{
    //对子集的处理
}
```
接下来，介绍如何枚举某个集合sup的子集。这里sup是一个二进制码。
```
(sub-1) & sup
```
(sub-1)&sup会忽略sup中的0而从sub中减去"1"，最终sub可以将sup所有的子集按照降序生成出来。为什么不能用加？因为(sub+1)&sup虽然是sup的子集，但很可能依旧是sub，没有任何改变，而用减就不会出现这样的情况。
```
int sub=sup;
do
{
  //对子集进行处理  
  sub=(sub-1)&sup;
} while (sub != sup);//处理完0之后，会有-1&sup=sup
```
最后，介绍如何枚举{0,1,…,n-1}所包含的所有大小为k的子集。通过位运算，按照字典序升序地枚举出所有满足条件地二进制码，先上代码：
```
int comb = (1<<k)-1;
while (comb< 1<<n)
{
    //这里进行针对组合的处理
    int x=comb&(-comb), y=comb+x;
    comb=((comb&~y)/x>>1)|y;
}
```
按照字典序的话，最小的子集是(1<<k)-1,所有用它作为初始值，下面就要求出comb之后一个二进制码了，方法如下：
①求出最低位的1开始的连续的1的区间（0101110→0001110）
②将这一区间全部变为0，并将区间左侧的那个0变为1（0101110→0110000）
③将第①步里取出的区间右移，直到剩下的1的个数减少了1个（0001110→0000011）
④将第②步和第③步的结果按位取或（0110000|0000011→0110011）
对于非零的整数，x&(-x)的值就是将其最低位的1独立出来的值，即lowbit

除上述例子外，还可以利用位运算完成满足其它条件的集合的枚举，例如不包含相邻元素的集合等

弹性碰撞
Physics Experiment(POJ 3684)

原题如下：
Physics Experiment

Time Limit: 1000MS Memory Limit: 65536K

Total Submissions: 3582 Accepted: 1274 Special Judge

Description

Simon is doing a physics experiment with N identical balls with the same radius of R centimeters. Before the experiment, all N balls are fastened within a vertical tube one by one and the lowest point of the lowest ball is H meters above the ground. At beginning of the experiment, (at second 0), the first ball is released and falls down due to the gravity. After that, the balls are released one by one in every second until all balls have been released. When a ball hits the ground, it will bounce back with the same speed as it hits the ground. When two balls hit each other, they with exchange their velocities (both speed and direction).

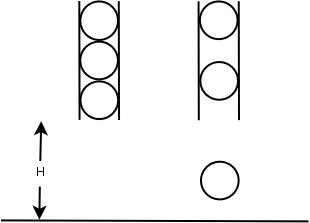
Simon wants to know where are the N balls after T seconds. Can you help him?

In this problem, you can assume that the gravity is constant: g = 10 m/s².

Input

The first line of the input contains one integer C (C ≤ 20) indicating the number of test cases. Each of the following lines contains four integers N, H, R, T.
1≤ N ≤ 100.
1≤ H ≤ 10000
1≤ R ≤ 100
1≤ T ≤ 10000

Output

For each test case, your program should output N real numbers indicating the height in meters of the lowest point of each ball separated by a single space in a single line. Each number should be rounded to 2 digit after the decimal point.

Sample Input
```
2
1 10 10 100
2 10 10 100
```
Sample Output
```
4.95
4.95 10.20
```
分析：一个球的情形很简单。多个球的情形先考虑R=0，模仿热身题(POJ 1852)，在那道题中两只蚂蚁相遇后折返我们将其看作不折返而是擦身而过继续走下去，这里我们就可以无视碰撞，视为直接互相穿过继续运动，由于在有碰撞时，球的相对顺序是不会变得的，所以忽略碰撞，将计算得到的坐标进行排序后，就能直到每个球的最终位置。然后我们再考虑R>0的情形，对于从下方开始的第i个球，在按照R=0计算的结果上加上2Ri就好了。

代码：

 1 #include <cstdio>
 2 #include <cctype>
 3 #include <algorithm>
 4 #include <cmath>
 5 #include <cstring>
 6 #define number s-‘0‘
 7 
 8 using namespace std;
 9 
10 const int MAX_N=110;
11 const double g=10.0;
12 int K,N,H,R,T;
13 double y[MAX_N];
14 
15 void read(int &x){
16     char s;
17     x=0;
18     bool flag=0;
19     while(!isdigit(s=getchar()))
20         (s==‘-‘)&&(flag=true);
21     for(x=number;isdigit(s=getchar());x=x*10+number);
22     (flag)&&(x=-x);
23 }
24 
25 void write(int x)
26 {
27     if(x<0)
28     {
29         putchar(‘-‘);
30         x=-x;
31     }
32     if(x>9)
33         write(x/10);
34     putchar(x%10+‘0‘);
35 }
36 
37 double calc(int);
38 
39 int main()
40 {
41     read(K);
42     while (K>0)
43     {
44         read(N);read(H);read(R);read(T);
45         for (int i=0; i<N; i++)
46         {
47             y[i]=calc(T-i);
48         }
49         sort(y,y+N);
50         for (int i=0; i<N; i++)
51             printf("%.2f%c", y[i]+2*R*i/100.0, i+1==N? ‘\n‘: ‘ ‘);
52         K--;
53     }
54 }
55 
56 double calc(int T)
57 {
58     if (T<=0) return H;
59     double t=sqrt(2*H/g);
60     int k=(int)(T/t);
61     if (k%2==0) 
62     {
63         double d=T-k*t;
64         return H-g*d*d/2;
65     }
66     else
67     {
68         double d=k*t+t-T;
69         return H-g*d*d/2;
70     }
71 }

Physics Experiment

折半枚举（双向搜索）

4 Values whose Sum is 0(POJ 2785)

原题如下：
4 Values whose Sum is 0

Time Limit: 15000MS Memory Limit: 228000K

Total Submissions: 29242 Accepted: 8886

Case Time Limit: 5000MS

Description

The SUM problem can be formulated as follows: given four lists A, B, C, D of integer values, compute how many quadruplet (a, b, c, d ) ∈ A x B x C x D are such that a + b + c + d = 0 . In the following, we assume that all lists have the same size n .

Input

The first line of the input file contains the size of the lists n (this value can be as large as 4000). We then have n lines containing four integer values (with absolute value as large as 2²⁸ ) that belong respectively to A, B, C and D .

Output

For each input file, your program has to write the number quadruplets whose sum is zero.

Sample Input
```
6
-45 22 42 -16
-41 -27 56 30
-36 53 -37 77
-36 30 -75 -46
26 -38 -10 62
-32 -54 -6 45
```
Sample Output
```
5
```
Hint

Sample Explanation: Indeed, the sum of the five following quadruplets is zero: (-45, -27, 42, 30), (26, 30, -10, -46), (-32, 22, 56, -46),(-32, 30, -75, 77), (-32, -54, 56, 30).
分析：从4个数列中选择的话共有n⁴种情况，如果全都判断一遍肯定不可行，但如果将它们对半分成AB和CD再考虑，就可以快速解决了。从2个数列种选择的话只有n²种组合，所以可以进行枚举，先从A,B中取出a，b后，为了使总和为0则需要从C,D中取出c+d=-a-b，因此先将从C,D中取出数字的n²种方法全都枚举出来，将这些和排好序，这样就可以二分搜索了，复杂度O(n²logn).

代码：

 1 #include <cstdio>
 2 #include <cctype>
 3 #include <algorithm>
 4 #include <cmath>
 5 #include <cstring>
 6 #define number s-‘0‘
 7 
 8 using namespace std;
 9 
10 const int MAX_N=5000;
11 int A[MAX_N], B[MAX_N], C[MAX_N], D[MAX_N];
12 int CD[MAX_N*MAX_N];
13 int N;
14 
15 void read(int &x){
16     char s;
17     x=0;
18     bool flag=0;
19     while(!isdigit(s=getchar()))
20         (s==‘-‘)&&(flag=true);
21     for(x=number;isdigit(s=getchar());x=x*10+number);
22     (flag)&&(x=-x);
23 }
24 
25 void write(int x)
26 {
27     if(x<0)
28     {
29         putchar(‘-‘);
30         x=-x;
31     }
32     if(x>9)
33         write(x/10);
34     putchar(x%10+‘0‘);
35 }
36 
37 double calc(int);
38 
39 int main()
40 {
41     read(N);
42     for (int i=0; i<N; i++)
43     {
44            read(A[i]);read(B[i]);read(C[i]);read(D[i]);
45     }
46     for (int i=0; i<N; i++)
47         for (int j=0; j<N; j++)
48             CD[i*N+j]=C[i]+D[j];
49     sort(CD,CD+N*N);
50     long long res=0;
51     for (int i=0; i<N; i++)
52         for (int j=0; j<N; j++)
53         {
54             int cd=-(A[i]+B[j]);
55             res+=upper_bound(CD, CD+N*N, cd)-lower_bound(CD, CD+N*N, cd);
56         }
57     printf("%d\n", res);
58 }

4 Values whose Sum is 0

超大背包问题

问题描述：有重量和价值分别为w_i，v_i的n个物品，从这些物品中挑选总重量不超过W的物品，求所有挑选方案中，价值总和的最大值。
限制条件：
1≤n≤40
1≤w_i，v_i≤10¹⁵
1≤W≤10¹⁵
分析：如果用DP的话，复杂度是O(nW)，这里W数值非常大，所以不能用DP。挑选物品的方法总共有2ⁿ种，不能直接枚举，但可以像之前一样折半枚举，每部分20个是可行的，利用拆成两半后的两部分的价值和重量，可以求出原问题的解，我们把前半部分中的选取方法对应的重量和价值总和记为w1，v1，这样在后半部分寻找总重w2≤W-w1时使v2最大的选取方法就好了。接下来只要思考从枚举得到的(w2,v2)的集合中高效寻找max{v2|w2≤W‘}的方法，首先，先排除所有w2[j]≥w2[i]而v2[j]≤v2[i]的所有j，这一点可以按照w2、v2的字典序排序后简单做到，此后剩余的元素都满足w2[i]<v2[j]?v2[i]<v2[j]，要计算max{v2|w2<W‘}的话，只要寻找满足w2[i]≤W‘的最大的i就可以了，这可以用二分来完成，剩余的元素个数为M的话，一次搜索需要O(logM)的时间，而M<2^(n/2)，所以总的时间复杂度是O(2^(n/2)n)。

代码：

 1 #include <cstdio>
 2 #include <cctype>
 3 #include <algorithm>
 4 #include <cmath>
 5 #include <cstring>
 6 #include <utility>
 7 #define number s-‘0‘
 8 
 9 using namespace std;
10 
11 const int MAX_N=50;
12 const long long INF=0x3fffffffffffffff;
13 int n;
14 long long w[MAX_N], v[MAX_N];
15 long long W;
16 pair<long long, long long> ps[1<<(MAX_N/2)];
17 
18 void read(int &x){
19     char s;
20     x=0;
21     bool flag=0;
22     while(!isdigit(s=getchar()))
23         (s==‘-‘)&&(flag=true);
24     for(x=number;isdigit(s=getchar());x=x*10+number);
25     (flag)&&(x=-x);
26 }
27 
28 void write(int x)
29 {
30     if(x<0)
31     {
32         putchar(‘-‘);
33         x=-x;
34     }
35     if(x>9)
36         write(x/10);
37     putchar(x%10+‘0‘);
38 }
39 
40 long long max(long long x, long long y)
41 {
42     if (x>y) return x;
43     return y; 
44 }
45 
46 int main()
47 {
48     read(n);scanf("%I64d",&W);
49     for (int i=0; i<n; i++)
50     {
51         scanf("%I64d %I64d",&w[i], &v[i]);
52     }
53     int n2=n/2;
54     for (int i=0; i<1<<n2; i++)
55     {
56         long long sw=0, sv=0;
57         for (int j=0; j<n2; j++)
58         {
59             if (i>>j&1)
60             {
61                 sw+=w[j];
62                 sv+=v[j]; 
63             }
64         }
65         ps[i]=make_pair(sw, sv);
66     }
67     sort(ps, ps+(1<<n2));
68     int m=1;
69     for (int i=1; i<1<<n2; i++)
70     {
71         if (ps[m-1].second<ps[i].second)
72         {
73             ps[m++]=ps[i];
74         }
75     }
76     long long res=0;
77     for (int i=0; i<1<<(n-n2); i++)
78     {
79         long long sw=0, sv=0;
80         for (int j=0; j<n-n2; j++)
81         {
82             if (i>>j&1)
83             {
84                 sw+=w[n2+j];
85                 sv+=v[n2+j];
86             }
87         }
88         if (sw<=W)
89         {
90             long long tv=(lower_bound(ps, ps+m, make_pair(W-sw,INF))-1)->second;
91             res=max(res,sv+tv);
92         }
93     }
94     printf("%d\n", res);
95 }

超大背包问题

坐标离散化

问题描述： w*h的格子上画了n条或垂直或水平的宽度为1的直线，求这些直线将格子划分成了多少个区域。
限制条件：
1≤w，h≤1000000
1≤n≤500
分析：这题的关键在于我们没法创建w*h的数组，因为太大了，所以要进行坐标离散化，数组里只需要存储有直线的行列以及其前后的行列就足够了，这样的话6n*6n的空间就可以了。

代码：

  1 #include <cstdio>
  2 #include <cctype>
  3 #include <algorithm>
  4 #include <cmath>
  5 #include <cstring>
  6 #include <vector>
  7 #include <queue>
  8 #include <utility>
  9 #define number s-‘0‘
 10 
 11 using namespace std;
 12 
 13 const int MAX_N=600;
 14 const long long INF=0x3f3f3f3f;
 15 const int dx[4]{-1,0,0,1};
 16 const int dy[4]{0,1,-1,0};
 17 int N,H,W;
 18 int X1[MAX_N],X2[MAX_N],Y1[MAX_N],Y2[MAX_N];
 19 bool fld[MAX_N*6][MAX_N*6];
 20 
 21 void read(int &x){
 22     char s;
 23     x=0;
 24     bool flag=0;
 25     while(!isdigit(s=getchar()))
 26         (s==‘-‘)&&(flag=true);
 27     for(x=number;isdigit(s=getchar());x=x*10+number);
 28     (flag)&&(x=-x);
 29 }
 30 
 31 void write(int x)
 32 {
 33     if(x<0)
 34     {
 35         putchar(‘-‘);
 36         x=-x;
 37     }
 38     if(x>9)
 39         write(x/10);
 40     putchar(x%10+‘0‘);
 41 }
 42 
 43 int compress(int *x1, int *x2, int w);
 44 
 45 int main()
 46 {
 47     read(W);read(H);read(N);
 48     for (int i=0; i<N; i++)
 49     {
 50         read(X1[i]);read(Y1[i]);
 51         read(X2[i]);read(Y2[i]);
 52     }
 53     W=compress(X1, X2, W);
 54     H=compress(Y1, Y2, H);
 55     memset(fld, 0, sizeof(fld));
 56     for (int i=0; i<N; i++)
 57         for (int y=Y1[i]; y<=Y2[i]; y++)
 58             for (int x=X1[i]; x<=X2[i]; x++)
 59                 fld[y][x]=true;
 60     int ans=0;
 61     for (int y=0; y<H; y++)
 62     {
 63         for (int x=0; x<W; x++)
 64         {
 65             if (fld[x][y]) continue;
 66             ans++;
 67             queue<pair<int, int>> que;
 68             que.push(make_pair(x,y));
 69             while (!que.empty())
 70             {
 71                 int sx=que.front().first, sy=que.front().second;
 72                 que.pop();
 73                 for (int i=0; i<4; i++)
 74                 {
 75                     int tx=sx+dx[i], ty=sy+dy[i];
 76                     if (tx<0 || tx>=W || ty<0 || ty>=H) continue;
 77                     if (fld[tx][ty]) continue;
 78                     que.push(make_pair(tx,ty));
 79                     fld[tx][ty]=true;
 80                 }
 81             }
 82         }
 83     }
 84     write(ans);
 85     putchar(‘\n‘);
 86 }
 87 
 88 int compress(int *x1, int *x2, int w)
 89 {
 90     vector<int> xs;
 91     for (int i=0; i<N; i++)
 92     {
 93         for (int d=-1; d<=1; d++)
 94         {
 95             int tx1=x1[i]+d, tx2=x2[i]+d;
 96             if (1<=tx1 && tx1<=w) xs.push_back(tx1);
 97             if (1<=tx2 && tx2<=w) xs.push_back(tx2);
 98         }
 99     }
100     sort(xs.begin(),xs.end());
101     xs.erase(unique(xs.begin(),xs.end()),xs.end());
102     for (int i=0; i<N; i++)
103     {
104         x1[i]=find(xs.begin(), xs.end(), x1[i])-xs.begin();
105         x2[i]=find(xs.begin(), xs.end(), x2[i])-xs.begin();
106     }
107     return xs.size();
108 }

坐标离散化

常用技巧精选（一）

标签：二分搜索分享图片高效 inpu time oss ica down queue

原文地址：https://www.cnblogs.com/Ymir-TaoMee/p/9496710.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行

Time Limit: 1000MS	Memory Limit: 65536K
Total Submissions: 20969	Accepted: 8948

Time Limit: 1000MS	Memory Limit: 65536K
Total Submissions: 16900	Accepted: 5853

Time Limit: 2000MS	Memory Limit: 65536K
Total Submissions: 6704	Accepted: 3121

Time Limit: 2000MS	Memory Limit: 65536K
Total Submissions: 16480	Accepted: 6016

Time Limit: 1000MS	Memory Limit: 65536K
Total Submissions: 3582	Accepted: 1274	Special Judge

Time Limit: 15000MS	Memory Limit: 228000K
Total Submissions: 29242	Accepted: 8886
Case Time Limit: 5000MS