标签:哪些 应该 完全 使用 事件 视频、 test 简单的 技术
机器学习算法被认为是一种从数据中学习的算法。所谓“学习”有一个定义:‘‘对于某类任务 T 和性能度量 P,一个计算机程序被认为可以从经验 E 中学习是指,通过经验 E 改进后,它在任务 T 上由性能度量 P 衡量的性能有所提升。” 下面将对任务、性能度量和经验进行介绍。
从“任务”的相对定义来讲,学习过程不能算成任务,学习能获取一种能力,这种能力可以让我们完成任务。比如我们要让机器人行走,那么行走就是任务。
从机器学习的角度来讲,任务定义为机器学习系统应该如何处理样本(example)。样本是指机器学习系统处理的对象或者从事件中收集到的已经量化的特征(feature)集合。我们通常会将样本表示成一个向量\(x∈\mathbb{R}^n\),其中的每一个元素\(x_i\)被称为一个特征。比如我们要处理的样本为学生数据,每个学生样本可以组成一个向量\(x=[180,75]\),学生样本有两个特征:身高和体重。
机器学习可以解决很多类型的任务。一些常见的任务如下:
在分类任务中,计算机需要指出输入数据属于 k 类中的哪一类。为了完成这类任务,学习算法会返回一个函数(模型)\(f :\mathbb{R}^n→\{1,2,...,k\}\)。当输入一个n维向量x时,输出\(y=f(x)\)对应{1,2,...,k}中的一个值。例如输入为手写数字的图片,输出为图片中是哪一个数字。
在现实中,输入值中的向量的可能会发生丢失。在输入向量没有缺失的情况下,学习算法只需定义一个从输入向量到输出值的分类函数。在输入向量缺失的情况下,学习算法要定义一组分类函数,其中每一种函数接收一种向量,这个向量对应着输入值所包含所有向量的子集。假如输入包含n个向量,则在输入缺失的情况下,学习算法要定义\(2^n\)个分类函数。
在这类问题中,计算机先根据已有的数据建立回归模型,然后对新的数据预测输出。常见的有线性回归、逻辑回归等。回归问题和分类问题很相似。回归的一个例子是根据现有的房子面积和房价的数据建立模型,然后预测新的房子面积对应的房价。
在这类问题中,计算机接收一些非结构化的数据(图片、视频、音频等),然后将这些数据转录成类散的文本形式。比如在语音识别中,计算机接收一段语音,然后将语音转化为该语音对应的单词并保存在文本中。
在机器翻译中,计算机接收一种语言的符号序列,并将其翻译成另一种语言的符号序列。最近,深度学习已经在这个任务上产生了重要影响。
结构化输出的输出值是一个向量或者包含多个值的数据结构。结构化输出是一个很大的范畴,包含了上面的转录和机器翻译。结构化输出的一个例子是向计算机输入一幅图片,计算机程序输出一段话来描述这幅图片。
在这类问题中,计算机程序在一组事件或对象中进行检查,筛选出异常的对象。比如银行对客户的信用卡进行检查,从而筛选出交易不正常的信用卡。
在这类任务中,机器学习程序生成一些和训练数据相似的新数据。比如在游戏中有很多环境比如树、草需要设计师来绘画,而通过合成和采样,程序可以自动生成这些环境。这其实也是一种结构化输出任务,只是输出不止一种,这样才更自然。比如程序生成的树要有不同形态,才会符合实际。
在这类问题中,输入样本\(x\)缺少一些元素(特征),通过缺失值填补算法来填补缺失值。
假设一个干净的样本为\(x\),\(x\)经噪声污染后变为\(\hat x\),现在输入\(\hat x\),要求程序预测原来的样本\(x\),或者更一般地预测条件概率\(p(x|\hat x)\)。
在这类任务中,机器学习程序根据输入值来估计样本的概率分布,密度估计对应连续型,概率质量函数对应离散型。
我们通过性能度量来衡量机器学习算法的能力。通常性能度量P是特定于系统执行的任务T而言的。
对于分类、转录等任务,我们通过其输出的准确率(accuracy)来衡量算法的好坏。准确率是指模型输出正确结果在所有结果中的比率。与之相对的是错误率(error rate),即输出错误结果所占的样本比率。我们通常把错误率称为0-1损失的期望。在一个特定样本中,如果结果是对的,那么0-1损失是0,如果是错的,则0-1损失是1。对于密度估计这类任务而言,准确率和错误率是没有意义的,我们必须使用不同的性能度量,最常用的方法是输出模型在一些样本的概率对数的平均值。
通常我们会更关注机器学习算法在未观测数据集上的性能,因为这更能体现实际应用的情况。因此,我们使用测试集(test set)数据来评估模型性能,与训练模型使用的训练集数据分开。
根据学习过程中的不同经验,我们可以将机器学习算法分为无监督算法(unsupervised)算法和监督算法(supervised)。
大部分机器学习算法都可以理解为从整个数据集(data set)中获取经验,经验可以近似理解为数据集。数据集是指很多样本的集合,所以有时我们也称样本为数据点(data point)。
无监督学习算法(unsupervised learning algorithm)训练具有很多特征的数据集,然后学习这个数据集中有用的结构性质。监督学习算法(supervised learning algorithm)训练含有很多特征的数据集,不同的是,数据集中的样本都有一个标签(label)或目标(target)。比如学生数据集中的学生样本含有两个特征:身高和体重。在无监督学习中,我们可以通过数据集来学习出概率分布p(x)。假如每一个学生样本都有一个标签来说明学生的胖瘦程度,比如偏胖、正常、偏瘦,则在监督学习中,我们可以对样本进行分类。
大致说来,无监督学习涉及到观察随机向量 x 的好几个样本,试图显式或隐式地学习出概率分布 \(p(x)\),或者是该分布一些有意思的性质;而监督学习包含观察随机向量 x 及其相关联的值或向量 y,然后从 x 预测 y,通常是估计 \(p(y|x)\)。术语监督学习(supervised learning)源自这样一个视角,教员或者老师提供目标 y 给机器学习系统,指导其应该做什么。在无监督学习中,没有教员或者老师,算法必须学会 在没有指导的情况下理解数据。
无监督学习和监督学习之间的界限通常是模糊的。无监督学习算法可以分解为监督学习算法,而监督学习算法也可以通过无监督算法的思想来解决。比如,在概率链式法则下,随机向量\(\rm x∈\mathbb{R}^n\)可以分解为多个概率的乘积:
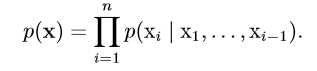
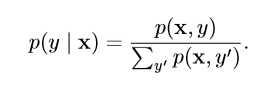
前面我们提过,机器学习算法一般是在整个数据集上获取经验。数据集可以使用设计矩阵(design matrix)来表示。举个例子,学生数据集有100个样本,每个样本有两个特征:身高和体重,则该数据集可以被表示为数据矩阵\(X∈\mathbb{R}^{100×2}\)。其中\(X_{i,}\)表示第i个学生,\(X_{i,1}\)表示第i个学生的身高,\(X_{i,2}\)表示第i个学生的体重,\(i∈[1,100]\)。并不是每个数据集都能对应一个设计矩阵,因为有些数据集中的样本可能具有不同的维度(特征个数不同)。例如,你有不同宽度和高度的照片的集合,那么不同的照片将会包含不同数量的像素,因此不是所有的照片都可以表示成相同长度的向量。在这种情况下,我们不再使用m行设计矩阵,而是使用m个向量的结合:\(\{x^{(1)},x^{(2)},...,x^{(m)}\}\),这意味着样本向量\(x^{(i)}\)和\(x^{(j)}\)可以具有不同的大小。
在监督学习中,样本包含一个标签或目标和一组特征。例如,我们希望使用学习算法从照片中识别对象。我们需要明确哪些对象会出现在每张照片中。我们或许会用数字编码表示,如 0 表示人、1 表示车、2 表示猫等等。通常在处理包含观测特征的设计矩阵 X 的数据集时,我们也会提供一个标签向量 \(y\),其中 \(y_i\) 表示样本 i 的标签。
当然,有时标签可能不止一个数。例如,如果我们想要训练语音模型转录整个句子,那么每个句子样本的标签是一个单词序列。
正如监督学习和无监督学习没有正式的定义,数据集或者经验也没有严格的区分。
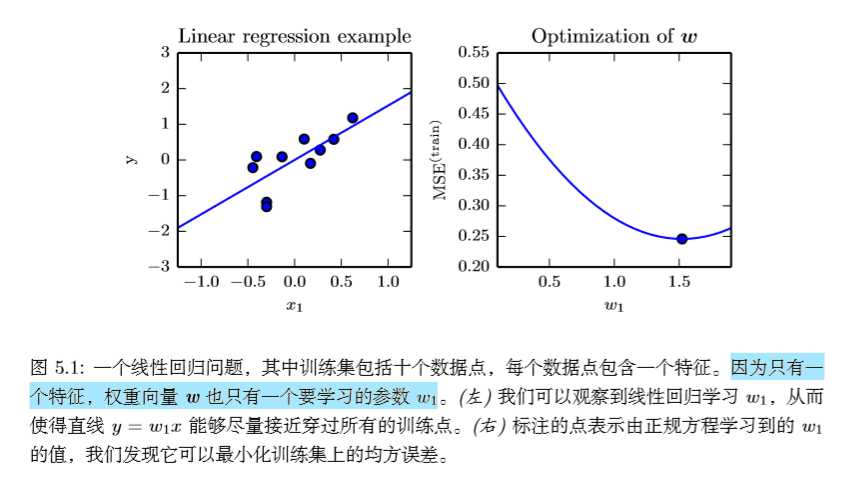
我们可以将机器学习算法定义为通过经验提高计算机程序在某些任务上的性能的算法。为了使定义更清楚一点,下面将介绍一个例子:线性回归(linear regression)。
线性回归解决回归问题。我们目标是建立一个系统,该系统接收输入向量\(x∈\mathbb{R}^n\),然后预测输出标量\(y∈\mathbb{R}\),其中输出是输入的线性函数。我们将预测的输出值记为\(\hat y\),则有:\[\hat y=ω^Tx\]
其中\(ω^T∈\mathbb{R}\)被称为参数向量。参数是控制系统行为的值,由于最后的结果是\(ω\)中的每个元素和\(x\)中的每个元素相乘后相加,所以\(ω_i\)的值决定了\(x_i\)对最后结果的影响,则\(ω\)也可以看作是权重(weight)。
因此,我们可以定义任务T:利用\(\hat y=ω^Tx\)通过输入\(x\)预测输出\(y\)。接下来我们要定义性能度量P。
假设我们有\(m\)个输入样本组成的输入矩阵,这个矩阵不用来训练数据,而是用来评估模型性能,则称该输入矩阵为测试集(test set)。同时,我们还有数据矩阵中每个向量对应的正确输出向量\(y\)(\(y\)也被成为回归目标向量)。我们将输入设计矩阵记为\(X^{(test)}\),回归目标向量记为\(y^{(test)}\)。我们可以使用均方误差来度量模型在测试集上的性能。如果\(\hat y^{(test)}\)表示模型在测试集上的预测值,则均方误差可以表示为:
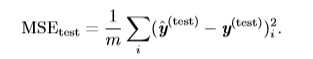
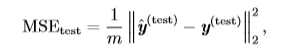
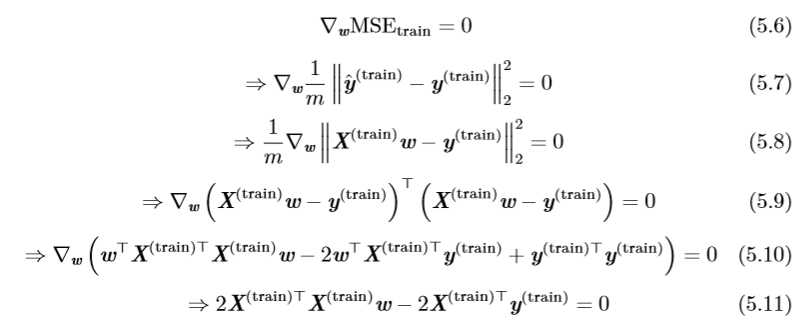
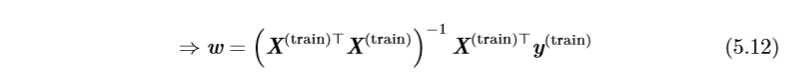
标签:哪些 应该 完全 使用 事件 视频、 test 简单的 技术
原文地址:https://www.cnblogs.com/sench/p/9504701.html