神经网络- 深度学习optimizer的选择

标签：也会   ams   方差   提前   选择   func   targe   一次循环   设定   

optimizer是在训练中，运用到的训练方法，最常用的是梯度下降法，去寻找最优loss，tf中常见的optimizer有：

通过Dr.Sebastian Ruder 的论文An overview of gradient descent optimization algorithms来详细了解一些优化器的选择。

论文地址：https://arxiv.org/pdf/1609.04747.pdf

1. 首先讨论 Batch gradient descent, 公式为： θ = θ ? η · ?θJ(θ)

BDG采用整个训练集来计算cost function对参数的梯度，由于这种方法是在一次更新中，就对整个数据集计算梯度，所以计算起来非常慢，遇到很大量的数据集也会非常棘手，而且不能投入新数据实时更新模型。

for i in range(nb_epochs):
  params_grad = evaluate_gradient(loss_function, data, params)
  params = params - learning_rate * params_grad

2.Stochastic gradient descent, 公式为：θ = θ ? η · ?θJ(θ; x (i) ; y (i) )

和 BGD 的一次用所有数据计算梯度相比，SGD 每次更新时对每个样本进行梯度更新， 对于很大的数据集来说，可能会有相似的样本，这样 BGD 在计算梯度时会出现冗余，而 SGD 一次只进行一次更新，就没有冗余，而且比较快，并且可以新增样本。

for i in range(nb_epochs):
  np.random.shuffle(data)
  for example in data:
    params_grad = evaluate_gradient(loss_function, example, params)
    params = params - learning_rate * params_grad

代码可以看出，在数据集中循环，每次样本做梯度下降更新。

缺点：更新频繁，会造成 cost function 有严重的震荡

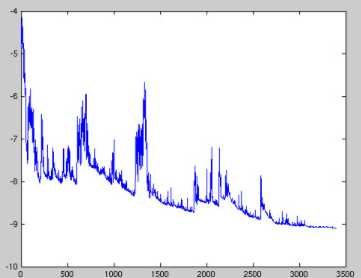
BGD 可以收敛到局部极小值，当然 SGD 的震荡可能会跳到更好的局部极小值处。当我们稍微减小 learning rate，SGD 和 BGD 的收敛性是一样的。

3. Mini-batch gradient descent, 公式：θ = θ ? η · ?θJ(θ; x (i:i+n) ; y (i:i+n) )

MBGD 每一次利用一小批样本，即 n 个样本进行计算， 这样它可以降低参数更新时的方差，收敛更稳定，另一方面可以充分地利用深度学习库中高度优化的矩阵操作来进行更有效的梯度计算。和 SGD 的区别是每一次循环不是作用于每个样本，而是具有 n 个样本的批次。

for i in range(nb_epochs):
  np.random.shuffle(data)
  for batch in get_batches(data, batch_size=50):
    params_grad = evaluate_gradient(loss_function, batch, params)
    params = params - learning_rate * params_grad

batch_size通常为：50～256。

缺点: 

不过 Mini-batch gradient descent 不能保证很好的收敛性：

1. learning rate 如果选择的太小，收敛速度会很慢，如果太大，loss function 就会在极小值处不停地震荡甚至偏离。（有一种措施是先设定大一点的学习率，当两次迭代之间的变化低于某个阈值后，就减小 learning rate，不过这个阈值的设定需要提前写好，这样的话就不能够适应数据集的特点）

2. 此外，这种方法是对所有参数更新时应用同样的 learning rate，如果我们的数据是稀疏的，我们更希望对出现频率低的特征进行大一点的更新。

3. 另外，对于非凸函数，还要避免陷于局部极小值处，或者鞍点处，因为鞍点周围的error 是一样的，所有维度的梯度都接近于0，SGD 很容易被困在这里。

函数凹凸性：

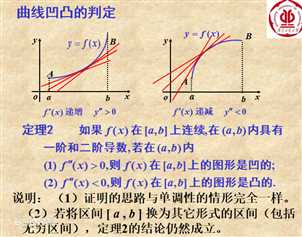
鞍点：一个光滑函数的鞍点邻域的曲线，曲面，或超曲面，都位于这点的切线的不同边。

神经网络- 深度学习optimizer的选择

标签：也会   ams   方差   提前   选择   func   targe   一次循环   设定   

原文地址：https://www.cnblogs.com/ChrisInsistPy/p/9510650.html