标签：span 斐波那契数列 生成 const image 重点 公式 style src
方法一 用数组开，一般开到1e7，1e8 左右的数组就是极限了 对时间也是挑战
#include<bits/stdc++.h> using namespace std; const int maxn=1e8+10; int a[maxn]; int32_t main() { a[1]=1; a[2]=1; for(int i=3;i<maxn;i++) a[i]=a[i-1]%10000000+a[i-2]%100000000; cout<<a[maxn-1]<<endl; }
方法二 求第多少个斐波那契数 时间还是个问题
#include<bits/stdc++.h> using namespace std; const int maxn=1e8+10; int32_t main() { int x; x=1000; if(x==1) cout<<1<<endl; if(x==2) cout<<1<<endl; if(x>3) { int a=1; int b=1; int c=0; for(int i=3;i<=x;i++) { c=(a+b)%100000000; a=b%100000000; b=c; } cout<<c<<endl; } }
方法三
通项公式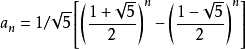 
a[n]=1/sqrt(5) ( ((1+sqrt(5))/2 )^n-((1-sqrt(5))/2)^n )；
这不是重点 重要的是 矩阵 求斐波那契数列
不是很会矩阵 推荐这个博客 https://blog.csdn.net/flyfish1986/article/details/48014523
标签：span 斐波那契数列 生成 const image 重点 公式 style src
原文地址：https://www.cnblogs.com/Andromeda-Galaxy/p/9516915.html
